Confidence levels, significance levels and critical values

Introduction to Confidence Levels, Significance Levels, and Critical Values

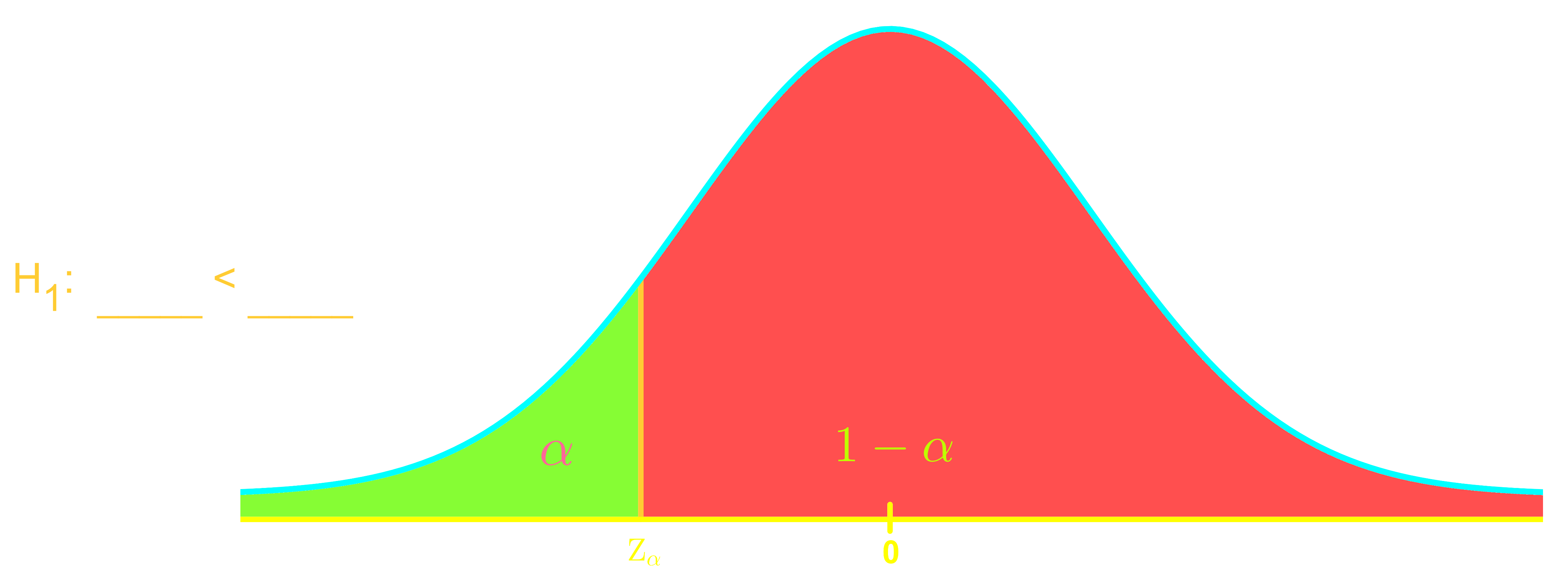
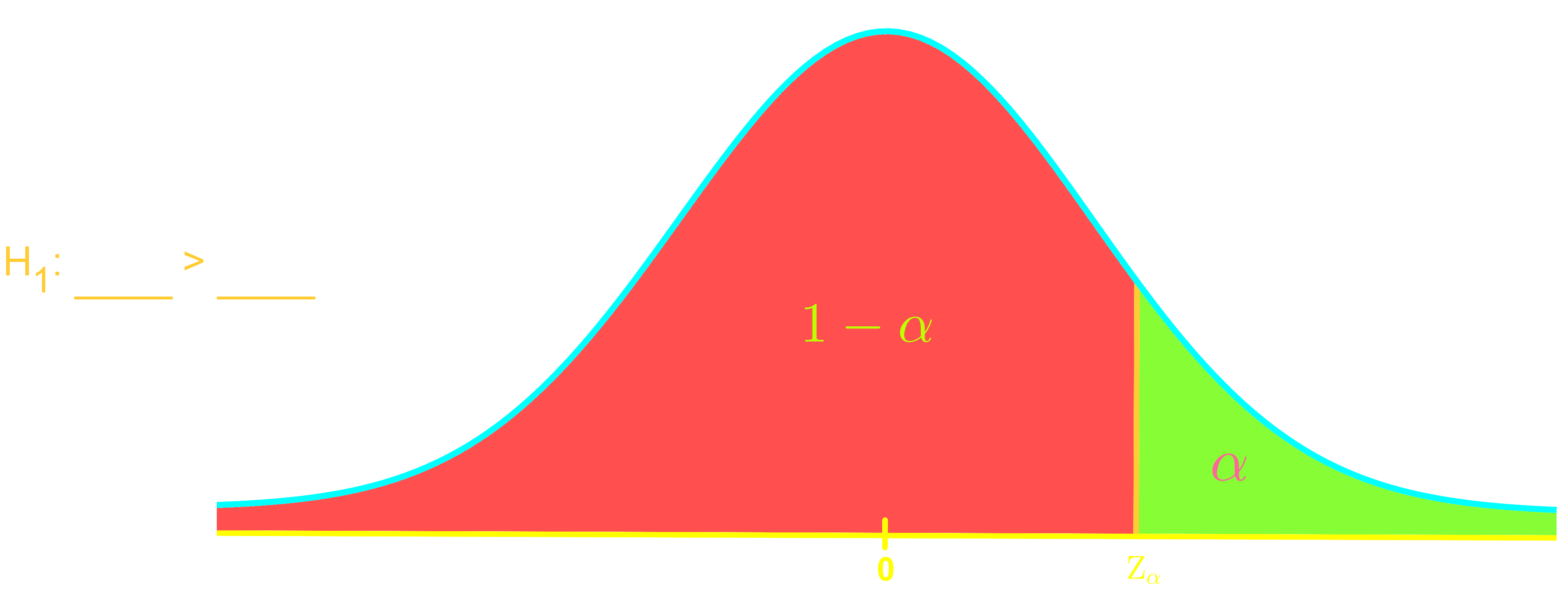
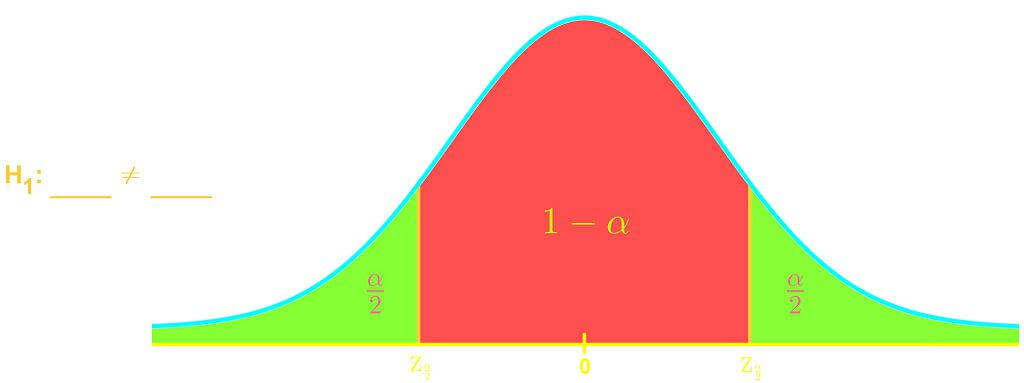
Welcome to our exploration of key concepts in hypothesis testing! In this section, we'll dive into confidence levels, significance levels, and critical values. These fundamental ideas form the backbone of statistical analysis. Our introduction video is a great starting point to grasp these concepts visually. Confidence levels tell us how sure we are about our results, typically expressed as percentages like 95% or 99%. Significance levels, often denoted as α (alpha), represent the probability of rejecting a true null hypothesis. Critical values are the boundaries that help us make decisions in hypothesis tests. They're closely linked to both confidence and significance levels. Understanding these concepts is crucial for interpreting statistical results accurately. As we progress, you'll see how these elements work together in hypothesis testing, allowing you to make informed decisions based on data. Remember, mastering these ideas takes practice, so don't hesitate to review the video and ask questions!

Understanding Confidence Levels and Significance Levels

In the world of statistics and hypothesis testing, two crucial concepts often come into play: confidence levels and significance levels. These two concepts are closely related and play a vital role in determining the reliability of statistical results. Let's dive into their relationship and explore how they impact our understanding of data.

Confidence levels and significance levels are complementary to each other, always summing up to 1 (or 100%). This relationship is fundamental to understanding how we interpret statistical results. The confidence interval represents the probability that a population parameter falls within a specific range, known as the confidence interval. On the other hand, the significance level, often denoted as α (alpha), represents the probability of rejecting the null hypothesis when it is actually true (Type I error).

Let's look at some common confidence levels and their corresponding significance levels:

• 90% confidence level corresponds to a 0.10 significance level
• 95% confidence level corresponds to a 0.05 significance level
• 99% confidence level corresponds to a 0.01 significance level

To illustrate, if we choose a 95% confidence level, we're essentially saying that we're 95% confident that our results are accurate. This leaves a 5% chance of error, which is our significance level. In other words, what is the confidence level if α = 0.10? The answer is 90%, as 0.90 + 0.10 = 1.

The choice of confidence level (and consequently, the significance level) depends on the nature of the study and the potential consequences of making an error. In many fields, a 95% confidence level (0.05 significance level) is considered standard. However, in some cases where more stringent evidence is required, such as in medical research or high-stakes decision-making, a 99% confidence level (0.01 significance level) might be preferred.

Let's consider an example to understand how these concepts apply in practice. Imagine we're conducting a study on the effectiveness of a new medication. If we use a 95% confidence level, we're saying that if we repeated this study many times, 95% of the time, our results would fall within the calculated confidence interval. The 0.05 significance level means we have a 5% chance of concluding the medication is effective when it actually isn't (Type I error).

When we talk about a 0.01 significance level confidence interval, we're referring to a 99% confidence level. This means we're setting a higher bar for declaring statistical significance. It reduces the chance of falsely rejecting the null hypothesis but also makes it harder to detect true effects.

On the other hand, a 0.10 significance level confidence interval corresponds to a 90% confidence level. This is less stringent and might be used in exploratory research or when the consequences of a Type I error are less severe.

It's important to note that while a higher confidence level (and lower significance level) might seem always preferable, it comes with trade-offs. A 99% confidence interval will be wider than a 95% confidence interval, providing less precise estimates. Additionally, it increases the risk of Type II errors (failing to reject a false null hypothesis).

In hypothesis testing, the significance level is crucial in determining whether we reject or fail to reject the null hypothesis. If our p-value (the probability of obtaining our results if the null hypothesis is true) is less than our chosen significance level, we reject the null hypothesis. For instance, with a 0.05 significance level, a p-value of 0.03 would lead to rejecting the null hypothesis, while a p-value of 0.07 would not.

Understanding the relationship between confidence levels and significance levels is essential for interpreting statistical results accurately. Whether you're analyzing market trends, conducting scientific research, or making data-driven decisions in business, these concepts provide a framework for assessing the reliability of your findings and the strength of your conclusions.

Remember, the choice between different confidence levels (90%, 95%, 99%) and their corresponding significance levels

The Standard Normal Distribution and Critical Values

The standard normal distribution, often referred to as the z-distribution, is a fundamental concept in statistics that plays a crucial role in hypothesis testing and confidence interval estimation. This bell-shaped curve is symmetrical around its mean of zero and has a standard deviation of one. Understanding this distribution is essential for interpreting z-scores, determining critical values, and making statistical inferences.

At the heart of the standard normal distribution is its characteristic shape. The curve is highest at the center (mean) and tapers off symmetrically on both sides, forming the familiar bell curve. This shape illustrates that values closer to the mean are more probable, while extreme values are less likely to occur. The area under the entire curve always equals 1, representing 100% of the data.

Confidence levels and significance levels are closely tied to the standard normal distribution. A confidence level, typically expressed as a percentage (e.g., 95%), represents the probability that a population parameter falls within a specific interval. On the other hand, the significance level (α) is the probability of rejecting the null hypothesis when it's actually true. It's often set at 0.05 or 5%.

Critical values are pivotal points on the standard normal distribution that separate the rejection region from the fail to reject region. These values are determined by the chosen significance level and are typically denoted as z-scores. For a two-tailed test with a 5% significance level, the critical z-values are -1.96 and 1.96. This means that 95% of the data falls between these two points, with 2.5% in each tail representing the rejection regions.

To visualize this, imagine the standard normal distribution curve with the following regions labeled:

• The central area between -1.96 and 1.96, representing 95% of the data (fail to reject region)
• The two tail areas beyond -1.96 and 1.96, each representing 2.5% of the data (rejection regions)

Determining critical values involves using z-score tables or statistical software. For a given significance level, you can find the corresponding z-score that leaves that percentage in the tail(s) of the distribution. For example, a 99% confidence level corresponds to a z-score of approximately 2.58, meaning 0.5% of the data lies beyond each of these points in the tails.

Let's consider a practical example to illustrate these concepts. Suppose you're conducting a study on the average height of adults in a population. You collect a sample and want to construct a 95% confidence interval for the true population mean. Using the standard normal distribution, you would use the critical z-value of 1.96 to calculate the margin of error and establish your confidence interval.

The z-score is a standardized measure that tells you how many standard deviations an observation is from the mean. For instance, a z-score of 2 indicates that a value is two standard deviations above the mean. This standardization allows for easy comparison across different datasets and is crucial for interpreting results in the context of the standard normal distribution.

When conducting hypothesis tests, the critical values serve as decision boundaries. If your test statistic falls within the rejection region (beyond the critical values), you reject the null hypothesis. Otherwise, you fail to reject it. This process is fundamental to statistical inference and helps researchers make informed decisions based on their data.

It's important to note that while the standard normal distribution is widely used, it's an idealized model. Real-world data may not always perfectly fit this distribution. However, thanks to the Central Limit Theorem, many sampling distributions of means approximate the normal distribution, making it a powerful tool in statistical analysis.

In conclusion, the standard normal distribution provides a framework for understanding probability, making statistical inferences, and interpreting data. By grasping concepts like critical values, z-scores, and the relationships between different regions of the curve, you'll be well-equipped to apply statistical techniques in various fields, from scientific research to business analytics. Remember, practice and application are key to fully appreciating the power and utility of the standard normal distribution in statistical analysis.

Left-Tail, Right-Tail, and Two-Tail Tests

In the world of hypothesis testing, understanding the differences between left-tail, right-tail, and two-tail tests is crucial for making accurate statistical inferences. These tests are essential tools in determining whether to reject or fail to reject a null hypothesis based on sample data. Let's dive into each type of test and explore how to choose the appropriate one for your analysis.

Left-tail tests, also known as lower-tail tests, are used when we're interested in determining if a population parameter is less than a specified value. The alternative hypothesis in a left-tail test suggests that the true population parameter is lower than the value stated in the null hypothesis. For example, if we're testing whether a new manufacturing process reduces production time, we might use a left-tail test to see if the mean production time is less than the current standard.

Right-tail tests, or upper-tail tests, are the opposite of left-tail tests. They're employed when we want to investigate if a population parameter is greater than a specified value. The alternative hypothesis in a right-tail test proposes that the true population parameter exceeds the value stated in the null hypothesis. For instance, if we're examining whether a new fertilizer increases crop yield, a right-tail test would be appropriate to determine if the mean yield is higher than the current average.

Two-tail tests, also called two-sided tests, are used when we're interested in any deviation from a specified value, regardless of direction. The alternative hypothesis in a two-tail test suggests that the true population parameter is either less than or greater than the value stated in the null hypothesis. This type of test is useful when we want to detect changes in either direction. For example, if we're testing whether a new teaching method affects test scores, we might use a two-tail test to see if the scores are significantly different (either higher or lower) from the current average.

Determining which test to use is primarily based on the alternative hypothesis you want to investigate. If you're looking for a decrease in a parameter, use a left-tail test. If you're searching for an increase, opt for a right-tail test. When you're interested in any change, regardless of direction, a two-tail test is the way to go. It's crucial to decide on the appropriate test before collecting data to avoid bias in your analysis.

Let's look at some examples to illustrate each type of test:

1. Left-tail test example: A company claims that its new energy-saving lightbulbs last an average of 1000 hours. You suspect they might not last as long. Your null hypothesis (H0) would be that the mean lifespan is 1000 hours, and your alternative hypothesis (Ha) would be that it's less than 1000 hours. You would use a left-tail test to analyze your sample data.

2. Right-tail test example: A sports drink manufacturer asserts that their product improves endurance by increasing running distance. The average runner completes 5 miles. Your null hypothesis (H0) would be that the mean distance is 5 miles, and your alternative hypothesis (Ha) would be that it's greater than 5 miles. A right-tail test would be appropriate here.

3. Two-tail test example: A researcher wants to know if a new medication affects patients' heart rates. The current average resting heart rate is 70 beats per minute. The null hypothesis (H0) would be that the mean heart rate is 70 bpm, and the alternative hypothesis (Ha) would be that it's not equal to 70 bpm. A two-tail test would be used to detect changes in either direction.

Interpreting the results of these tests involves comparing the calculated test statistic to the critical values or examining the p-value. For left-tail and right-tail tests, you typically have one critical value to compare against. If the test statistic falls in the rejection region (beyond the critical value), you reject the null hypothesis. For two-tail tests, you have two critical values, creating rejection regions on both tails of the distribution.

When using p-values, you compare the calculated p-value to your chosen significance level (often denoted as α). If the p-value is less than α, you reject the null hypothesis. For two-tail tests, remember

Calculating and Interpreting Critical Values

Understanding how to calculate and interpret critical values is essential for conducting hypothesis tests and constructing confidence intervals. This guide will walk you through the process step-by-step, helping you master this crucial statistical skill.

Step 1: Determine the Confidence Level and Test Type

Before calculating critical values, you need to know your desired confidence level (commonly 90%, 95%, or 99%) and whether you're conducting a one-tailed or two-tailed test. This information is crucial for finding the correct critical value.

Step 2: Identify the Appropriate Distribution

Most hypothesis tests use either the z-distribution (for large samples or known population standard deviation) or the t-distribution (for smaller samples with unknown population standard deviation). Ensure you're using the correct distribution for your test.

Step 3: Use a Z-Table or Calculator

For z-tests, you'll need to use a z-table or an online z-score calculator. Here's how to use a z-table:

1. For a two-tailed test, find the area in the body of the table that corresponds to half of your confidence level (e.g., 0.975 for a 95% confidence level).
2. Look up the corresponding z-score in the left column and top row of the table.
3. For a one-tailed test, use the full confidence level (e.g., 0.95 for 95% confidence).

Step 4: Calculate Critical Values for T-Tests

For t-tests, you'll need to use a t-table or t-distribution calculator. The process is similar to using a z-table, but you'll also need to consider the degrees of freedom (df) for your test.

1. Determine your degrees of freedom (usually n-1, where n is your sample size).
2. Find the column in the t-table that corresponds to your confidence level.
3. Locate the critical value where your df row intersects with the confidence level column.

Step 5: Interpret the Critical Values

Once you've found your critical value(s), it's time to interpret them in the context of your hypothesis test. Here's what they mean:

• For a two-tailed test, you'll have two critical values (positive and negative). Your test statistic must fall outside these values to reject the null hypothesis.
• For a one-tailed test, you'll have one critical value. Your test statistic must be more extreme than this value in the direction of your alternative hypothesis to reject the null.

Example: Two-Tailed Z-Test at 95% Confidence

Let's say you're conducting a two-tailed z-test with a 95% confidence level. Here's how to find and interpret the critical values:

1. For a 95% confidence level in a two-tailed test, we look for 0.975 in the z-table (because 0.95 / 2 = 0.475, and 1 - 0.475 = 0.975).
2. The corresponding z-score is approximately 1.96.
3. Our critical values are therefore -1.96 and +1.96.
4. Interpretation: If our calculated test statistic falls below -1.96 or above +1.96, we reject the null hypothesis.

Example: One-Tailed T-Test at 90% Confidence

Now, let's consider a one-tailed t-test with a 90% confidence level and 20 degrees of freedom:

1. Using a t-table,

   Practical Applications of Confidence Levels and Significance Levels

   Confidence levels and significance levels are crucial statistical concepts that play a vital role in various fields, from scientific research to quality control and market research. These concepts help professionals make informed decisions based on data analysis. Let's explore some real-world applications of these statistical tools and how they impact decision-making processes.

   In scientific research, confidence levels and significance levels are fundamental to hypothesis testing and drawing reliable conclusions. For instance, when testing a new drug's effectiveness, researchers might set a confidence level of 95% and a significance level of 0.05. This means they want to be 95% certain that their results are not due to chance, and they're willing to accept a 5% risk of incorrectly rejecting the null hypothesis. If the study's p-value is less than 0.05, researchers can confidently claim that the drug has a statistically significant effect.

   Quality control in manufacturing is another area where these concepts are widely applied. Imagine a company producing electronic components with a target defect rate of 1%. They might use a 99% confidence level to ensure their sampling process accurately reflects the entire production. If their quality control tests show a defect rate significantly higher than 1% (based on the chosen significance level), they can quickly identify and address production issues, maintaining high product standards.

   Market research heavily relies on confidence and significance levels to make business decisions. For example, a company launching a new product might conduct a survey to gauge consumer interest. With a 90% confidence level and a margin of error of 3%, they can estimate the percentage of their target market likely to purchase the product. If the survey results show a significant interest (based on the predetermined significance level), the company may proceed with the product launch, confident in their market analysis.

   In the field of environmental science, researchers often use these statistical tools to assess the impact of human activities on ecosystems. For instance, when studying the effects of a new industrial plant on local air quality, scientists might set a 99% confidence level and a significance level of 0.01. If their analysis shows a statistically significant increase in air pollutants after the plant's operation began, policymakers can use this information to implement stricter environmental regulations.

   The healthcare industry also benefits from the application of confidence and significance levels. When evaluating the effectiveness of a new treatment or medical procedure, doctors and researchers typically use a 95% confidence level. This means they can be 95% certain that the observed effects are due to the treatment and not random chance. If the results are statistically significant, it can lead to the approval of new treatments, potentially improving patient outcomes.

   In the realm of public opinion polling, such as political surveys, confidence levels and significance levels are crucial for accurate reporting. A poll might use a 95% confidence level with a margin of error of 3%. This allows pollsters to make statements like, "We are 95% confident that the true population value falls within 3 percentage points of our sample estimate." Understanding these concepts helps the public interpret poll results more accurately and avoid drawing hasty conclusions from small differences in numbers.

   Financial analysts use these statistical tools to assess investment risks and make predictions about market trends. For example, when analyzing historical stock performance to predict future returns, an analyst might use a 90% confidence level. This provides a range of likely outcomes, helping investors make more informed decisions about their portfolios. If the analysis shows a statistically significant trend, it can influence investment strategies and risk management approaches.

   In conclusion, confidence levels and significance levels are indispensable tools across various fields, enabling professionals to make data-driven decisions with a clear understanding of the associated uncertainties. Whether it's in scientific research, quality control, market research, or any other data-intensive field, these concepts provide a framework for interpreting results and assessing their reliability. By understanding and applying these statistical principles, professionals can enhance the accuracy of their analyses, make more informed decisions, and communicate their findings with greater clarity and confidence.

   Conclusion: Mastering Confidence Levels, Significance Levels, and Critical Values

   In this article, we've explored the crucial concepts of confidence levels, significance levels, and critical values in statistical analysis and hypothesis testing. Understanding these elements is essential for making informed decisions based on data. Confidence levels help determine the reliability of our estimates, while significance levels guide us in assessing the strength of evidence against null hypotheses. Critical values serve as important thresholds in hypothesis testing, enabling us to draw meaningful conclusions. To solidify your grasp of these concepts, we encourage you to review the introductory video, which provides a comprehensive overview. By mastering these fundamental principles, you'll enhance your ability to interpret statistical results accurately and make data-driven decisions with confidence. We invite you to delve deeper into this topic by exploring related resources, practicing with real-world datasets, and engaging in discussions with fellow statisticians. Your journey towards statistical proficiency begins here embrace the power of these tools to unlock valuable insights in your data analysis endeavors.