Slope Intercept Form y = mx + b
What is Slope Intercept Form
Slope intercept form is one of the three forms we can use to express a straight line. The other forms are called point slope form and standard form, but we will mostly be using slope intercept form in this section. Using slope intercept form, we express the equation of a line to be:
You may know and to be coordinates of a point on a graph, but what are and ?
What is b in y=mx+b?
The letter b is a number that represents when the line touches the y-axis. We also refer to this as the "y-intercept". For example, let's draw a straight line on the coordinate plane.
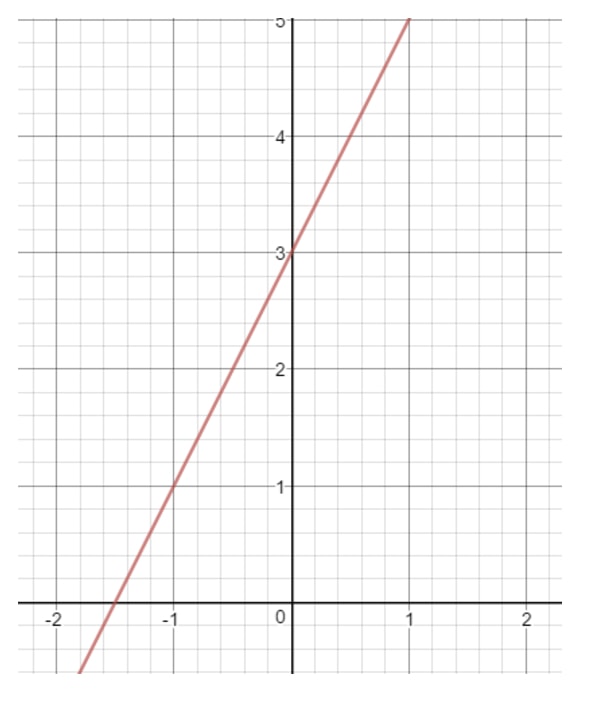
If you were to look closely at the y-axis, the straight line touches the y-axis at a specific place. Where is that place? That would be the number 3 because that is where the y-axis and the line intersect. This means we can conclude that b = 3.
What is m in slope intercept form?
The letter m is a number that represents the slope of the line. Some people refer to the slope as rise over run. Recall that if we have two points, then we are able to find the slope of the two points by using the slope formula
The same idea works here. If we take any two points on a straight line, then we can find the slope of the line using the above formula! For example, let's use this line.
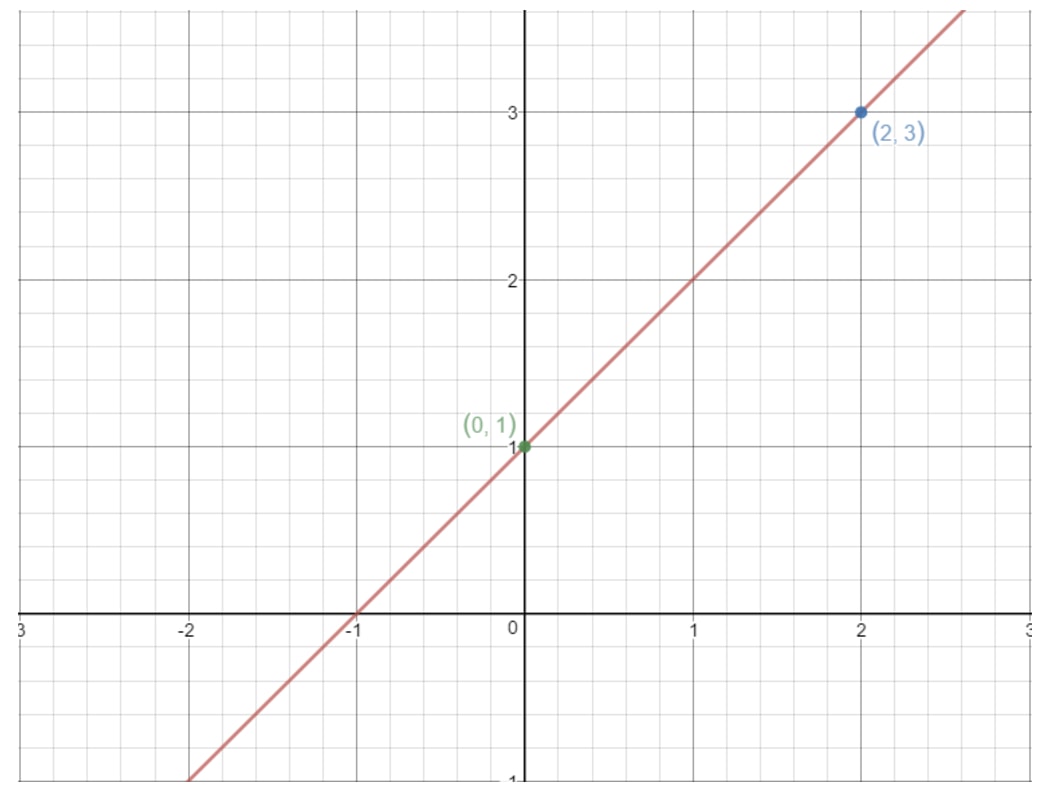
Notice the points (2, 3) and (0, 1) are on this graph. So why don't we use these two points to find the slope of the line? Using the formula, we would get:
That means the slope of this line is !
You can also use the rise over run concept here as well. To go from the point (0, 1) to (2, 3), we have to go units right and units up. That means rise is and run is , thus .
The special thing about slopes is that we can use any two points on the line to find it. So if you took two different points on this line, you would still get that the slope is .
How to write an equation in slope intercept form?
You may know what the slope intercept form looks like, but half the time you will be given equations that are not in that form. So it is your job to turn it into slope-intercept form. How do we do that? The goal is to always isolate the term. For example, let's say you're given the equation
To isolate , we move the to the right side of the equation
Now the is in the way of , so we are going to get rid of it by dividing both sides of the equation by .
Since is isolated, you can see that it is in slope intercept form where , and .
Now that we know the y intercept and slope really well, why don't we look at specific questions about finding them!
How to find y intercept?
Question 1: Using the linear equation , find y intercept.
Notice here that the equation is already in the slope intercept form . We just need to find out what is. We can see that , so the y intercept is .
Let's do a slightly harder question.
Question 2: Determine the y-intercept of
Now this linear equation is not in slope intercept form, so we have to change it into that form first. Our goal is to isolate in this equation.
See that if we move the to the right side of equation, we will have:
Now dividing both sides by , we will get:
Now switching the positions of the two terms gives us:
We can clearly see that the equation is in slope intercept form . Just by looking at the equation, we can see that , and so the y intercept is . Let's do another similar question.
Question 3: Determine the y intercept of .
This may look a bit weird because there is no term, but our goal remains the same. We are going to isolate .
Moving the to the right side of the equation gives us:
Dividing both sides of the equation by gives us
Now this may not look like it, but the equation is in slope intercept form. It's just that , so the entire term has disappeared. Just rewrite the equation as
From observing, you can tell that , and so the y intercept is . Let's do one more question.
Question 4: Determine (if possible) the y intercept of .
This one is interesting because the equation has no term. So how are we supposed to put it in slope intercept form? Well, the only thing we can do right now is isolate for , so let's try that for now.
Moving the to the right hand side of equation we have:
Dividing both sides of the equation gives:
Now we are going to draw this on a graph. Notice that in this equation, is forced to be and cannot be anything else. However, it doesn't say anything about , so can be anything it likes. If we were to write a table of values, we get:
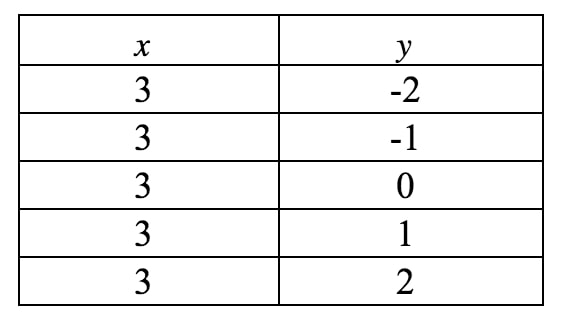
If we plot these points on a coordinate plane and draw the line, we have:
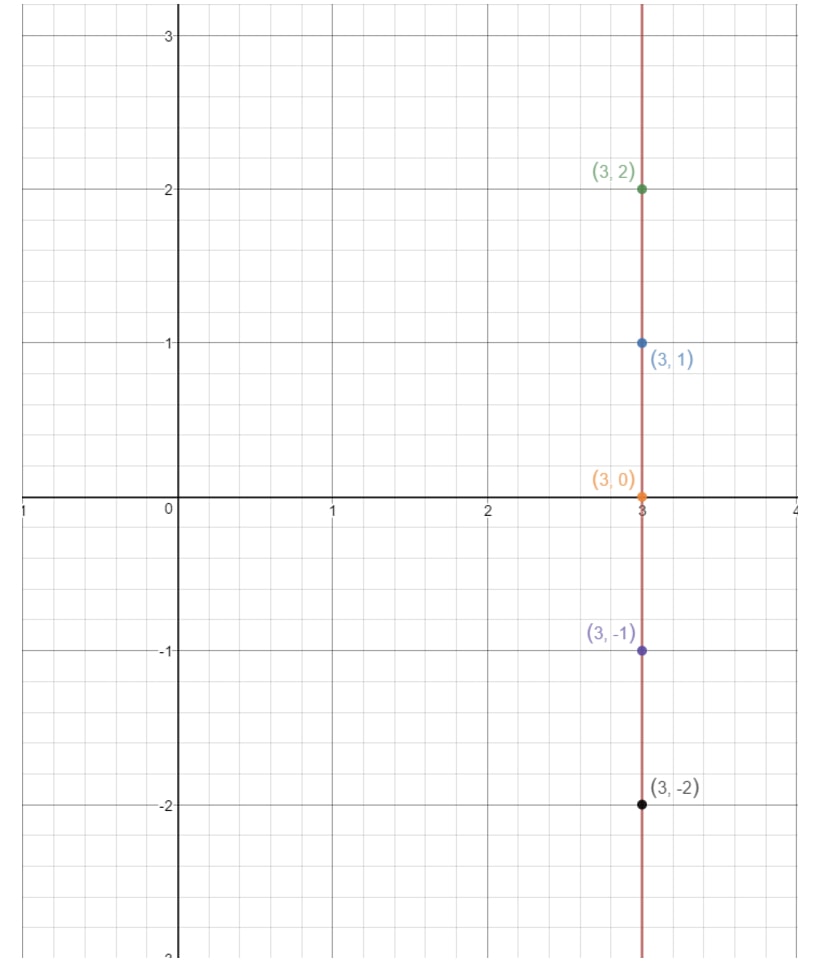
Notice how the line never touches the y-axis. This means the equation does not have a y intercept. Now that we covered all the cases of finding the y intercept, let's look at questions which ask us to find the slope!
How to find the slope of an equation?
Question 5: Find the slope of
Notice here that this is in the slope intercept form , so by observing, we already know that . Hence, the slope is !
Question 6: Determine the slope of the linear equation
As you can see, the equation is not in slope intercept form, so we have to convert it into that form first. Our goal is to isolate .
Moving to the right side of the equation gives:
Dividing both sides by gives:
Notice that this is actually in slope intercept form . It's just that the y intercept in this case is , and is the same as . So we can rewrite the equation to:
Now by observing, we see that . Since is the slope, then the slope must be . Let's do a slightly harder one
Question 7: Determine the slope of
Again, this is a little weird because we have no term. However, our goal to isolate stays the same.
Moving to the right side of the equation we have:
Dividing both sides of the equation by gives:
See here that it is now in slope intercept form, except the term is hidden because . So we can rewrite our equation as:
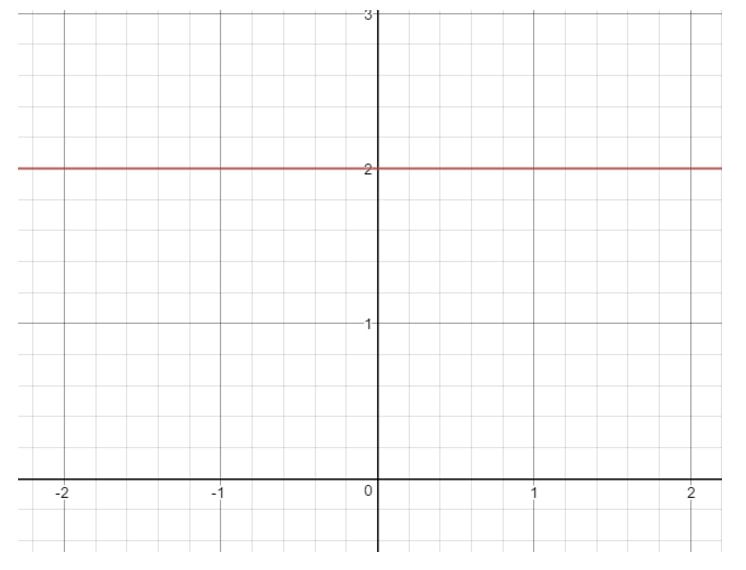
Since , then we have a zero slope. If you are wondering what a line with slope looks like, then here is a graph for you to see.
Question 8: Find (if possible) the slope of the linear equation
In this case, cannot be isolated because there is no term. So the only thing we can do is to isolate .
Moving to the right side of the equation gives:
Dividing both sides by , we get:
This is still not in slope intercept form, so our only hope of attaining the slope is to draw a graph of this line. Again, we see that is always forced to be , but can be anything it likes because there is no term. If we were to write a table of values, we get:
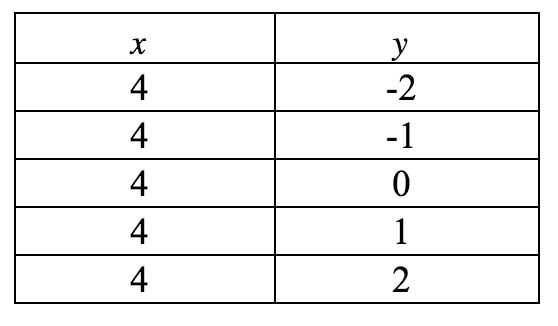
If we plot these points on a coordinate plane and draw the line, we have:
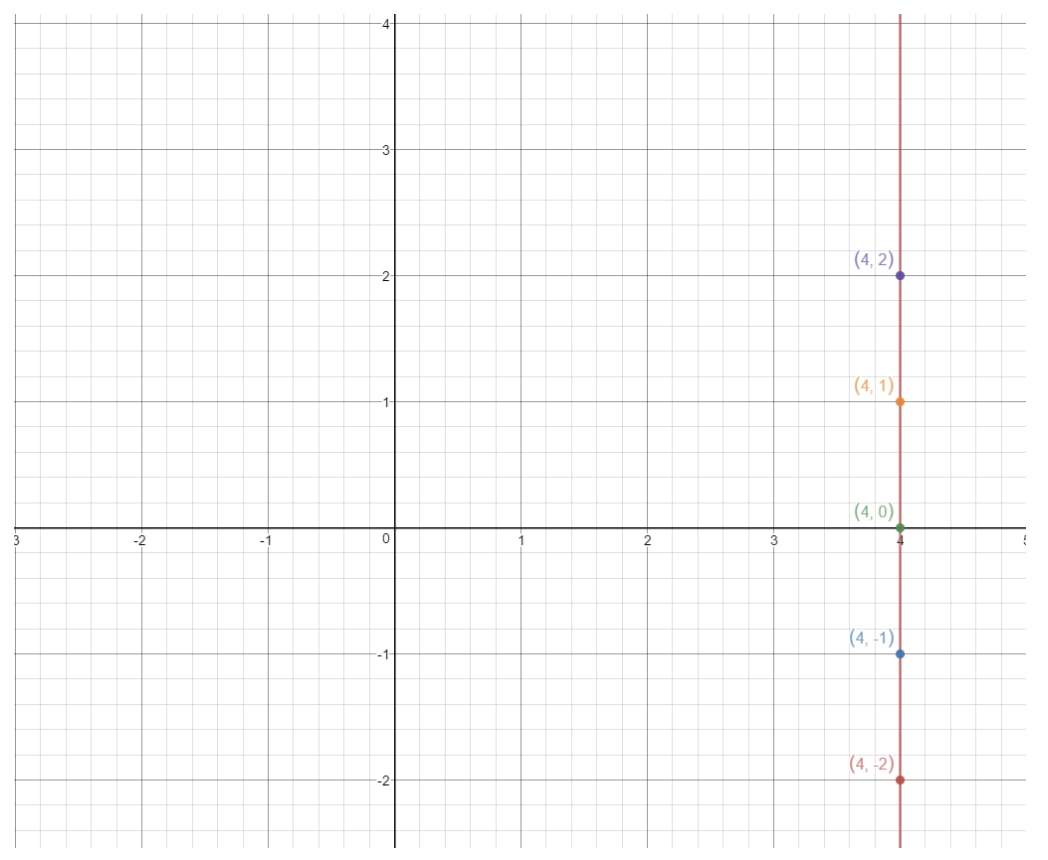
This is a vertical line. So what is the slope of a vertical line? Let's try to figure that out by finding the rise and the run. See how this line is always rising infinitely, but there is no run whatsoever. So that means run is . So if we calculate the slope, then we will get:
We cannot divide by , so we actually have an undefined slope.
What is an undefined slope?
An undefined slope is a slope that goes straight up in the graph. As seen in the graph above, the slope rises infinitely and has no run. As a result, we get an undefined slope because we cannot divide by .
In general, we always get an undefined slope whenever we get a straight vertical line!
Let's look at some other unique questions!
Finding equation from one point
Question 9: A point (2, 6) passes through an equation of . Find "".
Notice here that (2, 6) is a coordinate that tells us when , then . So to solve for , we simply plug the and values into the equation.
Isolating and solving for gives:
Recall that is also known as the y-intercept, so the y intercept is as well!
Finding slope from two points
Question 10: Given two points (6, 1) and (-10, 9), find the slope of the line.
Recall that to find the slope of the line, we use the slope equation
Hence using this formula gives us:
What if we are supposed to find the entire equation of a line instead?
Equation of a line given two points
Question 11: Given two points (-6, 1) and (2, 6), find the slope intercept form equation.
We are basically trying to find the equation in the form of . In order to do this, we need to look for and .
Recall that to find , we use the slope equation
Hence using this formula gives us:
So now we have the equation
Now we have to look for . To solve , we pick either of the given points and plug it into the equation. We can do that because both points lie on the line, and any points on the line would satisfy the equation. Let's use the point (2, 6). See that:
Isolating gives:
Putting this in decimal form, we get that . Hence, our slope intercept form equation is:
The last thing to cover in this section is to find the domain and range of a line.
How to find domain and range?
To find the domain of a line, we are basically asking ourselves this question: what can be? If can be those values, then we add them into the domain.
The same thing goes for range. What can be? If can be those values, then we add them in the range. Let's do an example.
Question 12: Find the domain and range of the equation .
Notice that if we draw the graph of this line, then we will get:
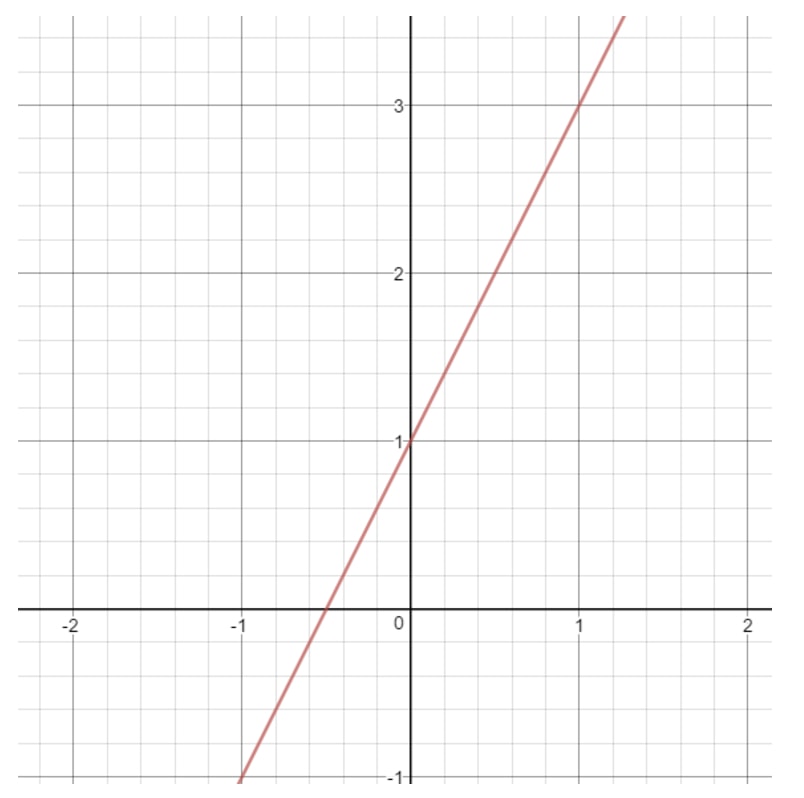
What can be in this line? Notice that can be anything because with any value, we can get a point that is on the line. The same goes for y. We can always pick a value that gives us a point on a line. So we say that
where R means "all real numbers". Let's do a harder one.
Question 13: Find the domain and range of the equation .
Now if we draw this line on a graph, we will get:
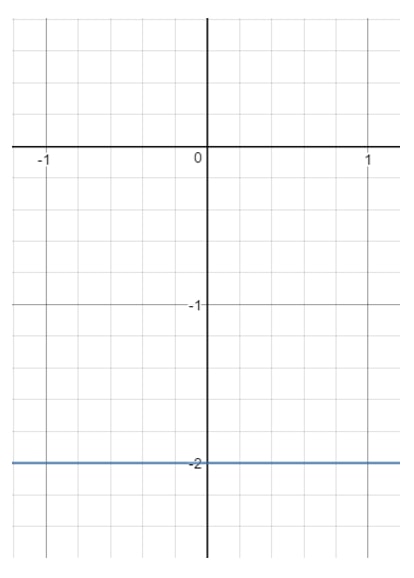
Notice that can be anything because with any value, we can get a point that is on the line as long as . However, look at . You see that is forced to and cannot be anything else. The moment you pick another value (like ), then that point is going to be out of the line. So that means:
Question 14: Find the domain and range of the equation .
Now if we draw this line on a graph, we will get:
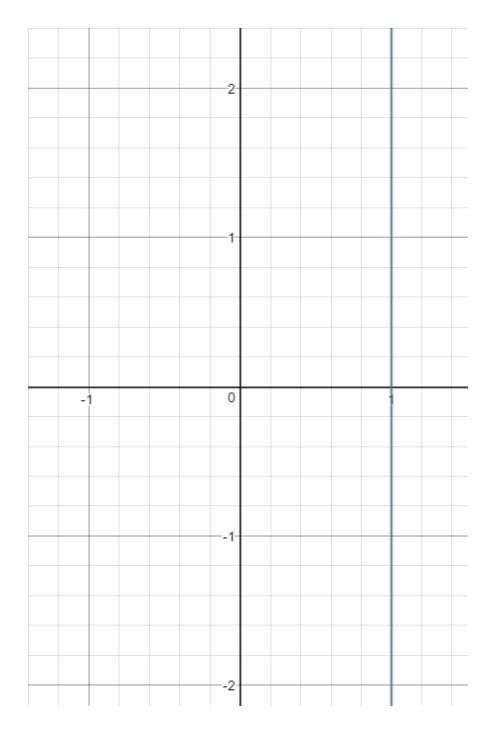
You see that is forced to and cannot be anything else. The moment you pick another value (like ), then that point is going to be out of the line.However, look at . Notice that can be anything because with any value, we can get a point that is on the line as long as
So that means:
If you had a lot of problems drawing the graphs to obtain the domain and range, I recommend you use this calculator.
https://www.desmos.com/calculator/2rnqgoa6a4It teaches you how to graph a linear equation. All you have to do is type the values of and in. Then it will automatically draw the line for you! This is also useful when you are trying to find the slope intercept form.