Mastering Linear-Quadratic Systems: Your Key to Advanced Problem Solving

Dive into the world of linear-quadratic systems. Learn powerful techniques to solve complex equations, visualize solutions graphically, and apply your skills to real-world scenarios. Elevate your math prowess today!

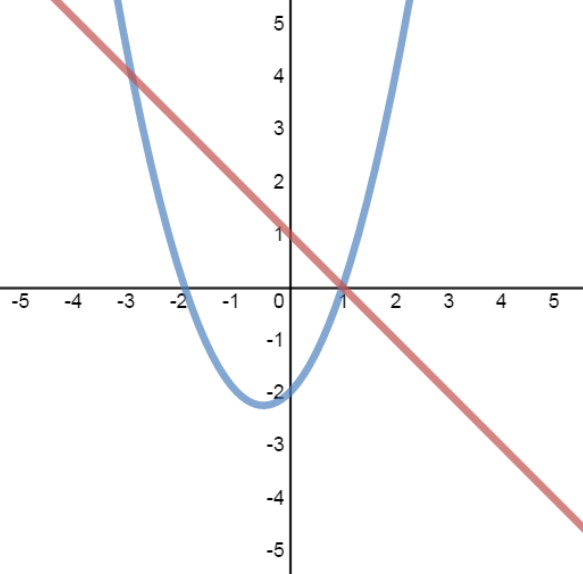
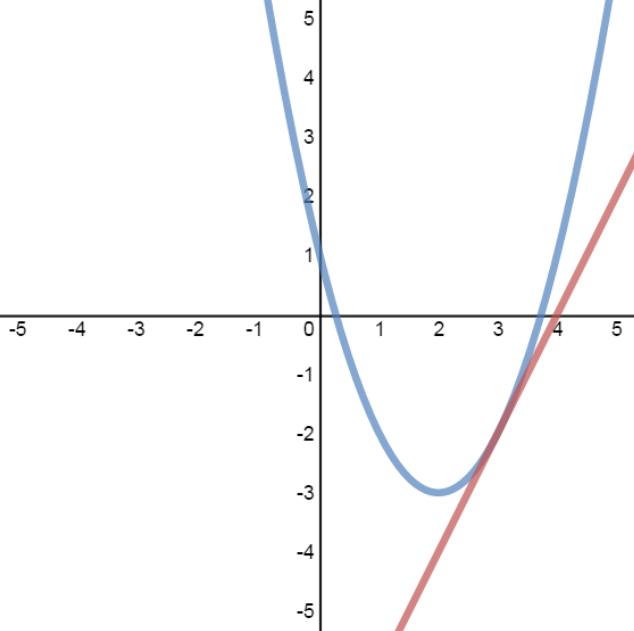
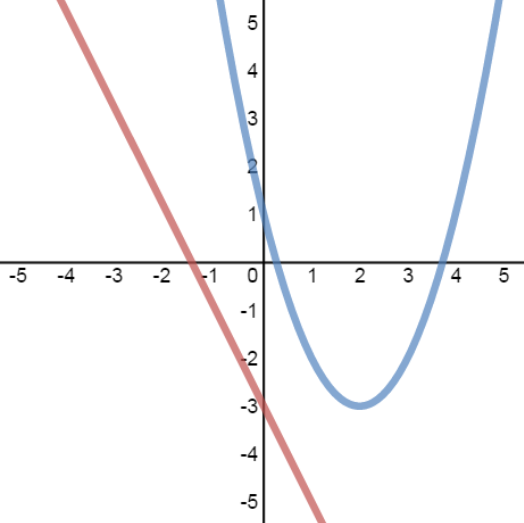
Case 1: System with 2 Solutions
Solve the system:
$y = - x + 1$
$y = x^2 + x - 2$

Step 1: Understand the Problem

We are given a system of equations consisting of one linear equation and one quadratic equation. Our goal is to find the values of $x$ and $y$ that satisfy both equations simultaneously. The equations are:
$y = -x + 1$ (Linear Equation)
$y = x^2 + x - 2$ (Quadratic Equation)

Step 2: Solving by Substitution

We will use the substitution method first. The linear equation tells us that $y$ is equal to $-x + 1$. We can substitute this expression for $y$ in the quadratic equation.
Substitute $y = -x + 1$ into $y = x^2 + x - 2$:
$-x + 1 = x^2 + x - 2$

Step 3: Simplify the Equation

To solve for $x$, we need to simplify the equation. Move all terms to one side to set the equation to zero:
$-x + 1 - x^2 - x + 2 = 0$
Combine like terms:
$0 = x^2 + 2x - 3$

Step 4: Solve the Quadratic Equation

We now have a quadratic equation $x^2 + 2x - 3 = 0$. We can solve this by factoring:
Factor the quadratic equation:
$(x + 3)(x - 1) = 0$
Set each factor to zero and solve for $x$:
$x + 3 = 0 \Rightarrow x = -3$
$x - 1 = 0 \Rightarrow x = 1$

Step 5: Find Corresponding $y$ Values

For each $x$ value, we need to find the corresponding $y$ value using the linear equation $y = -x + 1$.
For $x = -3$:
$y = -(-3) + 1 = 3 + 1 = 4$
For $x = 1$:
$y = -(1) + 1 = -1 + 1 = 0$

Step 6: Verify the Solutions

We have two solutions: $(-3, 4)$ and $(1, 0)$. To verify, we can substitute these pairs back into the original equations to ensure they satisfy both equations.
For $(-3, 4)$:
Linear equation: $4 = -(-3) + 1 = 3 + 1 = 4$ (True)
Quadratic equation: $4 = (-3)^2 + (-3) - 2 = 9 - 3 - 2 = 4$ (True)
For $(1, 0)$:
Linear equation: $0 = -(1) + 1 = -1 + 1 = 0$ (True)
Quadratic equation: $0 = (1)^2 + 1 - 2 = 1 + 1 - 2 = 0$ (True)

Step 7: Solving by Elimination

We can also solve the system using the elimination method. First, we decide which variable to eliminate. In this case, eliminating $y$ is easier.
Write the equations:
$y = -x + 1$
$y = x^2 + x - 2$
Subtract the first equation from the second to eliminate $y$:
$(x^2 + x - 2) - (-x + 1) = 0$
Simplify:
$x^2 + x - 2 + x - 1 = 0$
Combine like terms:
$x^2 + 2x - 3 = 0$
This is the same quadratic equation we solved earlier, so the solutions are the same: $x = -3$ and $x = 1$.

Step 8: Conclusion

We have successfully solved the system of linear-quadratic equations using both substitution and elimination methods. The solutions are $(-3, 4)$ and $(1, 0)$. Both methods yield the same results, confirming the accuracy of our solutions.

Here are some frequently asked questions about systems of linear-quadratic equations:

1. What is a linear-quadratic system?

A linear-quadratic system is a set of equations that combines a linear equation (first-degree) with a quadratic equation (second-degree). These systems are used to find points where a straight line intersects a parabola.

2. How many solutions can a linear-quadratic system have?

A linear-quadratic system can have three possible outcomes: two solutions (where the line intersects the parabola at two points), one solution (where the line is tangent to the parabola), or no solutions (where the line doesn't intersect the parabola).

3. What methods can be used to solve linear-quadratic systems?

Common methods for solving linear-quadratic systems include substitution (replacing a variable in one equation with its equivalent from the other equation), elimination (combining equations to cancel out a variable), and graphing (plotting both equations and finding intersection points).

4. What is the quadratic formula, and how is it used in linear-quadratic systems?

The quadratic formula, x = (-b ± (b² - 4ac)) / (2a), is used to solve quadratic equations. In linear-quadratic systems, it's often applied after substituting the linear equation into the quadratic equation to find the x-values of the solutions.

5. What are some real-world applications of linear-quadratic systems?

Linear-quadratic systems are used in various fields, including physics (for projectile motion problems), economics (for supply and demand models), engineering (for optimization problems), and computer graphics (for modeling curves and surfaces).

Understanding the system of linear-quadratic equations requires a solid foundation in several key mathematical concepts. One of the most fundamental prerequisites is graphing from slope-intercept form y=mx+b. This skill is crucial as it forms the basis for visualizing linear components within the system.

Equally important is comprehending the quadratic function in general form: y = ax^2 + bx + c. This knowledge allows students to recognize and manipulate the quadratic elements of the system. Combining these skills with word problems of graphing linear functions helps in applying theoretical concepts to real-world scenarios.

As systems often involve complex relationships, understanding graphing reciprocals of quadratic functions can provide insights into more advanced problem-solving techniques. Additionally, mastering the art of using quadratic formula to solve quadratic equations is essential for tackling the non-linear components of the system.

The nature of roots of quadratic equations: The discriminant plays a vital role in understanding the behavior of solutions within the system. This knowledge, combined with techniques for solving systems of linear equations by substitution and solving systems of linear equations by elimination, forms the core toolkit for approaching linear-quadratic systems.

Lastly, familiarity with applications of polynomial functions broadens the perspective on how these systems can be applied in various fields. This comprehensive understanding of prerequisite topics not only facilitates solving linear-quadratic systems but also enhances overall mathematical reasoning and problem-solving skills.

By mastering these prerequisite topics, students can approach the study of systems of linear-quadratic equations with confidence. Each concept builds upon the others, creating a robust framework for tackling complex problems. The interplay between linear and quadratic elements in these systems becomes clearer when one has a strong grasp of both individually. Moreover, the ability to visualize these relationships graphically, solve equations algebraically, and apply them to real-world scenarios becomes second nature with a solid foundation in these prerequisites.

In conclusion, the journey to understanding systems of linear-quadratic equations is paved with these essential prerequisite topics. Each plays a crucial role in developing the skills and intuition necessary for success in this advanced mathematical concept. By dedicating time to mastering these fundamentals, students set themselves up for a deeper, more meaningful engagement with the complexities of linear-quadratic systems.

• Solving systems of linear equations by graphing
• Solving systems of linear equations by graphing
• Solving systems of linear equations by elimination
• Solving systems of linear equations by substitution
• Solving quadratic equations by factoring
• Solving quadratic equations using the quadratic formula

• Graphing linear inequalities in two variables
• Graphing systems of linear inequalities
• Graphing quadratic inequalities in two variables
• Graphing systems of quadratic inequalities