Sign In
Sign Up
flag-us

Mastering the Slope Equation: Your Guide to Linear Functions
Unlock the power of the slope equation m = (y2-y1)/(x2-x1). Learn to calculate, interpret, and apply slopes in various scenarios. Enhance your algebra skills with our comprehensive guide.

Get the most by viewing this topic in your current grade. Pick your course now.

Now Playing:Linear function slope equation– Example 0
Intros
  1. Overview: Slopes of lines
    Overview: Slopes of lines
Examples
  1. Determine the slope using the "rise over run" method
    Slope formula: m = y_2-y_1/x_2- x_1
    1. Line A

    2. Line B

Distance formula: d=(x2−x1)2+(y2−y1)2d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
Jump to:NotesPrerequisitesRelated
Notes
In this lesson, we will try to determine slope of a straight line with different methods, for example, rise-over-run and slope formula. We only need any two of the following things: a point on a line, the slope of the line or two points on the line, we can easily find the equation of the line by using this point-slope formula. However, if you have the graph of the line and only need to find the slope, using the rise-over-run is your best way to solve the question.

What is slope?

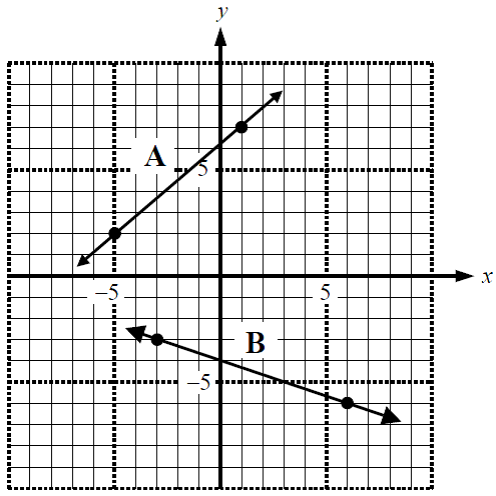
The slope of a line is essentially how angled away from the horizontal a straight line is. In a chart such as the one below, the blue line is a straight line. Making use of the graph of a line, we can find its slope.

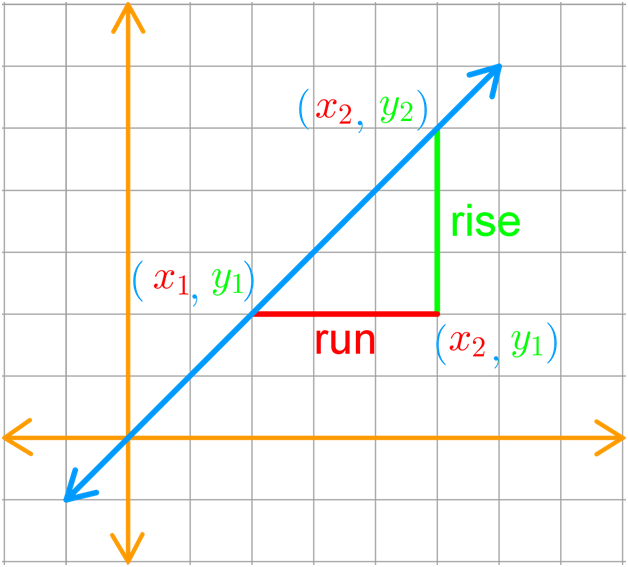
graph of a line with rise and run and coordinates on a plane
graph a line with coordinates

In order to find the slope of a line we require two points from the straight line. When you've got them, you can then put them into the slope formula to solve for the slope.

Formula for slope

The slope formula is quite simple and is as follows:

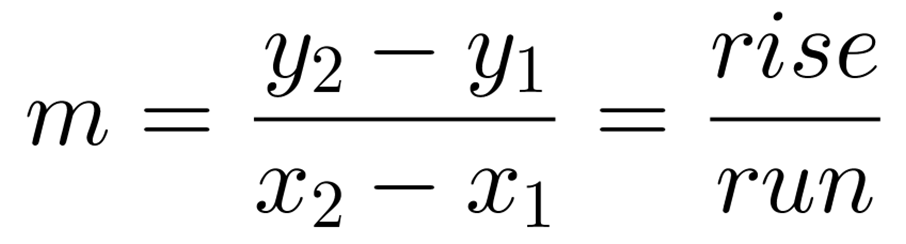
slope equation or slope formula
slope formula

A slope definition is just rise over run. m denotes the slope, whereas the subscripts of 2 and 1 in the above xx's and yy's are used to differentiate between a point number "one" and a point number "two". There is no rule that indicates which point you should designate as your first point or your second point. As long as you subtract the values in the same order, with the yy's on the top and the xx's on the bottom, you'll get the same answer.

To prove this, we can take a look at the following:

x1−x2=−x2+x1=−(x2−x1)x_1-x_2=-x_2+x_1=-(x_2-x_1)

If we take a point x1 and then subtract it by x2, it is the same as if we were to take -x2 and add it to x1. In the end, the two minus signs will cancel out, which shows that the order of the two points does not matter. The same can be done for y1 and y2. You will get the same answer for the slope no matter which point you use first and second, as long as you keep the points you designate as first and second consistent.

What does the slope mean?

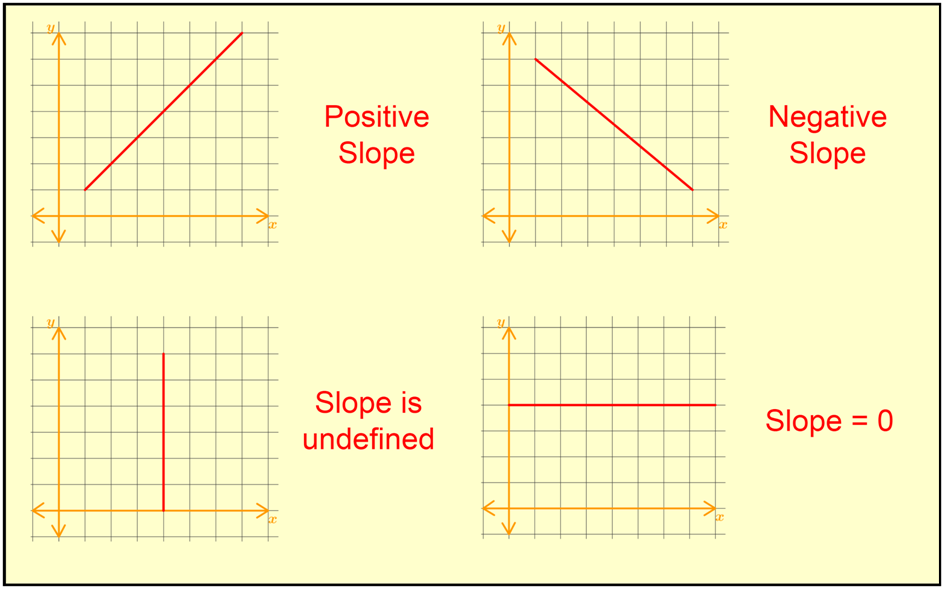
zero positive negative and undefined zero slopes
four types of slopes

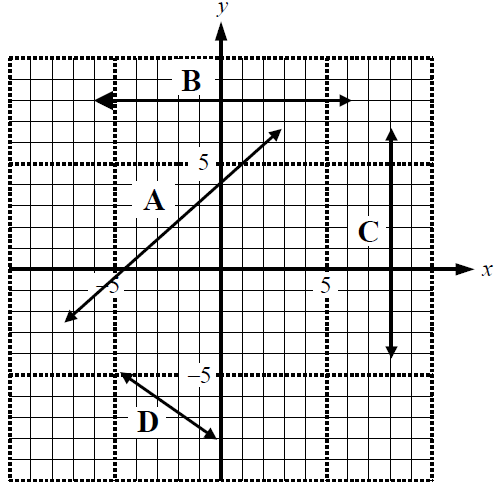
When a slope is positive, it indicates that a graph is increasing as the line progresses. If you get a negative result for a slope, it means that the line is trending downwards, and thus decreasing. This is relationship between the slope and the line that holds true at all times, so it can be useful when you need to double check your work. If you have a positive answer for a slope, look to see if the graph given is increasing. If not, you'll know that you must have made a mistake somewhere and should double check your answer.

How to find the slope of a line

What happens when a line is neither increasing nor decreasing?

For example, if the equation of the line is: y=1y = 1, the equation will look like a horizontal line that is parallel to the xx-axis. There is no run, or rise.

In this case, you'll find that the slope is not positive or negative. The slope is actually zero! To test this, try it out on two points on the y=1y=1 graph, and plug it into the slope formula.

For example,

Point 1: (1,1)(1,1)

Point 2: (−4,1)(-4,1)

m=(1−1)(−4)−(1)m = \frac{(1-1)}{(-4)-(1)}

=0−5= \frac{0}{-5}

=0= 0

The zero indicates that the graph is horizontal, and therefore the slope is neither increasing nor decreasing.

Now take the case of a vertical line. This is when a graph is, for example, x=5x=5. Would you say that the graph is increasing, or is it decreasing? In actual fact, a vertical line has no slope.

Let's look at this through an example using x=5x=5 as our line, and the slope equation.

Point 1: (5,16)(5, 16)

Point 2: (5,5)(5, 5)

m=(16−5)(5−5)m = \frac{(16-5)}{(5-5)}

=110= \frac{11}{0}

=undefined= undefined

As we cannot divide by zero, the slope cannot be found. Thus, all vertical lines have no slope and this is true for all equations of vertical lines. You'll end up dividing by zero whenever you see an equation that looks like x=x = some number, as that's the equation of a vertical line.

A point to take note of is that a vertical line and horizontal line's slope does not mean the same thing. Having a slope of zero does not equal having no slope. Instead, horizontal lines do have a slope, and that is why when you calculate their slope with the slope equation, you'll get a number: zero.

If you're stuck on a problem or want to double check your work, feel free to reference this online slope calculator that makes use of the slope equation.