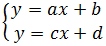Depending on whether and how the linear equations in a system touch each other, there will be different number of solutions to the system. There can be one solution, no solution and even infinite solution.
Mastering the Art of Determining Solutions in Linear Equations Unlock the power of linear equations! Learn to confidently determine the number of solutions in various scenarios, from single equations to complex systems. Enhance your problem-solving skills today.
Intros
Examples
Free to Join!
StudyPug is a learning help platform covering math and science from grade 4 all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction
Welcome to our exploration of determining the number of solutions to linear equations! This fundamental concept in algebra is crucial for understanding more complex mathematical ideas. Our introduction video serves as an excellent starting point, providing a clear and concise overview of the topic. As we delve into this subject, we'll discover that linear equations can have one solution, no solution, or infinitely many solutions. This knowledge is particularly valuable when working with systems of equations, where multiple linear equations are considered simultaneously. By mastering this concept, you'll be better equipped to tackle more advanced mathematical problems and real-world applications. Remember, understanding the number of solutions is key to interpreting the relationships between variables in various scenarios. So, let's embark on this mathematical journey together, unraveling the mysteries of linear equations and their solutions!
Here are some frequently asked questions about determining the number of solutions to linear equations:
1. How do you determine how many solutions a system of equations has?
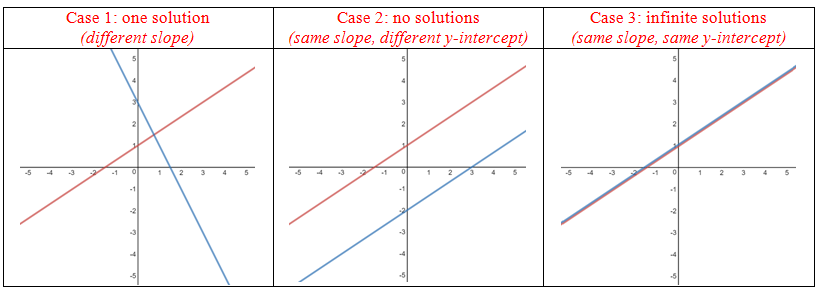
To determine the number of solutions in a system of equations, compare the slopes and y-intercepts of the equations: - If the slopes are different, there is one solution (lines intersect). - If the slopes are the same but y-intercepts differ, there are no solutions (parallel lines). - If both slopes and y-intercepts are identical, there are infinite solutions (same line).
2. How do you know if an equation has many solutions?
An equation has many (infinite) solutions when it represents an identity, meaning the left side is equivalent to the right side for all values of the variable. For example, in the equation 2x + 4 = 2(x + 2), both sides simplify to the same expression, indicating infinite solutions.
3. How do you decide whether a number is a solution of the equation?
To check if a number is a solution, substitute it into the equation for the variable. If the resulting statement is true (left side equals right side), the number is a solution. For example, in 2x + 3 = 7, x = 2 is a solution because 2(2) + 3 = 7 is true.
4. How can you determine the number of real number solutions of a system of equations?
Graph the equations and observe their relationship: - One intersection point: One solution - No intersection: No solution - Lines overlap completely: Infinite solutions Alternatively, solve the system algebraically and interpret the result (unique solution, contradiction, or identity).
5. How do you find the number of solutions in a quadratic equation?
For a quadratic equation ax² + bx + c = 0: - Calculate the discriminant: b² - 4ac - If discriminant > 0: Two real solutions - If discriminant = 0: One real solution (double root) - If discriminant < 0: No real solutions (two complex solutions) The number of solutions corresponds to the number of x-intercepts in the parabola's graph.
Understanding the number of solutions to linear equations is a crucial skill in algebra, but it requires a solid foundation in several prerequisite topics. One of the most fundamental skills is solving linear equations by substitution. This method is essential because it allows you to manipulate equations and find points of intersection, which directly relates to the number of solutions.
Another critical concept is graphing from slope-intercept form y=mx+b. Understanding the slope of the line and how it affects the graph is crucial when visualizing the potential intersections of linear equations. This visual representation helps in determining whether equations have one, infinite, or no solutions.
Building on this, graphing linear functions using a single point and slope is equally important. This skill allows you to quickly plot lines and understand their relationships, which is key to identifying the number of solutions in a system of equations.
The concept of parallel and perpendicular lines in linear functions is particularly relevant. Parallel lines, for instance, never intersect, indicating no solutions, while perpendicular lines always intersect at exactly one point, guaranteeing a single solution.
Understanding special cases like vertical lines and horizontal lines of linear equations is crucial. These cases often lead to unique solution scenarios and are essential in comprehending the full spectrum of possible outcomes when determining the number of solutions.
Familiarity with the coordinate plane, as studied in topics like conics, provides the spatial understanding necessary to visualize intersections and solutions. This geometric perspective complements the algebraic approach to solving linear equations.
Lastly, practical applications such as distance and time questions in linear equations demonstrate the real-world relevance of these concepts. They show how determining the number of solutions can have practical implications in problem-solving scenarios.
By mastering these prerequisite topics, students gain a comprehensive understanding of the factors that influence the number of solutions in linear equations. This foundational knowledge not only aids in solving specific problems but also develops critical thinking skills essential for advanced mathematical concepts.