The solutions to a system of equations are the points of intersection of the lines. For a system with two quadratic equations, there are 4 cases to consider: 2 solutions, 1 solution, no solutions, and infinite solutions.
Systems of Quadratic Equations: Mastering Advanced Algebra Unlock the power of quadratic systems! Learn essential techniques to solve complex equations, visualize solutions, and apply your skills to real-world problems. Elevate your algebra prowess today.
Intros
- • The solutions to a system of equations are the points of intersection of the graphs.
• For a system consisting of two quadratic equations:
quadratic equation: y=ax2+bx+c
quadratic equation: y=dx2+ex+f
There are 4 cases to consider:case 1: 2 solutions case 2: 1 solution case 3: no solutions case 4: infinite solutions
Examples
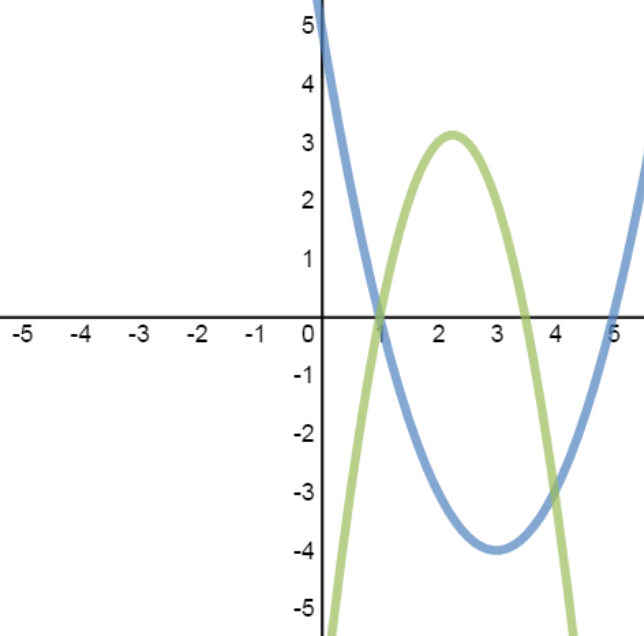
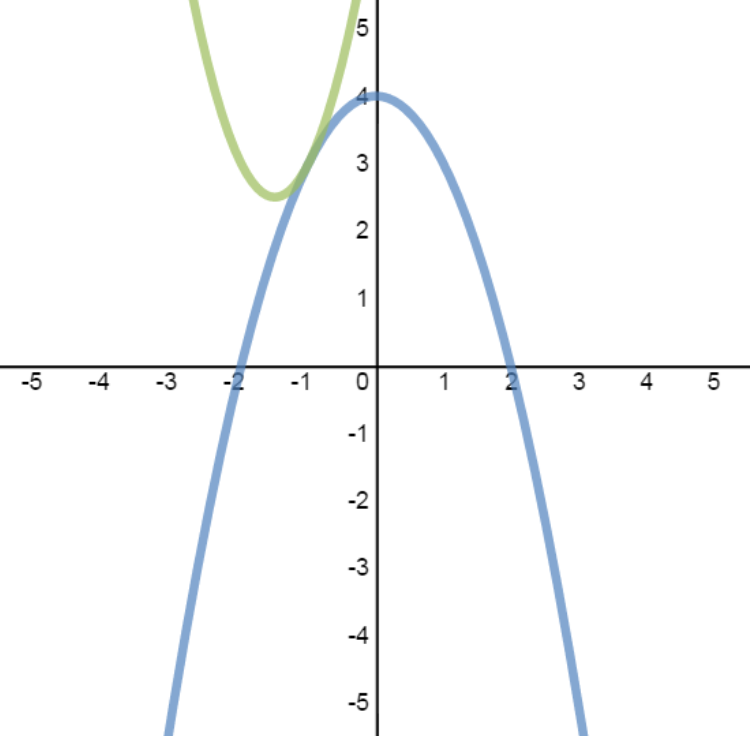
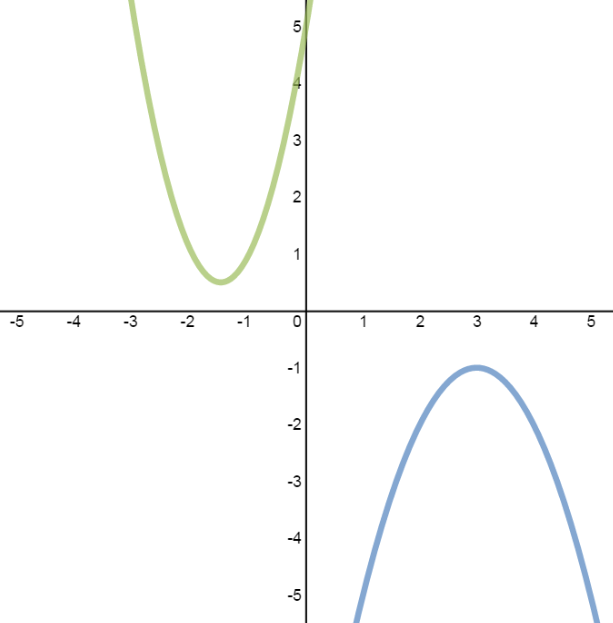
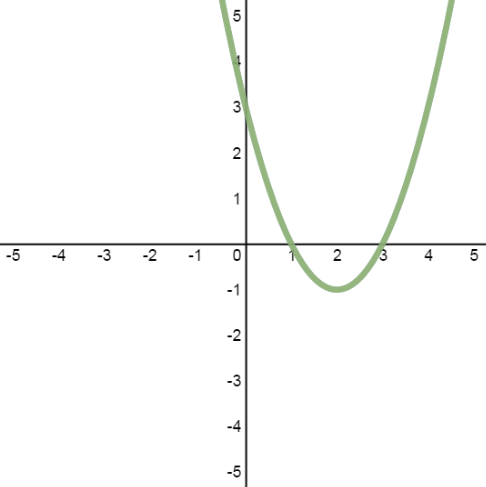
- Case 1: System with 2 Solutions
Solve the system, then verify the solutions graphically:
y=x2−6x+5
y=−2x2+9x−7
- Case 2: System with 1 Solution
Solve the system, then verify the solutions graphically:
y=2x2+6x+7
y=−x2+4
- Case 3: System with No Solutions
Solve the system, then verify the solutions graphically:
y=−x2+6x−10
y=2x2+6x+5
- Case 4: System with Infinite Solutions
Solve the system, then verify the solutions graphically:
x2−4x−y+3=0
5y−5x2+20x−15=0
Free to Join!
StudyPug is a learning help platform covering math and science from grade 4 all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction to Systems of Quadratic-Quadratic Equations
A system of quadratic-quadratic equations is a mathematical concept that involves solving two or more quadratic equations simultaneously. This topic is crucial in advanced algebra and has numerous real-world applications. The introduction video provides a comprehensive overview of this system, offering visual representations and step-by-step explanations that significantly enhance understanding. It's important to note that the solutions to a system of quadratic equations are the points where the curves representing these equations intersect. These intersection points can be found graphically or through algebraic methods. The quadratic system can have up to four solutions, depending on how the curves intersect. Mastering this concept opens doors to solving complex problems in physics, engineering, and quadratic equations in economics. As we delve deeper into this topic, we'll explore various methods for solving these systems and analyze their practical applications in different fields.
Understanding the solutions to quadratic systems is essential for tackling more advanced problems. By mastering the techniques for finding these solutions, students can apply their knowledge to a variety of disciplines, including physics and engineering. Additionally, the ability to solve quadratic equations in economics can provide valuable insights into market behaviors and financial trends.
Q1: How do you solve the system of quadratic equations?
A1: To solve a system of quadratic equations, you can use several methods: 1. Substitution: Isolate one variable in one equation and substitute it into the other. 2. Elimination: Multiply equations to align coefficients and add/subtract to eliminate a variable. 3. Graphical method: Plot both equations and find intersection points. 4. Using technology: Employ graphing calculators or computer algebra systems. Choose the method based on the specific equations and your comfort level with each technique.
Q2: What are the 4 methods for solving quadratic equations?
A2: The four main methods for solving quadratic equations are: 1. Factoring: Break down the equation into factors and set each to zero. 2. Quadratic formula: Use the formula x = (-b ± (b² - 4ac)) / (2a) for ax² + bx + c = 0. 3. Completing the square: Rewrite the equation to create a perfect square trinomial. 4. Graphing: Plot the quadratic function and find x-intercepts.
Q3: What are 4 examples of quadratic equations?
A3: Here are four examples of quadratic equations: 1. x² + 5x + 6 = 0 2. 2x² - 7x - 15 = 0 3. x² - 9 = 0 4. 3x² + 2x - 1 = 0 These equations can be solved using various methods like factoring, the quadratic formula, or completing the square.
Q4: What is a quadratic system?
A4: A quadratic system is a set of two or more equations where at least one equation is quadratic (contains a variable raised to the second power). For example: { x² + y = 7 x + y² = 5 } Solving such systems involves finding ordered pairs (x, y) that satisfy all equations simultaneously.
Q5: How do you solve quadratic equations step by step?
A5: To solve a quadratic equation step by step: 1. Arrange the equation in standard form: ax² + bx + c = 0 2. Try factoring if possible 3. If not factorable, use the quadratic formula: x = (-b ± (b² - 4ac)) / (2a) 4. Simplify the expression under the square root 5. Calculate the two solutions (if real) 6. Check your answers by substituting them back into the original equation
Understanding the system of quadratic-quadratic equations requires a solid foundation in several key mathematical concepts. To master this advanced topic, students must first grasp the fundamentals of solving quadratic equations using various methods, including the quadratic formula. This skill is crucial as it forms the basis for tackling more complex systems involving multiple quadratic equations.
Another essential prerequisite is graphing quadratic inequalities in two variables. This knowledge helps students visualize the solutions of quadratic-quadratic systems and understand their geometric representations. Familiarity with the coordinate plane and conic sections, particularly circles, is also beneficial when dealing with these systems.
The nature of roots of quadratic equations, including the concept of the discriminant, plays a vital role in analyzing the solutions of quadratic-quadratic systems. This knowledge helps students predict the number and types of solutions they might encounter.
Understanding quadratic functions in vertex form is another crucial prerequisite. This form allows students to easily identify key features of quadratic equations, which can be invaluable when solving and interpreting systems of quadratic-quadratic equations.
While quadratic equations are the focus, proficiency in solving systems of linear equations by substitution and elimination provides a strong foundation for tackling more complex systems. These techniques often come into play when simplifying or manipulating quadratic-quadratic systems.
Additionally, graphing systems of quadratic inequalities is a closely related skill that enhances students' ability to visualize and interpret the solutions of quadratic-quadratic systems. This knowledge is particularly useful when dealing with constraints or regions defined by multiple quadratic equations.
Lastly, proficiency in solving quadratic inequalities is essential. This skill allows students to understand and interpret the solution sets of quadratic-quadratic systems, especially when dealing with inequalities or constraints within these systems.
By mastering these prerequisite topics, students will be well-equipped to tackle the challenges presented by systems of quadratic-quadratic equations. Each concept builds upon the others, creating a comprehensive understanding of the relationships between quadratic functions and their applications in more complex mathematical scenarios. This solid foundation not only facilitates learning but also enhances problem-solving skills and mathematical intuition, essential for success in advanced algebra and beyond.