Theoretical vs. Experimental probability
0/4
Intros
Lessons
- Theoretical probability and expected outcomes
- Finding experimental probability and comparing with experimental probability
- Giving experimental probability as a fraction
- Review on theoretical probability vs. experimental probability
0/9
Examples
Lessons
- Theoretical probability and expectations
- How many times would you expect to land on heads if you flipped a coin 10 times?
- How many times would you expect to roll the number 2 if you toss a six-sided die 30 times?
- How many times would you expect to land on the letter A if you spin a four-part spinner 40 times?
- The experiment will consist of pulling 1 lollipop out of the bag at a time. Each lollipop is put back into the bag before the next pull.
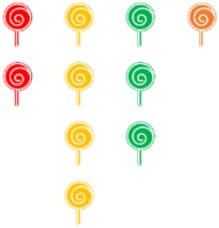
- How many times would you expect to pull a red lollipop if you tried 20 times?
- How many times would you expect to pull a red lollipop if you tried 20 times?
- How many times would you expect to land on a number greater than 4 if you toss a six-sided die 9 times?
- Comparing experimental probability and theoretical probability (results in reality vs. expectation)
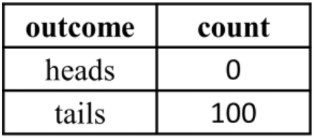
A student is preparing to conduct a probability experiment flipping a coin. They will record their results in a table: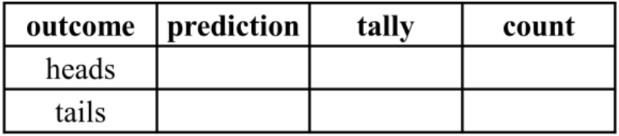
- What (theoretical) probability fraction is expected for each outcome?
- Which of the following seems most likely to happen if the coin will be flipped 100 times?
- 75 heads, 25 tails
- 0 heads, 100 tails
- 55 heads, 45 tails
- Write the experiment probability for P(heads) and P(tails) in the student's experiment with the completed results. Do the results match the expected probabilities? Explain.

- In this scenario, every time the coin was flipped, it landed on tails facing up. Normally this would be extremely rare (near impossible). What are some explanations for what happened?