Sign In
Sign Up
flag-sg

Theoretical vs. Experimental probability

Topic Notes

In this lesson, we will learn:

  • The difference between theoretical and experimental probability
  • How to calculate the number of expected outcomes using theoretical probability and number of experimental trials
  • How to write the experimental probability as a fraction based off the observed results in an experiment

Notes:

  • Probability for simple events means we are just looking at one probability scenario at a time (i.e. one coin flip; a single six-sided die toss; one spinner)

  • There are two types of probability:
    • Theoretical probability is an educated guess on what you think should or will happen ("expected" probability; based on theory)
    • Experimental probability is based on an experiment and what you saw happen already ("observed" probability; happened in reality)

  • The probability we have seen so far in previous lessons is based on theoretical probability. We can use theoretical probability to find the number of expected outcomes.
    • Before you do an experiment, you can predict how many times an outcome will happen (how many times it should theoretically happen)

      PP (event) = number outcomes wantedtotal number possible outcomes\frac{number\,outcomes\,wanted} {total\,number\,possible\,outcomes}

    • This is based on the number of trials you will do in the experiment. A trial is each run through of the experiment--1 trial will give 1 outcome (each coin flip, each dice toss, each spinner spin)

      # expected outcomes = PP (event) × # trials

  • The experimental probability is based off the observations made during the experiment and calculated once all trials are completed.

    PP (experimental event) = number outcomes observedtotal number trials\frac{number\,outcomes\,observed} {total\,number\,trials}

Ex. For an experiment, a coin is flipped 8 times. The results are shown in an observation table:
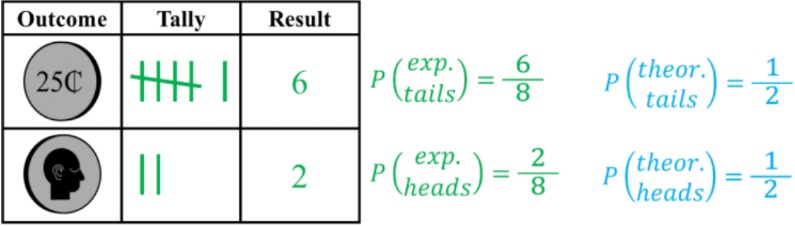
Theoretical vs. experimental probability
    • The experimental (exp.) probabilities do not match with the theoretical (theor.) probabilities.
    • The more trials you do, the closer the results should get to the expected probabilities (i.e. doing 10 trials vs. 100 trials vs. 1000 trials, etc.)