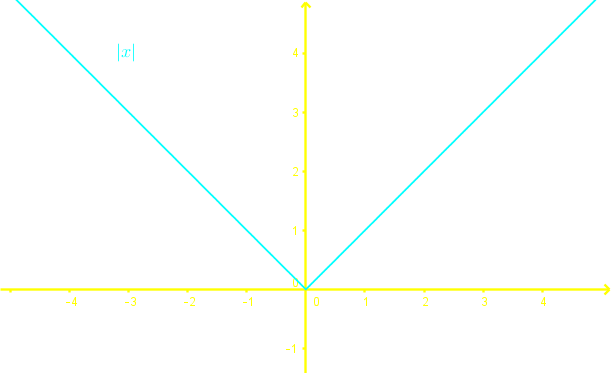
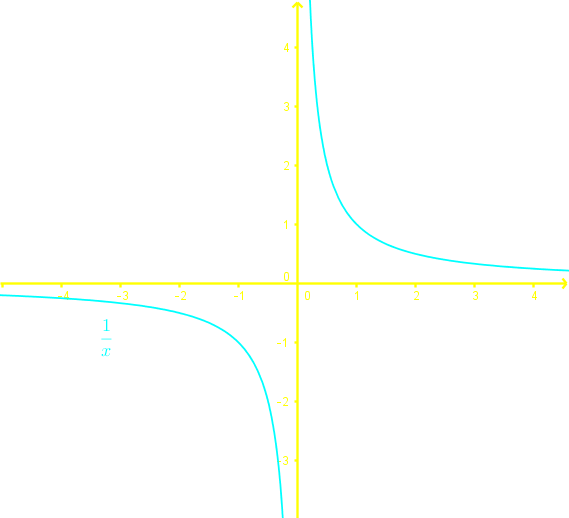
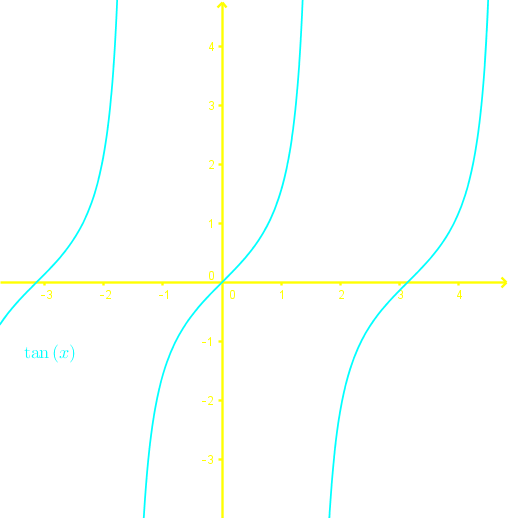
To determine if an expression is a function, we perform the vertical line test.
Surjective/Onto: For every value, there exists at least one value.
Injective/Into/one-to-one: For every value, there exists at most one value.
To determine if a function is one-to-one, we perform the horizontal line test.