Solving first degree trigonometric equations

Solving First Degree Trigonometric Equations

Trigonometric Equations:

Put simply, trigonometric equations are just equations that feature the trigonometric ratios such as sine and cosine on the variable "$x$". Because of the presence of these trigonometric functions, solving these equations becomes a little more difficult. But, before we get into solving these trig equations, let's make sure we understand what $1^{st}$ degree trig equations are! Below are a couple of examples of trig equations:

There are also other levels of trig equations, including $2^{nd}$ degree trig equations. Below are a couple examples of $2^{nd}$ degree trig equations:

Notice how the above equations feature our familiar polynomial format but with the addition of the trigonometric ratios sine and cosine. Now that we have an idea of what trig equations look like, let's look at how to solve first degree trig equations!

Unit Circle Table:

Oftentimes when we are dealing with first degree trig equations, we will be using the special right angles, reference angles, and the unit circle to solve for the variable $x$ (or whatever the variable is). Below is a copy of the unit circle chart, which gives the unit circle degrees and radians.

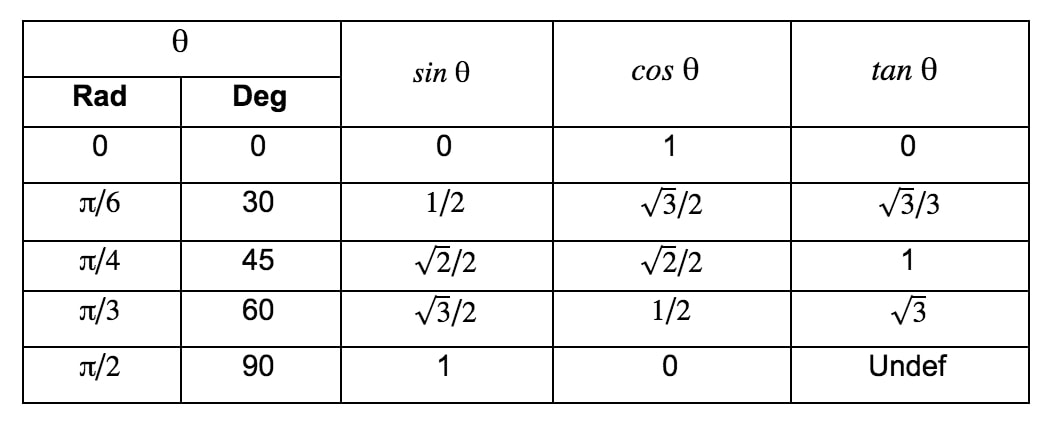
NOTE: This chart just gives the values for sine, cosine, and tangent in the first quadrant using the common reference angle. The values are based on some special triangles you should be familiar with, including the 45 45 90 triangle and the 30 60 90 triangle.

If you recall, these values will vary in their sign (+ / -) depending on which quadrant the angle is in. We can use the acronym ASTC (All Students Take Calculus) to help us to remember which trig ratio is what in each quadrant:

Lastly, it is important to recall our handy acronym SOHCAHTOA to find missing angles. Below are the formulas we get from SOHCAHTOA, as well as an image to help you visualize it:

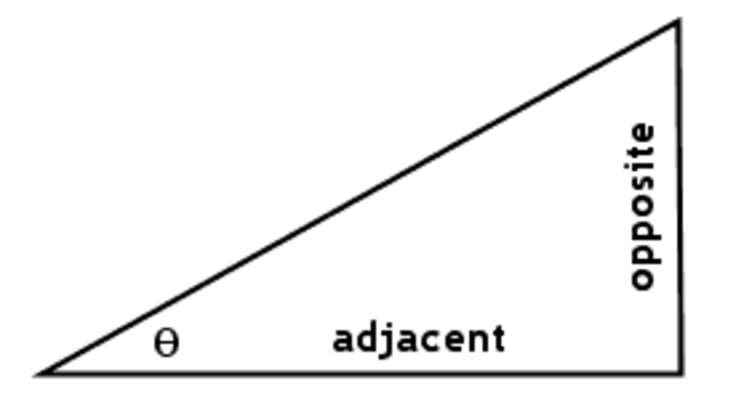
For a review of some of these concepts in a more detailed video, check out our clips on the reference angle, the exact values of trig functions, and All Students Take Calculus. Also, see our videos on special right triangles 45 45 90 and special right triangle 30 60 90.

As always, the best way to practice is to do some examples!

Example 1:

For the following trigonometric equation, find the exact value for $x$ for each of the following conditions:

i) For 0° $\leq x \leq$ 360°

ii) General solution in degree measure

iii) For 0° $\leq x \leq 2\pi$

iv) General solution in radian measure

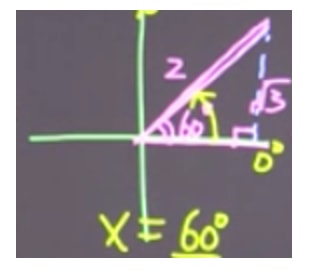
Step 1: Identify if a Special Angle/Triangle is Present

The presence of such angles or triangles makes find the solution much easier, as you should have these angles memorized! Notice that $\frac{\sqrt{3}}{2}$ is a special triangle:

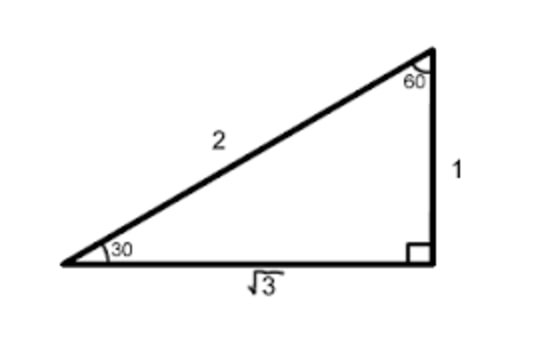
Therefore, since sine by definition is $\frac{opposite}{hypotenuse}$, the reference angle for $\frac{\sqrt{3}}{2}$ is 60°.

Step 2: Use ASTC to Identify Where This Angle Exists

For sine to be positive, the angles must be in first and second quadrants.

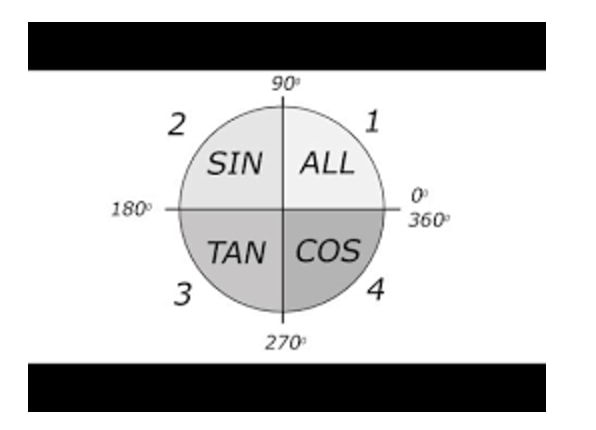
Thus, in the first quadrant, the angle is 60°. In the second quadrant, the angle is 180°- 60° = 120°

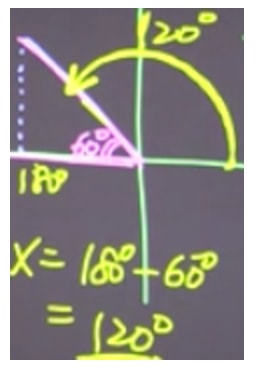
Step 3: Solve the Remainder of the Question

ii) 60° + 360°$n$, where $n$ is a whole integer; 120° + 360°$n$, where $n$ is a whole integer.

iii) $x = \frac{\pi}{3},\;x = \frac{2\pi}{3}$

* just convert answer i) from degrees to radians

iv) $\frac{\pi}{3} + 2\pi n$ where $n$ is a whole integer; $\frac{2\pi}{3} + 2\pi n$, where $n$ is a whole integer.

* just convert answer iii) from degrees to radians

Example 2:

For the following trigonometric equation, find the exact value for $x$:

In this case, since we know that $-0.4$ is not a special case, we must use a calculator to find $x$. NOTE: when solving via a calculator, first remove the sign. We can identify the quadrant using ASTC later on.

Then use reference angle and quadrants to find solutions. According to ASTC, cosine is negative in the second and third quadrants. Therefore:

And that's all there is to it! For an excellent tool to check you work, check out this useful calculator tool here. And, for further study, see our video on the derivative of trigonometric functions.

• Reference angle
• Find the exact value of trigonometric ratios
• ASTC rule in trigonometry (All Students Take Calculus)

• Solving expressions using 45-45-90 special right triangles
• Solving expressions using 30-60-90 special right triangles
• Derivative of trigonometric functions