What is a 30-60-90 triangle?
One of the two special right triangles you'll be facing in trigonometry is the 30-60-90 triangle. The other one is the 45 45 90 triangle. These triangles are special triangles because the ratio of their sides are known to us so we can make use of this information to help us in right triangle trigonometry problems.
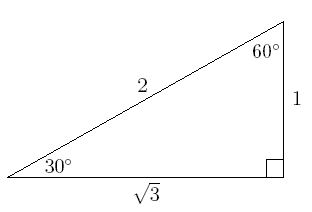
In the case of the 30-60-90 triangle, their side's ratios are 1 : 2 : . We'll prove that this is true first so that you can more easily remember the triangle's properties.
A 30-60-90 triangle is actually half of an equilateral triangle.
Triangle ABC shown here is an equilateral triangle. Since it's equilateral, each of its 3 angles are 60 degrees respectively. Its sides are also equal.
If we draw a line AD down the middle to bisect angle A into two 30 degree angles, you can now see that the two new triangles inside our original triangle are 30-60-90 triangles.
We know that BD is equalled to DC, which is also equalled to half of AB since AB was originally equalled to BC before it was split in half. So therefore, the ratio of BD : AB is 1 : 2.
Since we have a hypotenuse due to the 90 degree angle that exists inside our triangle, we can use the pythagorean theorem to figure out the last side: AD.
And there you have it! You now know how all the sides of the 30-60-90 triangles came about. Let's move on to solving right triangles with our knowledge on the sides' ratios.
Solve for 30 60 90 triangle
Here we have a 30-60-90 special right triangle, with the three interior angles of 30, 60, 90 degrees. We know that the length of each side in this triangle is in a fixed ratio. We can now use the ratio to solve the following problem.
Question 1:
If Θ = 30° , find the exact value of the following expression:
sin 2Θ
Solution:
Since Θ = 30°, sin 2Θ = sin 60°.
We know that sin Θ =
Since we are looking for the value of sin 60°, we are going to look at the 60° angle in the special triangle and find out the opposite side and hypotenuse of the angle. And we found that the opposite side = 3 and the hypotenuse = 2. Then, we put the numbers into sin 60° = . This gives us the final answer of
Question 2:
If Θ=60° , find the exact value of the following expression:
Solution:
First, we put Θ = 60° into . We get
4 = (30°)
From the special triangle, we know that sin 30° =
Then, we can now solve the cubic root:
=
The final answer is
A good online resource to help you check your work when it comes to 30-60-90 triangles (or even 45 45 90 triangles!) can be found here. You can also play along with this online scalable 30-60-90 triangle to see how the sides change while staying in the 1 : 2 : ratio.