Surface area of 3-dimensional shapes

Surface area of 3D shapes

Prior to this, you've probably learned how to find the surface area of 2D shapes—for example, the area of a square or a rectangle. But how about 3D shapes? You can find the surface area for them too! Finding the area of 3D shapes just means finding the sum of all the areas of the outside surfaces on a shape.

What is a prism?

In geometry, a prism is a polyhedron. This means that is has two faces that are the same called the bases of the prism. Other faces of the prism are all parallelograms. Oftentimes, when you're finding the surface area of a 3D shape, you'll be working with a prism such as a 3D triangle.

What is a rectangular prism

Amongst the prisms, the most popular one people usually start with are rectangular prisms. A rectangular prism has rectangles as its two bases. It's a 3D rectangle. To find the surface area of it, you simply find the areas of the six rectangles that make up its shape.

Example problems

We'll guide you through a few questions dealing with the surface area of a prism. As we mentioned before, most starter problems take you through questions that deal with a rectangular prism first, and that's what we'll be doing here.

Question 1

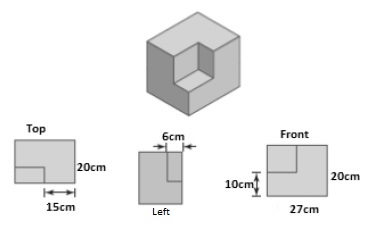
a) What are the dimensions of the cutout piece?

Solution:

From the question's diagrams, we can determine the measurements of the cutout piece. You can find the below numbers by finding the side of the rectangle and then subtracting the parts that aren't part of the cutout piece. For example, the length of one of the rectangle's side is 27cm. The side right beside the cutout piece is 15cm. Subtracting 15 from 27 gives us 12, and therefore, the cutout piece has a length of 12.

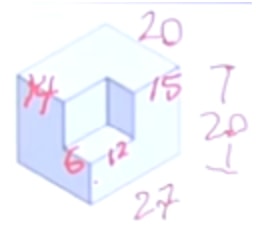
Here are the measurements for the cutout piece if we isolated it.

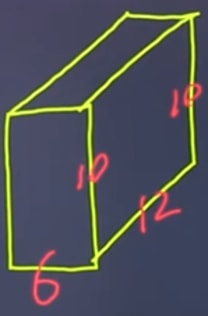
b) How does the surface area of the original rectangular object change after cutting out the corner piece?

Solution:

Surface area is not equalled to the volume. If you were to look at this shape from top, left, or right, you'll still see the whole rectangle. The surface area actually didn't change.

Therefore, there is no change.

Question 2:

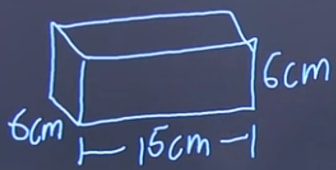
Below is a rectangular object formed by six blocks which all have the same size.

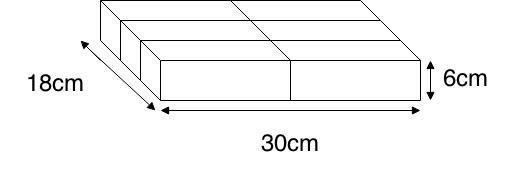
a) What are the dimensions of one block?

Solution:

Since the six blocks are equal, the dimensions of one block can be found by dividing up the measurements into appropriate amounts to allocate its portion to the respective block. The 6cm actually remains the same since the height of 1 block versus the whole rectangular object is the same.

The 30cm has to be divided into 2, giving us 15 cm. The 18cm will have to be divided into 3 sections, which is 6cm each. Therefore our final dimensions is:

b) What is the surface area of the rectangular object?

Solution:

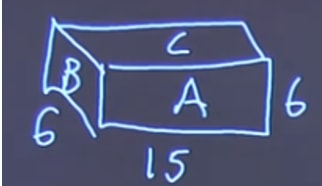
Side A: (15 $\times$ 6) $\times$ 2 = 180

Side B: (6 $\times$ 6) $\times$ 2 = 72

Side C: (15 $\times$ 6) $\times$ 2 = 180

180 + 72 + 180 = 432 $cm^{2}$

c) Calculate the ratio of the surface area of the rectangular object to the total surface area of the six blocks.

Solution:

We have the surface area of one block. We now need to look the surface area of the whole object.

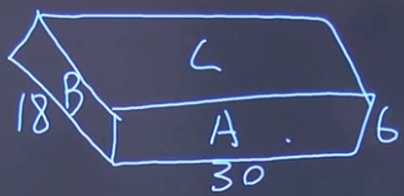
Side A: (30 $\times$ 6) $\times$ 2 = 360

Side B: (18 $\times$ 6) $\times$ 2 = 216

Side C: (30 $\times$ 18) $\times$ 2 = 1080

360 + 216 + 1080 = 1656 $cm^{2}$

Then the ratio is equalled to: $\frac{432}{1656}$, which when simplified equals $\frac{6}{23}$.

Feel free to play around with this interactive geometry shape that can show you how the surface area of 3D objects are calculated.

To further your understanding of the surface area of a 3D object, take a look at the surface area and volume of prisms lesson, or the ones on pyramids, cylinders, cones, or spheres.