Sign In
Sign Up
flag-us

Trigonometric ratios of angles in radians

Get the most by viewing this topic in your current grade. Pick your course now.

Now Playing:Trigonometric ratios of angles in radians – Example 1a
Examples
  1. Find the value
    1. sin π3 {\pi \over 3}

    2. cos 3π4 {{3 \pi} \over 4}

    3. tan 7π6 {{7 \pi} \over 6}

    4. sin 11π6 {{11 \pi} \over 6}

    5. sec −8π3 -{{8 \pi} \over3}

    6. sec −8π3 -{{8 \pi} \over3} shortcut

Angle in standard position
Jump to:NotesPrerequisitesRelated
Notes

Common Trigonometric Ratios

What are Trigonometric Ratios?

In the world of calculus, pre-calculus, and trigonometry, trigonometric ratios are a powerful and commonly used tool. With proper understanding, they are very easy to use as well!

In order to understand trigonometric ratios, let's first look back on some basic trigonometry principles. First, the Pythagorean Theorem with right triangles, and SOHCAHTOA. If you recall, we can use the Pythagorean Theorem (a2+b2=c2)(a^{2} + b^{2} = c^{2}) to solve for unknown side lengths of right triangles, and we can use SOHCAHTOA to find missing angles. Below are the formulas we get from SOHCAHTOA, as well as an image to help you visualize it:

sin⁡x=oppositehypotenuse,cos⁡x=adjacenthypotenuse,tan⁡x=oppositeadjacent\sin x = \frac{opposite}{hypotenuse}, \cos x = \frac{adjacent}{hypotenuse}, \tan x = \frac{opposite}{adjacent}

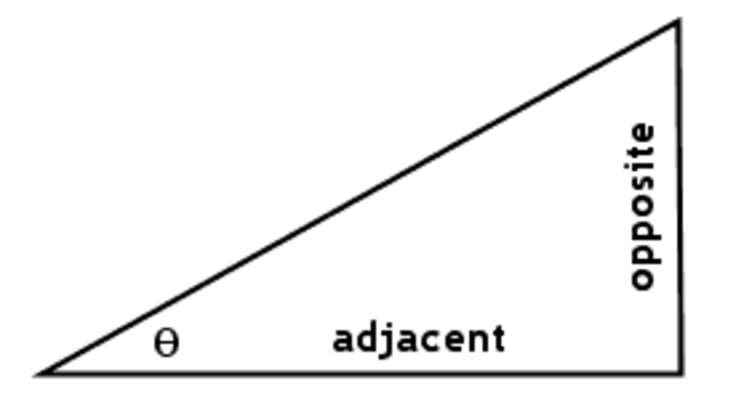
To visualize adjacent, opposite and hypotenuse
To visualize the sides of a triangle

Using all of this information, as we further our study into pre-calculus and trigonometry, we will encounter what are known as "trigonometric ratios" – that is, simply just using SOHCAHTOA for important and commonly encountered angles.

Common Trigonometric Ratios:

Now, let's use the above recalled information to look at what trigonometric ratios are in concrete terms. Below is a table that summarizes the most important trigonometric ratios for sin⁡x,cos⁡x,tan⁡x,csc⁡x,sec⁡x\sin x, \cos x, \tan x, \csc x, \sec x, and cot⁡x\cot x.

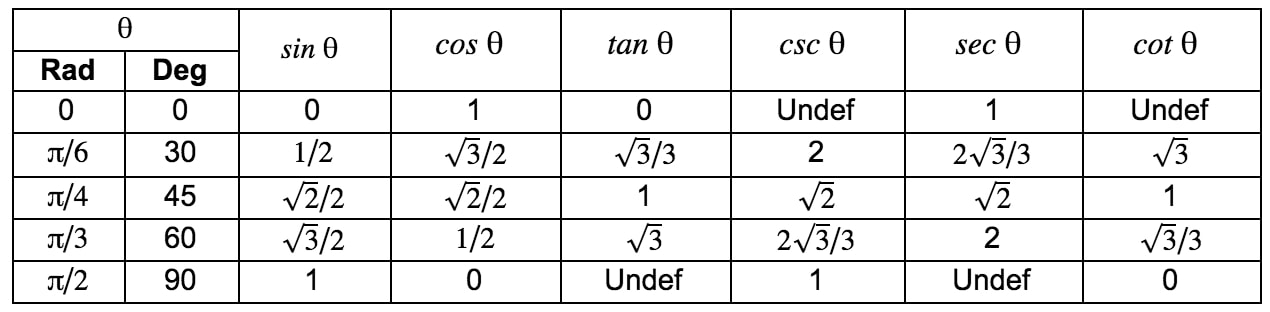
Chart of common trigonometric ratios
Common trigonometric ratios

This above trig chart gives all the unit circle values for the first quadrant. As you can see, angles are listed in degrees and in radians. You should know both, but you're most likely to be solving problems in radians. Now, the next natural question is, how can I remember these trigonometric ratios? The answer – memorization, and a few helpful little tricks.

How to Find Trigonometric Ratios:

Memorizing the common trigonometric ratios in the table above is actually much easier than you would think. Though we can't completely forego memorization, we can make our lives a little easier using this one, incredibly useful trick.

Trick:

Because of the following 4 equations, we only need to memorize the unit circle values for sine and cosine.

tan⁡θ=sin⁡θcos⁡θ,cot⁡θ=cos⁡θsin⁡θ,sec⁡θ=1cosθ,csc⁡θ=1sin⁡θ\tan \theta = \frac{\sin \theta}{\cos \theta}, \cot \theta = \frac{\cos \theta}{\sin \theta}, \sec \theta = \frac{1}{ cos \theta}, \csc \theta = \frac{1}{\sin \theta}

With these 4 equations, we don't even need to memorize the trig ratios with tan, cot, sec, or csc! Of course, this recommendation will make questions take longer to solve. So, if you're aiming for speed, try memorizing the whole trig chart above!

Now that we have an idea of how to handle trig ratios, the best way to get comfortable with them is to solve some trigonometry problems.

Solving Trigonometric Equations:

Example 1:

Find cos⁡0+sin⁡π2+sec⁡0\cos 0 + \sin \frac{\pi}{2} + \sec 0

Step 1: Evaluate Trigs Individually

First, let's focus on radians. Let's assume we have only memorized the trigonometric ratios for sin and cos. With this assumption, we know we can easily evaluate the first two trig ratios cos⁡0\cos 0 and sin⁡π2\sin \frac{\pi}{2}. The third ratio, sec⁡0\sec 0, however, requires an extra step using the trick we discussed earlier.

= 1+1+1cos⁡01 + 1 + \frac{1}{\cos 0}

= 1+1+111 + 1 + \frac{1}{1}

= 1+1+11 + 1 + 1

Step 2: Solve

Now that we've evaluated all of the trig ratios, all we have to do is solve the simple expression above.

= 33

Example 2:

Find sin⁡90+cos⁡90−tan⁡60\sin 90 + \cos 90 - \tan 60

Step 1: Evaluate Trigs Individually

Now let's focus on degrees. Again, let's assume we have only memorized the trigonometric ratios for sin and cos. With this assumption, we know we can again easily evaluate the first two trig ratios easily. The third ratio, however, requires the same trick we used in the previous question, but in this case on tan⁡60\tan 60 degrees.

= 1+0−sin⁡60cos⁡601 + 0 - \frac{\sin 60}{\cos 60}

= 1+0−32121 + 0 - \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}

= 1+0−31 + 0 - \sqrt{3}

Step 2: Solve

Now that we've evaluated all of the trig ratios, all we have to do is solve the simple expression above. Though we try to avoid the use of calculators when using trig ratios, we can certainly use one in this case.

=0.732= 0.732

Example 3:

Find tan⁡π3+tan⁡π2+sec⁡π4\tan \frac{\pi}{3} + \tan \frac{\pi}{2} + \sec \frac{\pi}{4}

Step 1: Evaluate Trigs Individually

For the last example, let's try something a bit more challenging. Again, let's assume we have only memorized the trigonometric ratios for sin and cos. With this assumption, we are still unable to find any of the trig ratios without using our trick, so we have to a bit more work.

sin⁡π3cos⁡π3+sin⁡π2cos⁡π2+1cos⁡π4\frac{\sin \frac{\pi}{3}}{\cos \frac{\pi}{3}} + \frac{\sin \frac{\pi}{2}}{\cos \frac{\pi}{2}} + \frac{1}{\cos \frac{\pi}{4}}

3212+10+122\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} + \frac{1}{0} + \frac{1}{\frac{\sqrt{2}}{2}}

3+10+22\sqrt{3} + \frac{1}{0} + \frac{2}{\sqrt{2}}

Step 2: Solve

Now that we've evaluated all of the trig ratios, all we have to do is solve the expression above. However, in this case, it is important to notice that our equation is unsolvable. Since we can't divide by zero, all we need to write in this case is:

=undefined= undefined

And that's it! Hopefully you can now appreciate the simple power of trigonometric ratios. For more practice, visit this link here.