Reflections and rotations of shapes
Topic Notes
In this lesson, we will learn:
- How to draw reflections on a grid with vertical, horizontal, or diagonal mirror lines
- How to find order of rotational symmetry for shapes with multiple symmetry lines
- How to rotate shapes around a point 90°, 180°, 270°, and 360° clockwise or counter-clockwise
Notes:
- For line symmetry, a mirror test check if reflected halves match
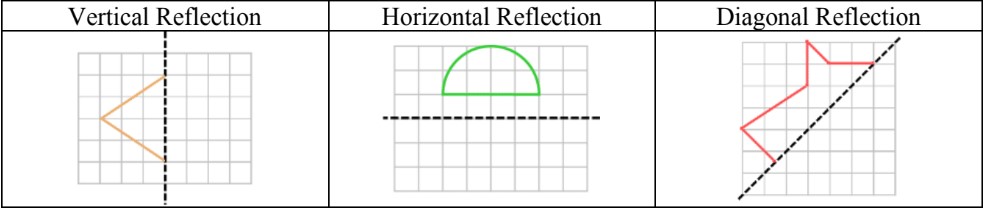
- When drawing reflections of shapes, a grid and a line of symmetry are used
- For reflections, the line of symmetry will be called the “mirror line” instead
- There can be vertical, horizontal, and diagonal mirror lines
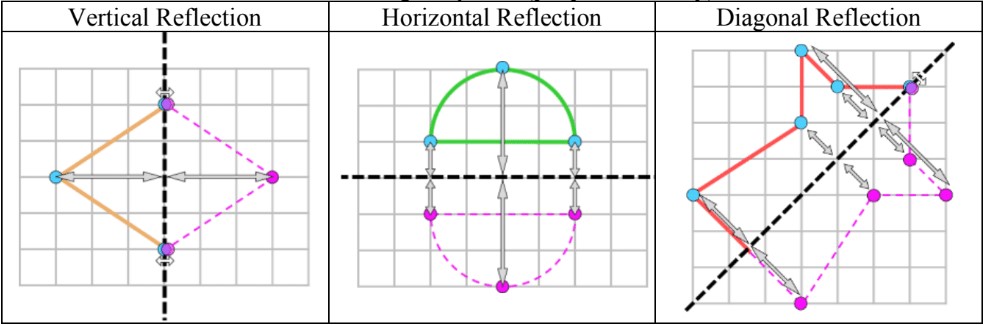
- Choose some exact points of the original shape on the grid
- To draw the reflection of these points, they must be the same distance away from the mirror line as the original points (perpendicularly)
- Another type of symmetry is called rotational symmetry
- If a shape has multiple lines of symmetry: when you spin it around in a full circle (360°), it will look exactly the same more than once
Ex. a triangle has 3 lines of symmetry; rotating a full circle, it matches the original 3 times

- Therefore, the order of rotational symmetry for this regular triangle is = 3
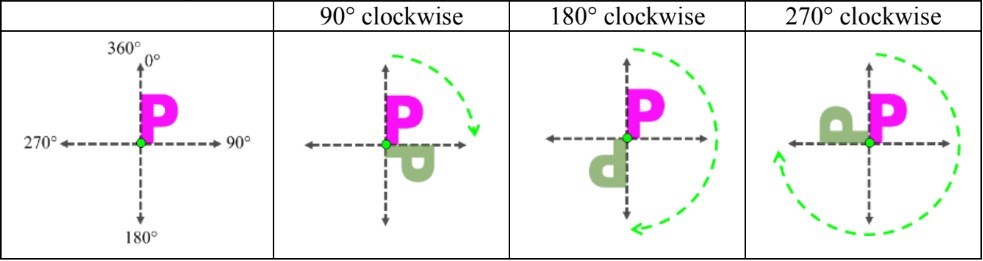
- When rotating shapes, the shape will be spun around a point (usually the middle):
- either clockwise or counter-clockwise
- To one of 4 main rotation angles: 90°, 180°, 270°, and 360°
Ex. Rotate the shape of the letter “P” clockwise 90°, 180°, and 270° around the point