Using models to add and subtract fractions
Topic Notes
How to add fractions
Before we begin this chapter, make sure you've got a good grip on prime factorization and divisibility rules.
When adding fractions, the first thing you'll have to do is make sure you have common denominators. This means that the number at the bottom of your fractions have to be the same. If your denominators aren't the same, you'll have to convert them so that they are.
You can get common denominators by taking the LCM (least common multiple) of the numbers in your denominator. Then you'll be able to add the numerators as you would with regular numbers when you carry out addition.
How to subtract fractions
When subtracting fractions, you'll also have to make sure that the denominators are the same. After you've found the common factors for the denominators, you can once again carry out subtraction.
Let's try out practice problems to see how this works. We'll demonstrate the concept using models to add fractions and using models to subtract fractions. This means you'll learn how to visually add and subtract fractions.
Example problems
Question 1:
Use a number line to calculate. Write the answer in lowest terms.
Solution:
So let's first draw the number line. Look at it and you see the number line from 0 to 1 is divided into 7 sections. This is because we are dealing with a denominator of 7

If the denominator is 7, one way to represent 1 in fraction form is = 1. With the number line in 7 sections, we can calculate on the number line:
Look at , it is on this location of the number line

And we are adding , and that's the result
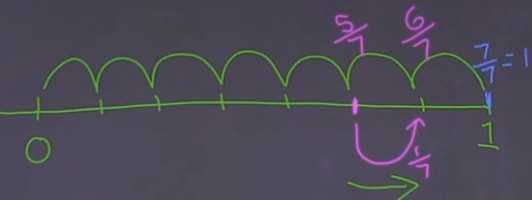
And our final answer is
Question 2:
Use a number line to calculate. Write the answer in lowest terms.
Solution:
So, let's draw the number line again. Look at it and you'll see the number line from 0 to 1 is divided into 8 sections. This is because we are dealing with a denominator of 8

If the denominator is 8, one way to represent 1 in fraction form is = 1. With the number line in 8 sections, we can calculate on the number line:
Look at , it is on this location of the number line
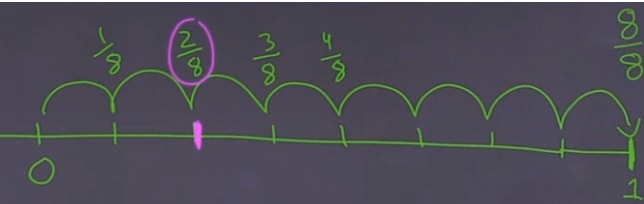
And we are subtracting , and that's the result
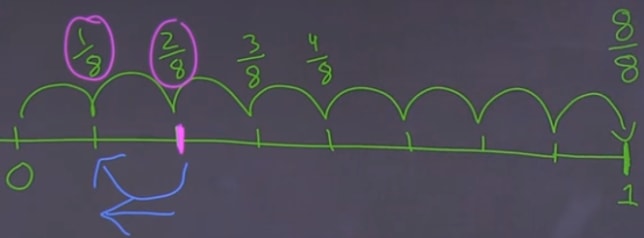
And our answer is
Question 3:
Write the addition or subtraction statement for the diagram. Write the answer in the lowest terms.
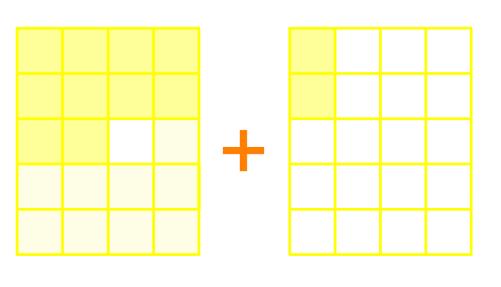
Solution:
We see the plus sign. So we are dealing with an addition. Each of the large rectangles represents a fraction. Each rectangle is divided into 20 sections. So 20 is the denominator. The shaded area represents the nominator.
So the first box:

It represents
And the second box:

It represents
So,
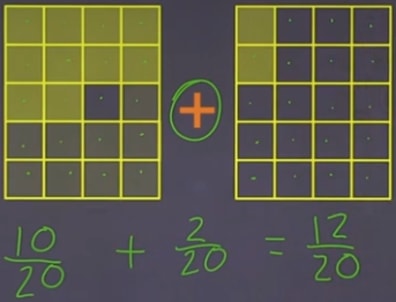
The question asks us to write the answer in the lowest terms. So, we need to look for the common factor of 12 and 20 in order to simplify the answer. Turns out 4 is the common factor. So, we'll divide 4 to the answer,
So
is the final answer.
Question 4:
Write the addition or subtraction statement for the diagram. Write the answer in the lowest terms.
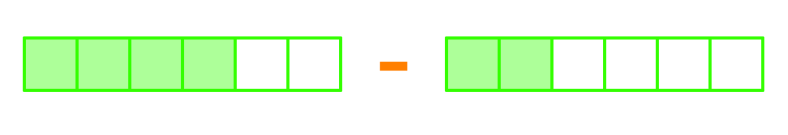
Solution:
We see the minus sign. So we are dealing with a subtraction. Each of the rectangles represents a fraction. Each box is divided into 6 sections. So 6 is the denominator. The shaded area represents the nominator
So the first box:

It represents
And the second box:

It represents
So,
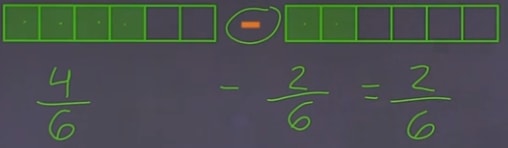
The question asks us to write the answer in the lowest terms. So, we need to look for the common factor of 2 and 6 in order to simplify the answer. Turns out 2 is the common factor. So, we divide 2 to the answer,
So
is the final answer.
Want to see an interactive diagram to see more of how to subtract fractions using a number line? Try this one out!
Next up, learn how to multiply whole numbers and fractions, and divide fractions with whole numbers. You can also learn how to multiply proper fractions.

