Probability with Venn diagrams
Topic Notes
Venn Diagrams can be a useful tool to represent and solve probability questions
Sample space: All possible outcomes of an experiment
Union(, "or"): AB is the event that either A occurs or B occurs or they both occur
Intersection (, "and"): AB is the event that both A occurs and B occurs
Addition Rule: A shortcut formula to finding is: AB = A + B – AB
Complement : All outcomes EXCEPT the event
Sample space: All possible outcomes of an experiment
Union(, "or"): AB is the event that either A occurs or B occurs or they both occur
Intersection (, "and"): AB is the event that both A occurs and B occurs
Addition Rule: A shortcut formula to finding is: AB = A + B – AB
Complement : All outcomes EXCEPT the event
Probability with Venn diagrams
What is a Venn diagram?
We define Venn diagram as a graphic representation of a group of sets of items (or possible outcomes) where the way each set is related to the others in the diagram can be clearly seen. The sets are always presented as either circles or closed curves, and they overlap with one another when their characteristics are shared, or when the items in one set belong to another too.
Confusing? Just take a look at the Venn diagram example below:
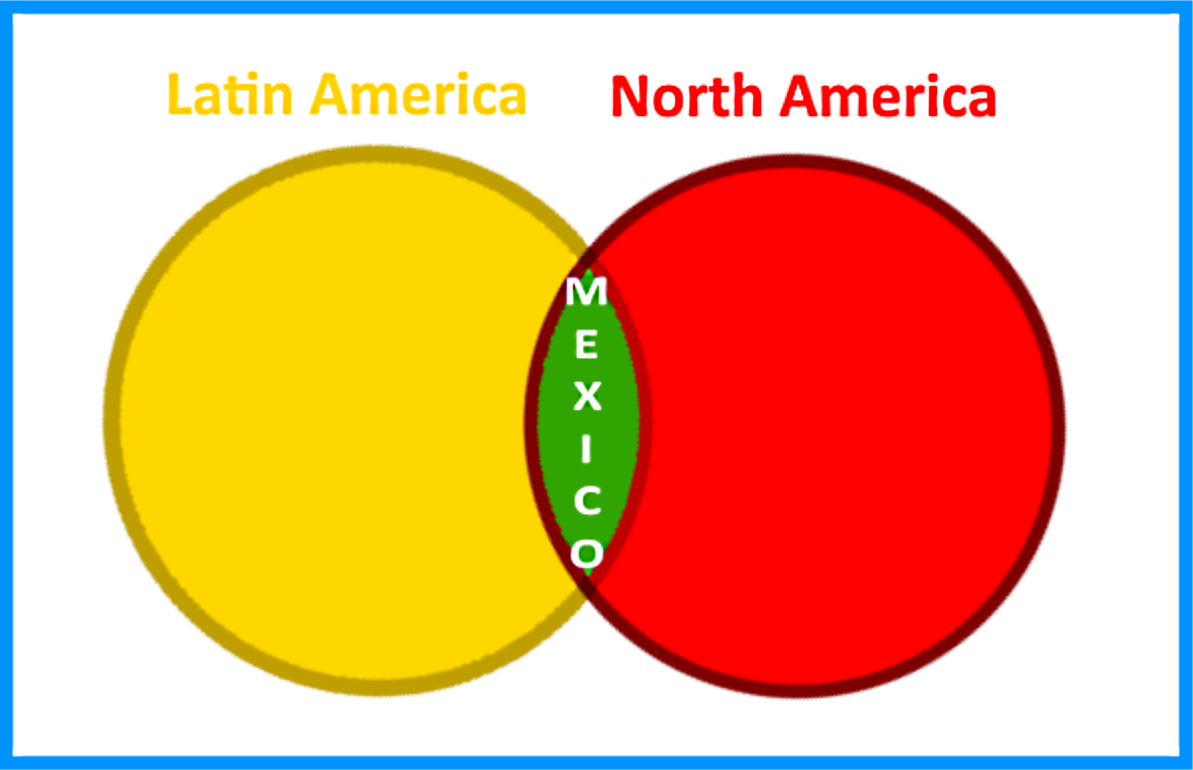
In this 2 circle Venn diagram we can see the composition of the American continent, and divide it between North America and Latin America. Notice that there is a piece of North America which is also part of Latin America, and that is Mexico! (Yes, Mexico is part of North America). Therefore, you can see how a Venn diagram shows the relationship between sets (in this case the two sets are North and Latin America) by depicting them as circles, and whenever an item from a set belongs to other, these circles will overlap.
Venn Diagrams can be a useful tool to represent and solve probability questions. In order to understand what a Venn diagram is and represents in a clearer manner, we have to remember the following details:
- A sample space: All possible outcomes of an experiment
Therefore, the sample space is the complete box surrounding the circles (or closed curves) that represent the sets.
- Union (, "or"): is the event that either A occurs or B occurs or they both occur.
- Intersection (, "and"): is the event that both A occurs and B occurs
- Addition Rule:
A shortcut formula to finding is:
More on the addition rule will be said in the next lessons. And the basic process will be explained on the Venn diagram problems in the last section of this lesson.
- Complement ():
Venn diagram problems
Using the Venn diagram definition from our first section, resolve the next example problems.Example 1
Looking at Venn diagrams for the representation of events, check out the next example problem: Out of a school of 100 students the number of students enrolled in PE and Band class is given below: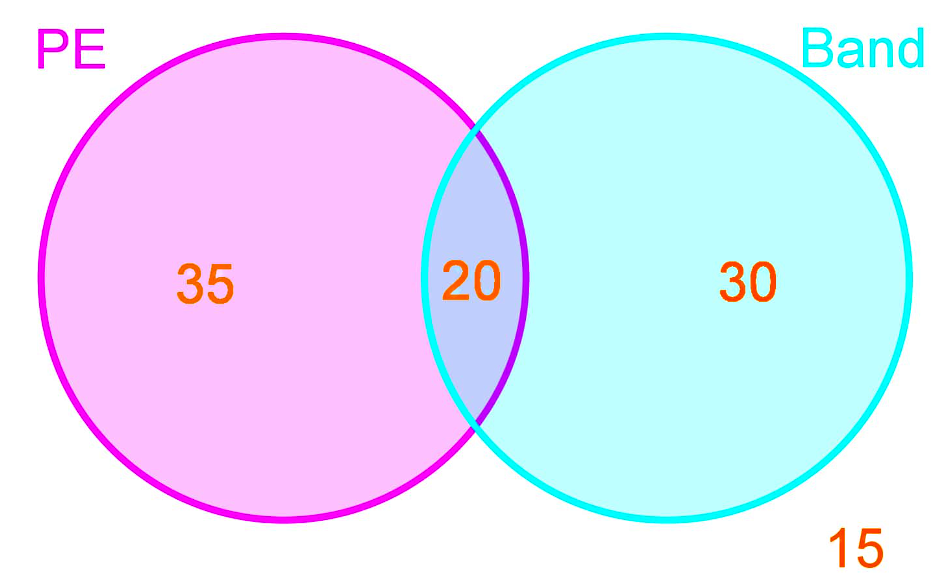
So there are 35 students who are taking only PE classes, 30 students who are taking only Band classes, and 20 students who are taking both PE and Band classes. There are also 15 students who are not enrolled in PE or Band classes.
1. Replicate this Venn diagram in terms of probabilities of picking a random student from any of these classes.
In this case we have the next classes:
- PE (Physical education) class = 35 students.
- Band class = 30 students.
- Both PE and Band = 20 students.
- Not enrolled = 15 students.
Therefore, we have a total of: 35 + 30 + 20 + 15 = 100 students, as mentioned in the problem. This total of students is the complete sample space; and so, the probabilities for each class are:
- P(PE) = 35/100
- P(Band) = 30/100
- P(Both PE and Band) = 20/100
- P(Not enrolled) = 15/100
Meaning that each class has a certain amount of students out of 100, and thus the Venn diagram probability depiction goes as:
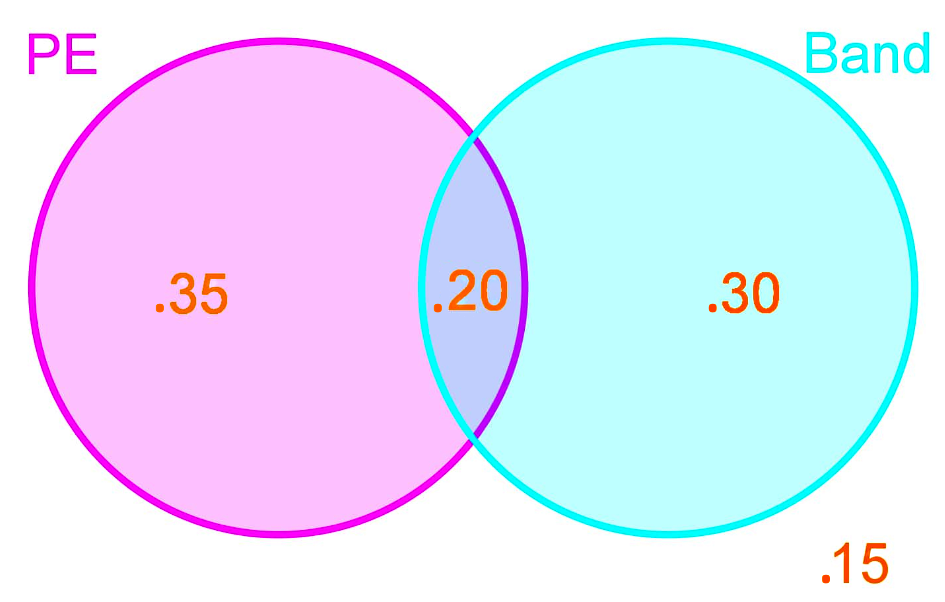
Where all of the sample space is represented as everything inside the box on the diagram, and has a probability of 1. And each of the classes we have listed, has its probability marked in each of their corresponding areas.
2. What is the probability of picking a student who is in PE class?
We already know that the probabilities of choosing a student enrolled in PE class ONLY, is equal to 0.35. While the probability of picking a student that is enrolled in both PE and Band is equal to 0.20. If you think about it (and noticing from figure 2) there are a total of 55 students out of 100 who are taking PE class (either by itself, or with another class).
Therefore, our total probability of picking a student who is enrolled in PE class is equal to 55/100 or 0.55.
Example 2
On this problem we take a look at how to use unions and intersections in Venn diagrams.The following dots represent students who attend each after school activity:
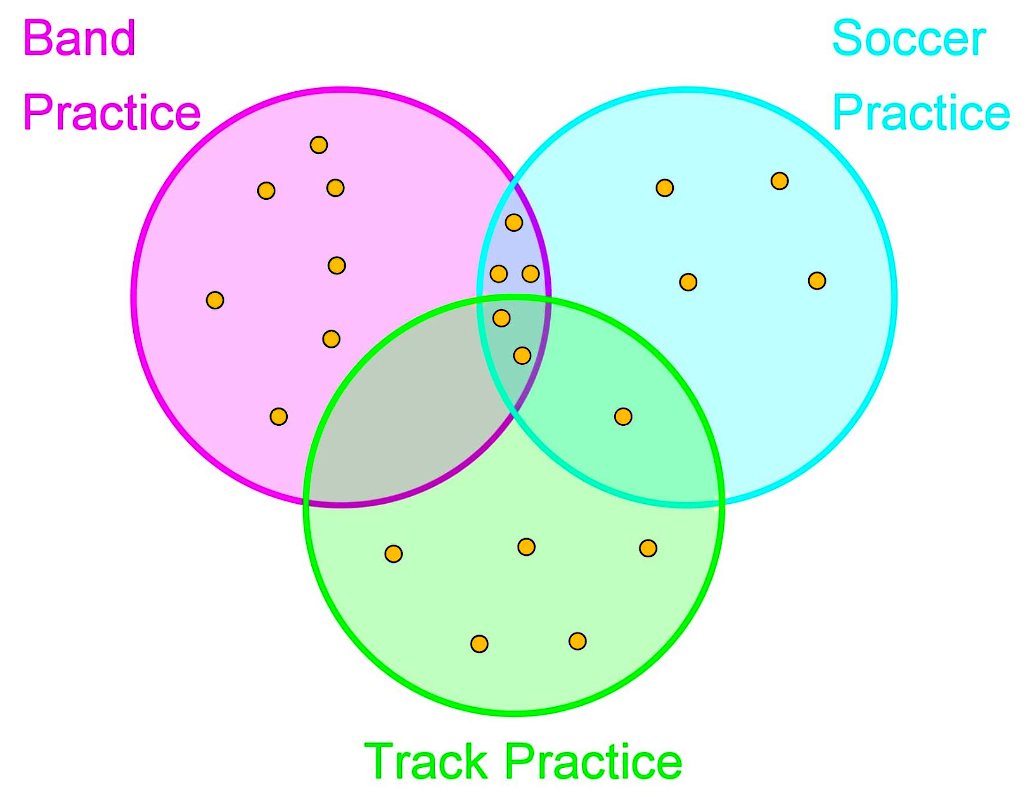
1. How many students attend only Band Practice, what is the probability of picking a student who attends only Band Practice?
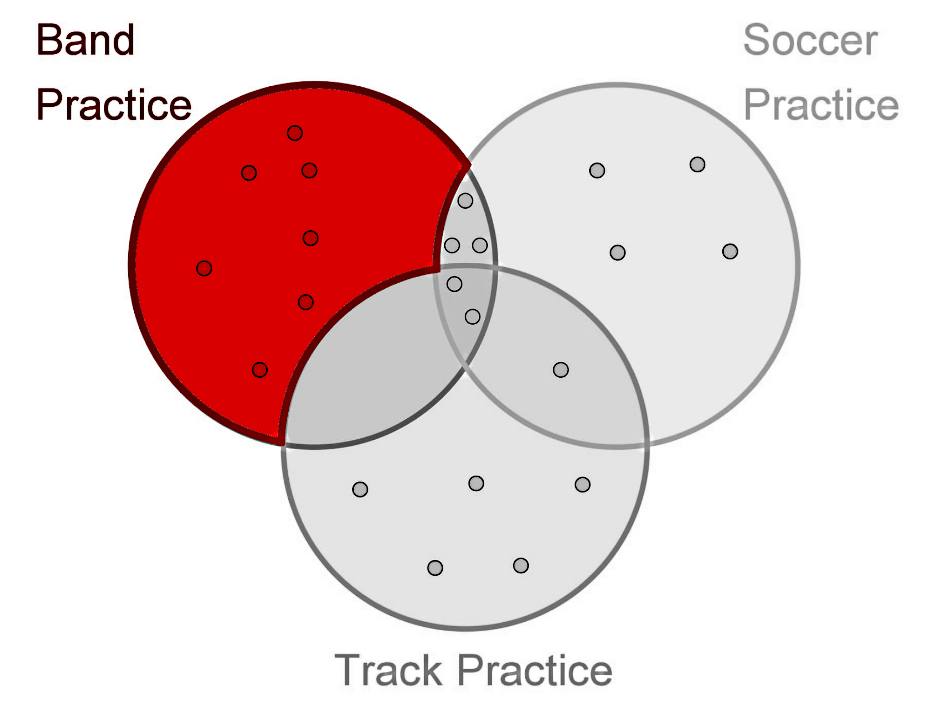
By counting the dots on the triple Venn diagram in figure 4, we notice that there are a total of 22 students in the whole diagram. These 22 students are the complete sample space.
Therefore, since there are only 7 dots in the area belonging to Band practice ONLY, we have that there are 7 students out of a total of 22, who attend Band practice as their only activity in the afternoons, after school. And so, the probability of picking a student who attends only band practice in the afternoons is equal to: = 7/22 = 0.3181818.
Such probability belongs to this area on the 3 circle Venn diagram:
2. How many students attend Soccer Practice AND Band Practice, what is the probability of picking these students?
For this question the key word is and, therefore, we are looking for students attending soccer AND band, or, the intersection of the regions for soccer practice and band practice depicted in the Venn diagram as follows:
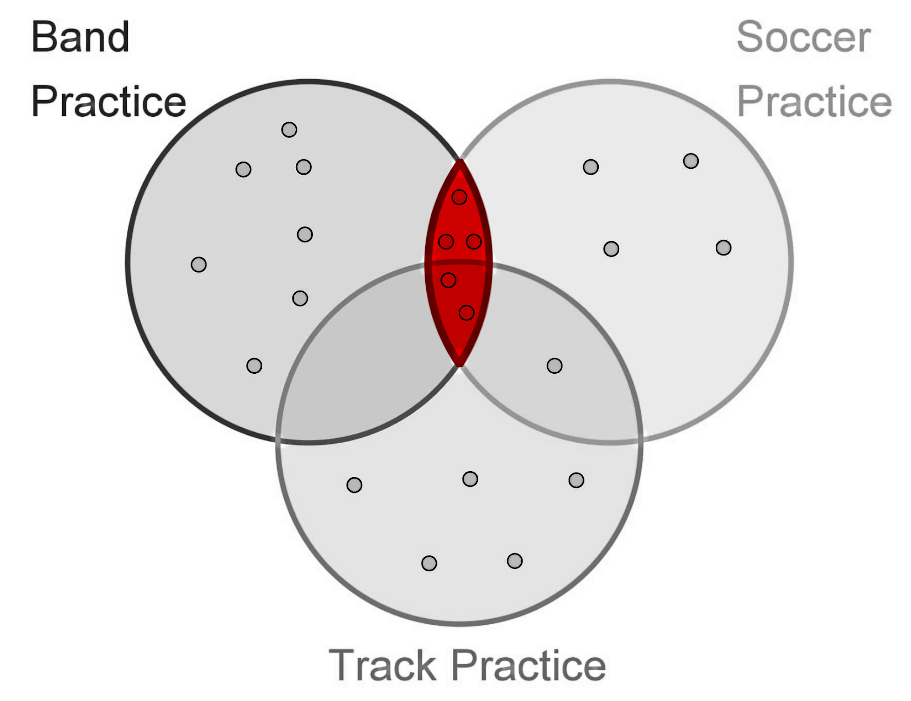
Counting the amount of students belonging to the (intersection of Band and Soccer) region as marked above, we have that there are a total of 5 students who attend both band and soccer practice after school, and so, the probability of picking one of these students out of the total of 22 is equal to = 5/22 = 0.227272.
3. How many students attend Soccer Practice AND Band Practice AND Track Practice, what is the probability of picking these students?
In this case, we are asked to find out how many students belong to the intersection of the regions for all three: band, soccer and track practices. Shading that intersection in the Venn diagram, we find that:
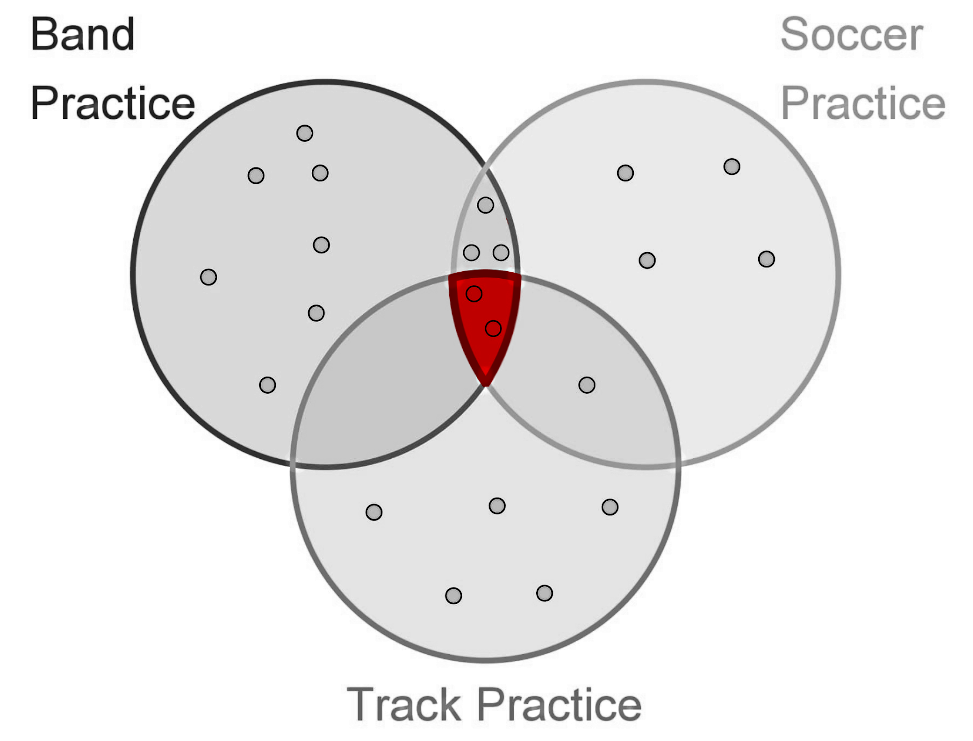
Therefore, we can clearly see that the amount of students in the intersection is equal to 2. And the probability of picking one of these 2 students out of the total of 22 is equal to: = 2/22 = 0.09091.
4. How many students attend Track Practice OR Soccer Practice, what is the probability of picking these students?
Looking for the students that attend track practice OR soccer practice, means we are looking for the students belonging to the union denoted by . Which is denoted in the next figure in red:
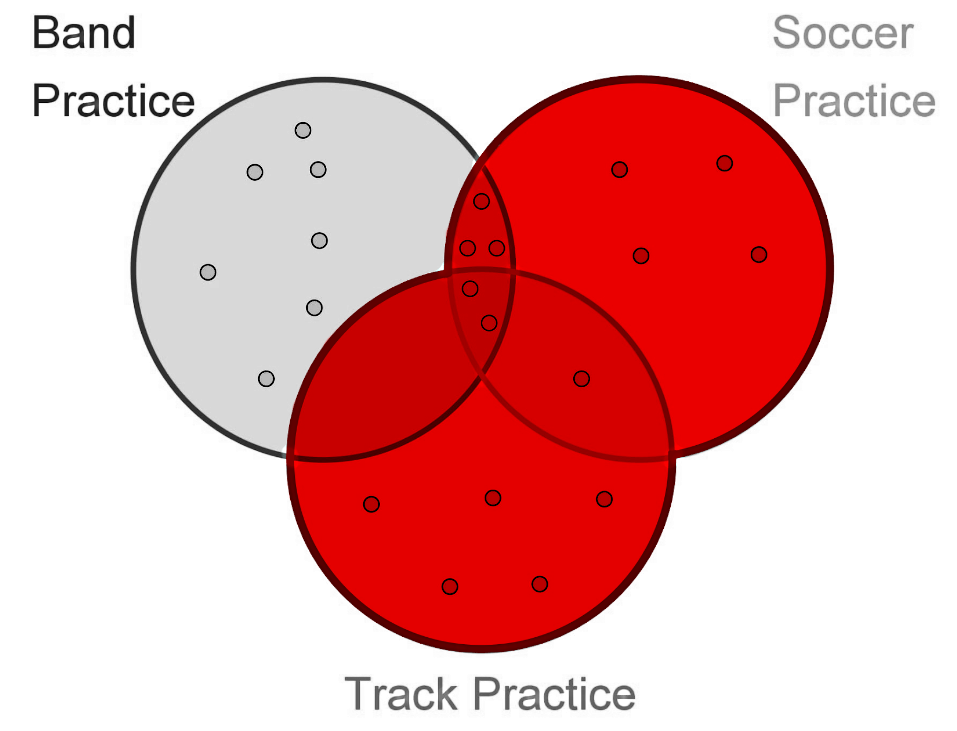
And so, counting the dots in the region for the union of track and soccer practices, we have that there are a total of 15 students who attend track and soccer. Thus, the probability of picking one of these students is equal to: = 15/22 = 0.681818
5. How many students attend Band Practice OR Soccer Practice, but not Track Practice? What is the probability of picking these students?
Once more we are looking for the students in a union, but this case, the union of band and soccer practices:
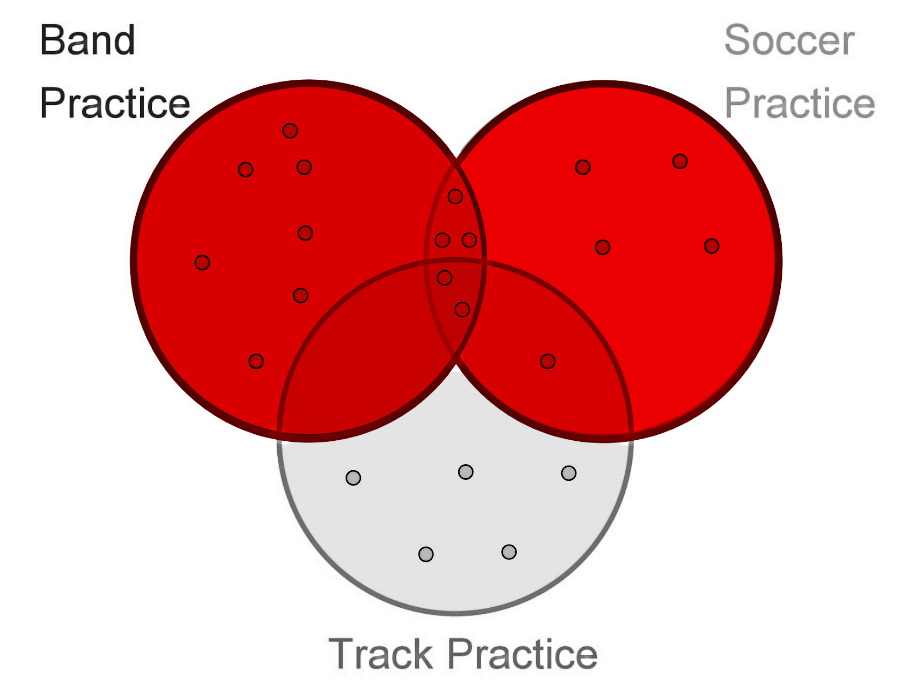
Counting the dots in the region for the union of band and soccer practices, we have that there are a total of 17 students who attend track and soccer. Thus, the probability of picking one of these students is equal to: = 17/22 = 0.772727
Example 3
This next problem is dedicated to the addition rule, for extended details on the addition rule take a look at our next lesson on addition rule for OR.From a deck of cards, 10 cards are drawn at random. From these 10 cards the probability of picking a king is 0.3 and the probability of picking a heart is 0.5. The probability of picking a card that is both a king and a heart (the king of hearts) is 0.1.
1. Represent these probabilities as a Venn Diagram
Let us think about the information provided above in order to answer this question. The sample of cards we are looking at consists of 10 cards, from which, if we are to pick a card at random, there is a probability of 3 out of 10 to select a king, and a probability of 5 out of 10 to select a heart. From those, there is the probability of 1 out of 10 to select the king of hearts (meaning that the king of hearts is present in the 10-card sample.
With that in mind, we can conclude that our sample of 10 cards contains: 2 kings and 4 cards that have the heart symbol different from the king of hearts, the king of hearts, and three cards that are left which can be anything but a king or a heart.
And so, we make a Venn diagram from such a sample, and the result is shown below:
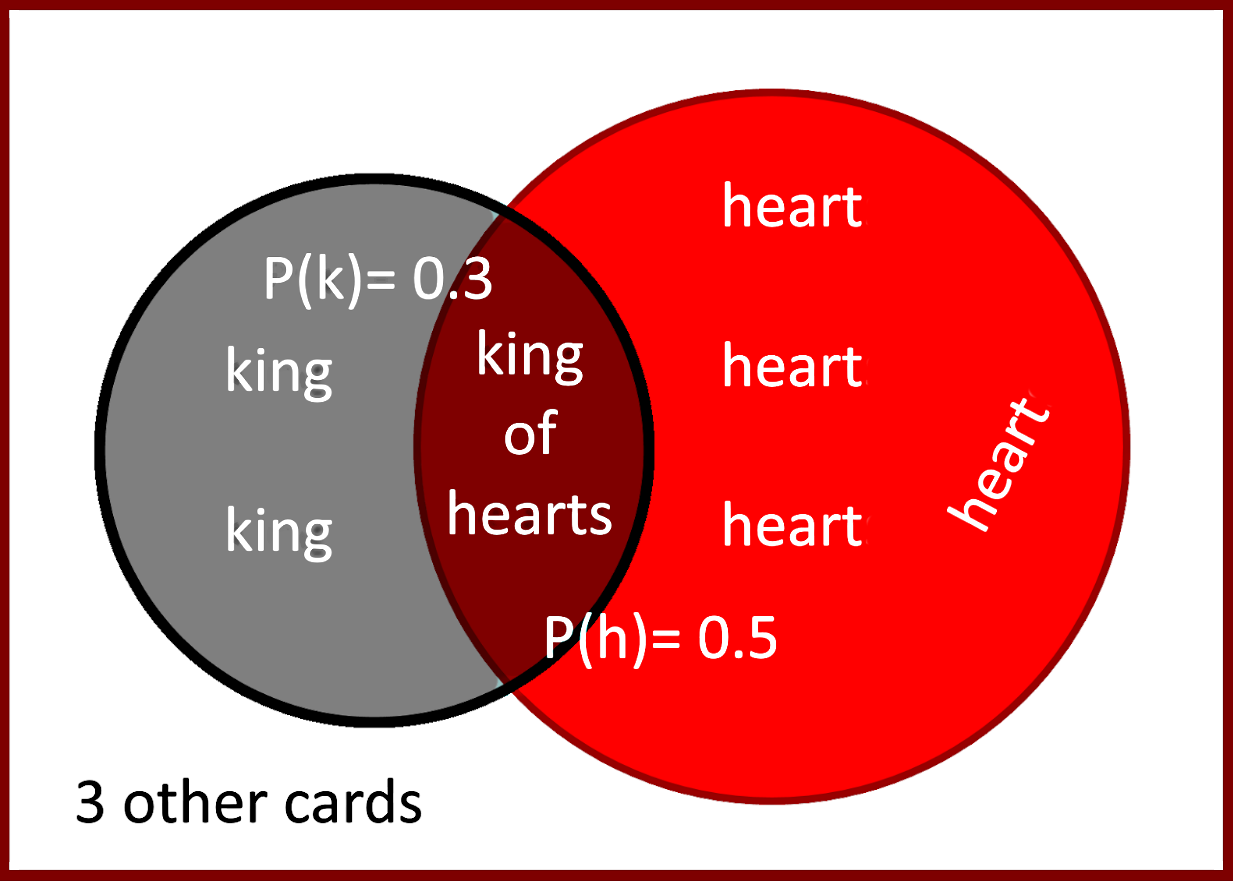
Notice that the circle representing the hearts is bigger than that representing the kings, that is because we have more hearts than kings. Also notice that the sample space contains 3 other cards which are not hearts or kings.
2. What is the probability of picking a king that isnt a heart?
Out of the ten cards drawn, there are only two king cards which are not hearts; therefore, there is a probability of (King other than king of hearts)= 2/10 = 0.2.
3. What is the probability of picking a heart that isnt a king?
Out of the ten cards drawn, there are only four heart cards which are not kings; therefore, there is a probability of (Heart card other than king of hearts) = 4/10 = 0.4.
Notice that the probabilities in the Venn diagram are not the same as the ones answering questions 2 and 3; this is because the probabilities in the Venn diagram are for everything that is inside either the black circle or the red circle.
- P(k)=0.3 for everything inside the black circle.
- P(h)=0.5 for everything inside the red circle.
4. What is the probability of picking a king OR a heart?
In this case, we are asked to find the probability of a card being picked from the union of the king and heart cards. Therefore, the probability is equal to for which we use the addition rule formula ; and we have that:
Example 4
The probabilities of certain events are given in the Venn Diagram below: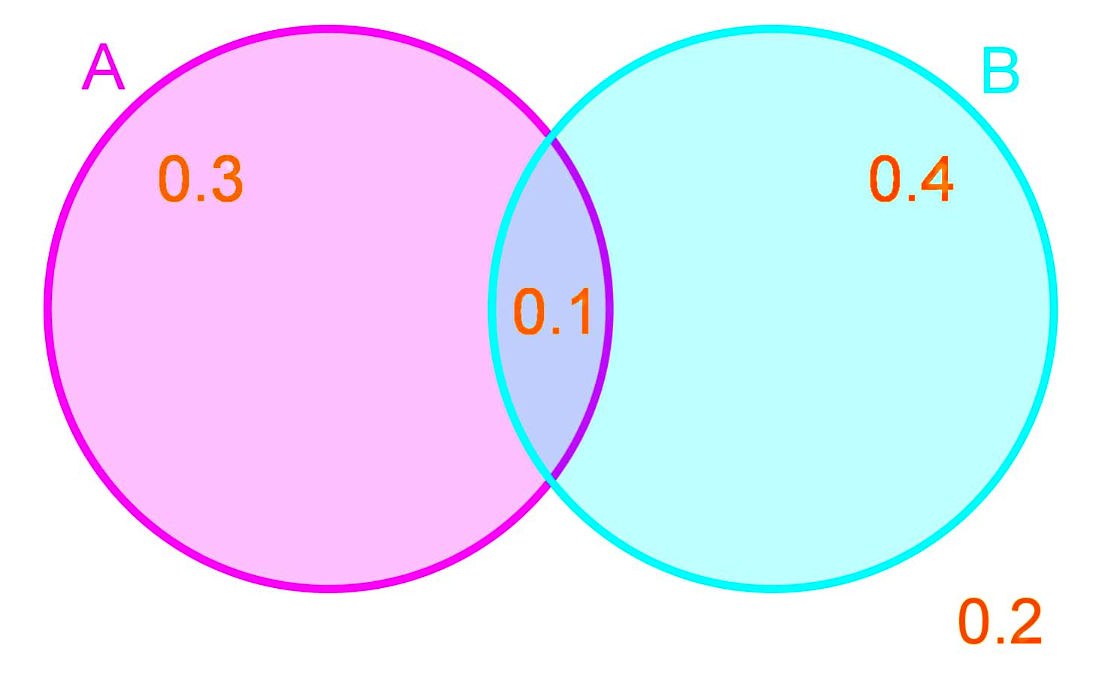
1. What is the probability of A occurring?
A accounts for everything inside the left circle, therefore, the probability of that total is equal to the addition:
2. What is the probability of A NOT occurring?
The probability for anything inside the sample space to occur is equal to 1 (the total probability for all the regions accounted for). Therefore, the probability for not occurring is to obtain the probability of the complement of , and goes as follows:
3. What is the probability of occurring or occurring?
The probability of occuring OR occurring is equal to the union of and , and therefore, we calculate it as follows:
4. What is the probability of neither nor occurring?
We follow the same logic as in question 2, and know that, since the total probability is equal to 1, then the probability for neither nor occurring is equal to:
This is the end of our lesson. Before we pass onto the next lesson we recommend you to take a look at this handout of probability problems, where you will find some useful Venn diagram examples that can be useful for you to practice even more.
We hope you have enjoyed the lesson of today, see you on the next!

