Multiplying fractions and whole numbers
Topic Notes
- Multiplying Fractions and Whole Numbers Involving Single-digit Numbers
- Word Problems: Application of Multiplying Fractions and Whole Numbers
- Multiplying Fractions and Whole Numbers Involving Multiple-digit Numbers
What is a whole number
You've encountered lots of whole numbers before now. Whole numbers are numbers that aren't fractions—they are integers. For example, , and would all be whole numbers.
On the other hand, numbers that aren't whole numbers would look something like or . Although a fraction is a rational number, it is not a whole number. Knowing the difference will be important in this lesson
How to multiply fractions with whole numbers
When you're given a question that requires you to deal with multiplying fractions with whole numbers, there's main steps you'll have to carry out.
Firstly, rewrite the question so that the whole number is turned into a fraction. As you probably already know, when you have a whole number, turning it into a fraction just requires you to put it over . So for example, if you wanted to convert into a fraction, it'll be rewritten as .
Secondly, multiply the two numerators in the two respective fractions. This just means taking the two numbers on top of each of the fractions and then multiplying them with one another.
For the third step, do the same as step two but now you're using the two numbers in the denominators in the fractions. You'll end up with a new fraction after doing steps two and three!
Lastly, you'll just have to simplify the fraction you've gotten after solving the problem. You have to show your answer in the lowest terms possible, or you may get marks deducted for not having completely finished the question. Let's take a look at some examples and put the four steps into use to help you with multiplying fractions and whole numbers.
Practice problems
Question 1:
Calculate
Solution:
First, we can express as a fraction:
Our question will then be converted to something that looks like this:
We multiply these fractions, first tackling the top numbers () and then doing the bottom ones (). Then we'll get our final number, which is a new fraction.
Since is already the most simplified form of the fraction, this will be your final answer.

Question 2:
A pizza had slices, and of it was eaten in a party. How many slices of pizza were eaten during the party?
Solution:
There were slices and were eaten. So we multiply and to get the answer. Let's express as a fraction.
Before doing multiplication, we can simplify the question first and get this:
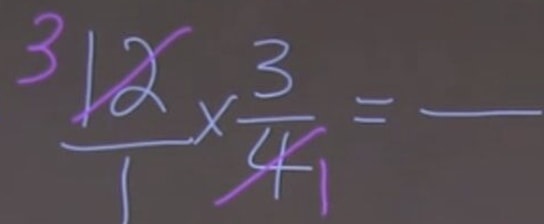
Now, do the multiplication. We've got as the final answer
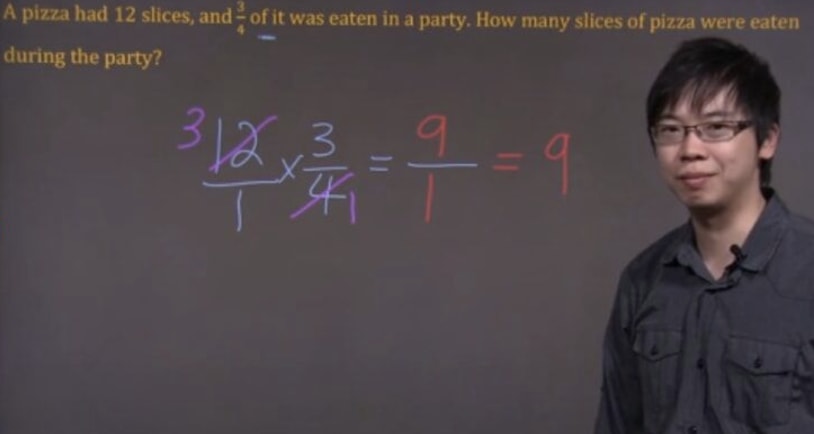
If you're ever unsure about your answer in questions involving the multiplication of whole numbers and fractions, use this calculator to help you double check your work.
Good lessons to review and move forward with to help you understand this lesson better includes finding common factors, comparing rational numbers, and solving problems with rational numbers in fraction form. These will eventually lead you into the more advanced problems of solving two-step linear equations.

