Counting backwards
Topic Notes
In this lesson, we will learn:
- How do we count backwards using: the numbers 9 to 0, number lines (and negative numbers), and big numbers (up to millions)?
- Counting Backwards can help us write subtraction statements.
Notes:
- We use numbers to represent how many things there are.
- You can do the exact opposite of normal counting by counting BACKWARDS:
- 10, 9, 8, 7, 6, 5, 4, 3, 2, 1…
- Counting backwards means the counting numbers are getting SMALLER
- If you look at a number line, counting forwards means going from right to left
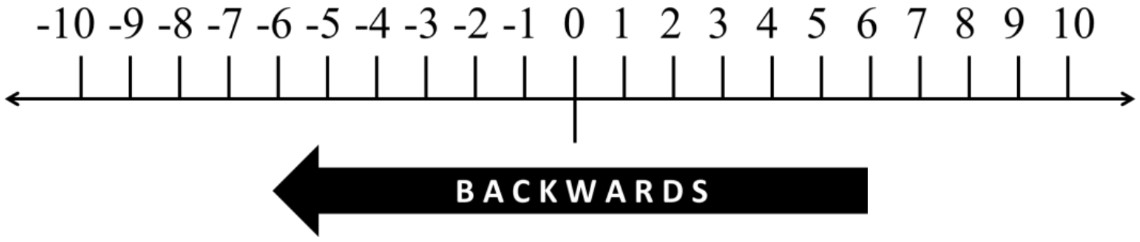
- Negative numbers also count backward by going from right to left on a number line
- Don’t get confused! The negative numbers (digits) are going forwards, but they have a negative sign!
- The bigger your negative, the smaller your value (more negative = smaller)
- Ex. counting backwards in negatives: -1, -2, -3, -4, -5, …
- Recall: number PLACE VALUES!

- The smaller place values are on the right, the bigger place values are on the left
- When the digit decreases (from 9 to 0): after you hit 0, next you will decrease 1 FROM the place value on the left. Your digit will then start again from 9 (and count down to 0, repeating the process)
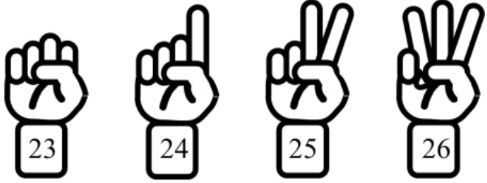
- You can also use your fingers to count backward and find out how many numbers you have decreased (counted down) by.
- Put down all your fingers (zero fingers up) when you start on your first number.
- Each number you count down, raise one more finger.
- When you reach your last number, you can count your raised fingers
- Ex. counting from 32 down to 27: you count down by five
- This can allow you to make subtraction statements!
- [starting #] – [how much you counted down] = [last #]
- Ex. counting from 32 down to 27, the subtraction statement is: 32 – 5 = 27
Introduction to Counting Backwards
Counting backwards is a fundamental mathematics skill that builds on a child's understanding of numbers and their sequence. Our introduction video serves as an engaging starting point, demonstrating this concept in a fun and interactive way. By watching, children can visualize the process of moving backwards along the number line. This skill is crucial in mathematics as it lays the foundation for subtraction, mental math, and problem-solving. Counting backwards helps develop number sense, improves memory, and enhances cognitive flexibility. It's particularly useful in everyday situations like countdown timers or calculating change. As children master counting backwards, they gain confidence in manipulating numbers and develop a deeper understanding of numerical relationships. This skill also prepares them for more advanced mathematical concepts, making it an essential part of early mathematics education. Practice and repetition are key to mastering this important skill.
Understanding the Basics of Counting Backwards
Counting backwards is a fundamental mathematical concept that involves moving through a number sequence in reverse order. This skill is essential for various real-life situations and forms the basis for more advanced mathematical operations. Unlike counting forwards, which starts from a lower number and progresses to higher ones, counting backwards begins with a larger number and moves towards smaller ones.
To illustrate the concept of counting backwards, let's consider a practical example using donuts. Imagine you have a box of 12 donuts, and you start eating them one by one. As you consume each donut, you're essentially counting backwards. You begin with 12 donuts, then you have 11, then 10, and so on. This real-life scenario demonstrates how counting backwards naturally occurs in everyday situations.
The donut example highlights the difference between counting forwards and backwards. When counting forwards, you would start with zero donuts and add them one by one until you reach 12. In contrast, counting backwards starts with the total number of donuts (12) and decreases with each donut eaten. This reverse process is what makes counting backwards unique and valuable in various contexts.
Understanding the digits used in counting backwards is crucial. The sequence typically involves the numbers 9 to 0, which are used repeatedly as you move through larger numbers. For instance, when counting backwards from 100, you would use these digits in descending order: 9, 8, 7, 6, 5, 4, 3, 2, 1, 0. Once you reach 90, the cycle repeats with 89, 88, 87, and so on.
Counting backwards requires a strong grasp of number relationships and place value understanding. As you move from one number to the next, you need to understand how the digits change. For example, when counting backwards from 20, you'll encounter the transition from 20 to 19, where both digits change simultaneously. This concept becomes more complex with larger numbers, making it an important skill to develop.
The ability to count backwards has numerous practical applications. In addition to the donut example, it's used in various scenarios such as countdown timers, calculating change in money transactions, and even in simple games. Moreover, counting backwards is a foundational skill for mental math, helping individuals perform quick calculations without relying on written methods or calculators.
To practice counting backwards, start with small number sequences and gradually increase the difficulty. Begin with counting backwards from 10 to 0, then try larger numbers like 20 or 50. As you become more comfortable, challenge yourself with three-digit numbers or even start from random points within a sequence. Regular practice will improve your speed and accuracy in counting backwards.
It's worth noting that counting backwards is not just about memorizing a reverse sequence. It involves understanding the logical progression of numbers and how they relate to each other. This deeper comprehension aids in developing overall number sense and mathematical fluency, which are crucial for more advanced mathematical concepts and problem-solving skills.
In conclusion, counting backwards is a vital mathematical skill with real-world applications. From the simple act of eating donuts to more complex calculations, this concept plays a significant role in our daily lives. By mastering the digits used in counting backwards and understanding the differences between forward and backward counting, individuals can enhance their mathematical abilities and problem-solving skills. Regular practice and application in various contexts will solidify this fundamental concept, paving the way for more advanced mathematical understanding and place value understanding.
Counting Backwards on a Number Line
A number line is a powerful visual tool for understanding mathematical concepts, including counting backwards. This skill is essential for developing a strong foundation in arithmetic and preparing for more advanced mathematical operations. When counting backwards on a number line, we move to the left, which is the opposite direction of counting forward.
To use a number line for counting backwards, start by identifying your starting number. Let's say we begin at 10. Visualize this number on the line, typically represented as a point or a small vertical mark. To count backwards, we'll move to the left of this point, decreasing by one with each step. For example, counting backwards from 10 would look like this: 10, 9, 8, 7, and so on.
The left direction on the number line is crucial when counting backwards. Each step to the left represents a decrease of one unit. This leftward movement is consistent whether we're dealing with whole numbers and decimals. Understanding this directional concept helps students grasp the idea that numbers become smaller as we move left on the number line.
Practicing counting backwards on a number line can improve mental math skills and number sense. It's particularly useful when learning subtraction, as the process of counting backwards is essentially subtracting one at a time. For instance, if we're solving 10 - 3, we can start at 10 on the number line and count back three steps to the left, landing on 7.
Counting Backwards with Negative Numbers
When we introduce negative numbers, counting backwards becomes even more interesting. Negative numbers are located to the left of zero on the number line. When counting backwards from positive numbers and crossing zero, we enter the realm of negative numbers.
For example, if we start at 3 and count backwards, we'd go: 3, 2, 1, 0, -1, -2, -3, and so on. Notice how we continue moving left even after passing zero. This continuous leftward movement helps students understand the relationship between positive and negative numbers.
Counting backwards with negative numbers differs from positive numbers in a few key ways:
- Direction: While we still move left, we're now increasing the magnitude of negative numbers. For instance, -2 is considered "less than" -1, even though 2 is greater than 1 in positive numbers.
- Zero crossing: When counting backwards from positive to negative, we pass through zero. This zero-crossing point is crucial for understanding the transition between positive and negative numbers.
- Magnitude: As we count backwards with negative numbers, the magnitude of negative numbers increases, but the actual value decreases. For example, -5 is less than -4, even though 5 is greater than 4.
Using a number line to visualize these concepts can greatly aid in understanding negative numbers. It helps students see that negative numbers continue infinitely to the left of zero, just as positive numbers extend infinitely to the right.
Practicing counting backwards with both positive and negative numbers on a number line reinforces important mathematical concepts. It helps develop a strong number sense, improves mental math skills, and prepares students for more advanced topics like algebra and coordinate geometry.
In conclusion, the number line is an invaluable tool for teaching and learning how to count backwards. By consistently moving left on the number line, students can visualize the process of decreasing values, whether dealing with positive or negative numbers. This visual representation helps solidify the abstract concept of counting backwards and provides a strong foundation for future mathematical learning.
Counting Backwards with Larger Numbers
Counting backwards with larger numbers is an essential skill in mathematics that builds upon the foundational concept of place value. This process becomes more complex as we move from two-digit to three-digit and four-digit numbers, introducing the need for borrowing across place values. Let's explore this concept in detail, using examples to illustrate the process.
Starting with two-digit numbers, counting backwards is relatively straightforward. For instance, when counting backwards from 50, we simply decrease the ones digit: 50, 49, 48, 47, and so on. However, when we reach 40, we need to adjust both digits: 39, 38, 37, etc. This introduces the concept of borrowing, where we "borrow" from the tens place to continue counting in the ones place.
Moving to three-digit numbers, the process becomes more intricate. Let's consider counting backwards from 100. We start with 100, 99, 98, 97, and continue until we reach 90. At this point, we need to borrow from the hundreds place: 89, 88, 87, and so forth. The real challenge comes when we reach a number like 200 and count backwards. We go from 200 to 199, which requires borrowing from the hundreds place to adjust both the tens and ones places.
The concept of borrowing becomes even more pronounced when dealing with four-digit numbers. Imagine counting backwards from 1000. We begin with 1000, 999, 998, 997, and continue until we reach 990. Then we borrow from the thousands place: 989, 988, 987, and so on. The process becomes particularly interesting when we encounter numbers that require multiple borrowing steps, such as counting backwards from 2000 to 1999.
To better understand the borrowing process, let's break down the step-by-step procedure when counting backwards from 2000 to 1999:
1. We start with 2000.
2. We need to decrease by 1, but we can't simply subtract 1 from 0 in the ones place.
3. We borrow from the tens place, but it's also 0, so we move to the hundreds place.
4. The hundreds place is also 0, so we finally borrow from the thousands place.
5. The 2 in the thousands place becomes 1.
6. The hundreds place becomes 9.
7. The tens place becomes 9.
8. The ones place becomes 9.
9. Thus, we arrive at 1999.
This example demonstrates how borrowing can cascade across multiple place values when counting backwards with larger numbers. It's crucial to understand this process as it forms the foundation for more advanced mathematical operations, such as subtraction with regrouping.
When practicing counting backwards with larger numbers, it's helpful to use visual aids or manipulatives to represent place values. This can make the borrowing process more tangible and easier to grasp. For instance, using base-ten blocks can visually demonstrate how a thousand block is broken down into hundreds, then tens, and finally ones as we count backwards.
As students become more comfortable with this concept, they can tackle more challenging exercises, such as counting backwards by specific intervals (e.g., counting backwards by 5s or 10s from a four-digit number) or solving word problems that involve backwards counting across large number ranges.
In conclusion, counting backwards with larger numbers is a fundamental skill that reinforces understanding of place value and prepares students for more complex mathematical operations. By mastering this process with two-digit, three-digit, and four-digit numbers, students develop a strong foundation for future mathematical concepts and problem-solving skills.
Practical Applications of Counting Backwards
Counting backwards is a fundamental skill that has numerous real-world applications and is closely related to subtraction. This essential mathematical concept is used in various everyday situations and forms the basis for more complex mathematical operations. Understanding how to count backwards efficiently can greatly improve one's ability to perform mental math and solve practical problems.
One of the most common real-world applications of counting backwards is in time management. For example, when setting a timer for cooking or scheduling tasks, we often need to count backwards from a specific time. This skill is also crucial in sports, where athletes and coaches need to keep track of remaining time in a game or match. In financial contexts, counting backwards is used when calculating change or determining how much money is left after expenses.
The relationship between counting backwards and subtraction is fundamental. When we count backwards, we are essentially performing repeated subtraction by one. This connection helps children understand the concept of subtraction more intuitively. For instance, when counting backwards from 10 to 7, we are subtracting 1 three times (10 - 1 - 1 - 1 = 7), which is equivalent to 10 - 3 = 7.
There are several methods for counting backwards, each with its own advantages. The finger counting method is particularly useful for young children or those new to the concept. Using the example of counting from 32 to 27, one would start by holding up three fingers on one hand (representing 30) and two fingers on the other (representing 2). As they count backwards, they would lower one finger at a time until reaching 27.
The jump method is another effective technique, especially for larger numbers or when counting backwards by more than one. In our example, one would start at 32 and make "jumps" backwards: 32 to 30 (jump of 2), then 30 to 27 (jump of 3). This method helps visualize the process on a number line and can be particularly useful when working with multiples.
The underlining method is a written technique that can be helpful for those who prefer visual aids. Starting with the number 32, one would underline the 2 (units digit) and count backwards: 31, 30, 29, 28, 27. This method helps keep track of the tens place while focusing on changing the units digit.
Practicing these methods can significantly improve one's ability to count backwards and perform subtraction mentally. It's important to choose the method that works best for individual learning styles and the specific situation at hand. For instance, the finger counting method might be more suitable for younger children, while adults might prefer the jump method for quick mental calculations.
In educational settings, teachers often use games and activities that incorporate counting backwards to make learning more engaging. These can include number line hopscotch, countdown rockets, or digital games that require quick backwards counting. Such activities not only reinforce the skill but also demonstrate its practical applications in a fun and interactive way.
As students progress, they can apply these backwards counting skills to more advanced mathematical concepts. For example, understanding how to count backwards is crucial when learning to borrow in subtraction or when working with negative numbers. It also forms the foundation for understanding concepts like counting down in algebra or working with reverse sequences in more advanced mathematics.
In conclusion, counting backwards is a versatile skill with numerous real-world applications. Its close relationship to subtraction makes it a fundamental concept in mathematics education. By mastering different methods like finger counting, the jump method, and the underlining method, individuals can improve their mental math abilities and problem-solving skills. Whether in everyday situations or academic settings, the ability to count backwards efficiently is an invaluable tool that enhances mathematical proficiency and practical problem-solving capabilities.
Common Challenges and Tips for Counting Backwards
Counting backwards is an essential skill that many students struggle with, but it's crucial for developing strong mathematical foundations. This article will address common difficulties students face when learning to count backwards and provide effective tips and strategies to overcome these challenges.
One of the primary challenges students encounter is the mental shift required to think in reverse. Unlike counting forward, which feels more natural, counting backwards demands a different cognitive approach. To address this, encourage students to visualize a number line in their minds, moving from right to left as they count down.
Another common difficulty is maintaining focus and avoiding errors, especially with larger numbers. To combat this, break the task into smaller, manageable chunks. For instance, when counting backwards from 100, focus on decades (100, 90, 80) before tackling individual numbers within each decade.
Students may also struggle with transitioning between decades or hundreds. Practice exercises focusing specifically on these transitions can be helpful. For example, count backwards from 31 to 29, or from 102 to 98, to reinforce these challenging points.
To improve counting backwards skills, incorporate the following mental math techniques and practice exercises:
- Skip counting: Practice counting backwards by 2s, 5s, or 10s to build familiarity with number patterns.
- Number line jumps: Use a physical or imaginary number line to visualize backwards movements.
- Countdown games: Create fun, timed activities where students race to count backwards from a given number.
- Real-life applications: Incorporate counting backwards into everyday situations, like countdown to events or calculating change.
- Reverse addition: Practice subtracting small numbers quickly to reinforce backwards thinking.
Implementing these learning strategies can significantly improve students' ability to count backwards:
- Start with smaller numbers and gradually increase complexity.
- Use multisensory approaches, combining visual, auditory, and kinesthetic learning.
- Encourage regular practice through daily warm-up exercises or homework assignments.
- Utilize technology, such as interactive apps or online games, to make learning more engaging.
- Provide immediate feedback and positive reinforcement to boost confidence.
Remember that mastering the skill of counting backwards takes time and patience. Consistent practice and the application of these tips and strategies will help students overcome challenges and develop strong mental math abilities. By addressing common difficulties and providing targeted support, educators and parents can help students build a solid foundation for more advanced mathematical concepts in the future.
Conclusion
In summary, this article has explored the essential skill of counting backwards, highlighting its significance in mathematical development and cognitive growth. We've covered various strategies and techniques to master this skill, from simple counting exercises to more advanced mental math methods. The introduction video provided a crucial foundation for understanding the concept, demonstrating practical applications and common challenges. It's important to recognize that regular practice is key to improving your ability to count backwards efficiently. We encourage readers to incorporate these exercises into their daily routines, whether it's during commutes, idle moments, or dedicated study sessions. By honing this skill, you'll enhance your overall mathematical prowess and problem-solving abilities. For those eager to delve deeper into this topic, we invite you to explore our related resources, join our community forums, or sign up for our newsletter to receive more tips and exercises. Keep counting, and watch your math skills soar!
Introduction to Counting Backwards: How do we count backwards?
Counting backwards is a fundamental skill that is the reverse of counting forwards. It involves starting from a higher number and counting down to a lower number. This skill is useful in various real-life scenarios, such as keeping track of items, managing time, and performing basic arithmetic operations. In this guide, we will explore the concept of counting backwards through a step-by-step approach.
Step 1: Understanding the Concept
To begin with, it's important to understand that counting backwards is simply the reverse of counting forwards. When we count forwards, we start from a lower number and move to a higher number. For example, counting forwards from 1 to 6 would be: 1, 2, 3, 4, 5, 6. In contrast, counting backwards involves starting from the higher number and moving to the lower number. For instance, counting backwards from 6 to 1 would be: 6, 5, 4, 3, 2, 1.
Step 2: Practical Example with Donuts
Let's use a practical example to illustrate counting backwards. Imagine you went to the store and bought six donuts. When you count the donuts forwards, you would say: 1 donut, 2 donuts, 3 donuts, 4 donuts, 5 donuts, and 6 donuts. Now, suppose you get home and some of your friends come over and eat some of the donuts. To find out how many donuts are left, you would count backwards.
Start from the total number of donuts you had, which is 6. As each donut is eaten, you count down: 6, 5, 4, 3, 2, 1. If three donuts are eaten, you would count: 6, 5, 4. This means you have 3 donuts left. Counting backwards helps you keep track of the remaining items.
Step 3: Counting Backwards with Digits
When counting backwards, we use the same digits as we do when counting forwards. The digits we use are: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. When counting forwards, we move from left to right, starting from 0 and going up to 9. For example, counting forwards would be: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
In contrast, when counting backwards, we start from the highest digit and move to the lowest digit. This means we count from 9 down to 0. For example, counting backwards would be: 9, 8, 7, 6, 5, 4, 3, 2, 1, 0. This reverse order helps us understand the concept of decrementing numbers.
Step 4: Applying Counting Backwards in Real Life
Counting backwards is not just a theoretical concept; it has practical applications in everyday life. For instance, when you are cooking and need to keep track of time, you might count down the minutes until your food is ready. Similarly, in sports, countdowns are often used to signal the end of a game or a race.
Another example is in budgeting and finance. When managing expenses, you might start with a total budget and count down as you spend money. This helps you keep track of how much money is left and avoid overspending. Counting backwards is also useful in educational settings, such as teaching children subtraction and understanding the concept of negative numbers.
Step 5: Practice Makes Perfect
Like any other skill, counting backwards improves with practice. Start by practicing with small numbers and gradually increase the range as you become more comfortable. Use everyday situations to practice counting backwards, such as counting down the days until an event, the number of steps you take, or the number of items you have.
Engage in activities that require counting backwards, such as playing games that involve countdowns or solving puzzles that require you to think in reverse order. The more you practice, the more intuitive counting backwards will become.
Conclusion
Counting backwards is a valuable skill that is the reverse of counting forwards. It involves starting from a higher number and counting down to a lower number. By understanding the concept, using practical examples, and practicing regularly, you can master the skill of counting backwards. This skill is useful in various real-life scenarios and can enhance your ability to manage time, track items, and perform arithmetic operations.
FAQs
-
Why is counting backwards important for children?
Counting backwards is crucial for children's mathematical development as it builds number sense, improves memory, and enhances cognitive flexibility. It lays the foundation for subtraction, mental math, and problem-solving skills. This skill also prepares children for more advanced mathematical concepts and helps them gain confidence in manipulating numbers.
-
How can I practice counting backwards with my child?
You can practice counting backwards with your child through various engaging activities:
- Use a number line to visually represent backwards movement
- Play countdown games or use countdown timers for everyday tasks
- Practice skip counting backwards (e.g., by 2s, 5s, or 10s)
- Use objects like toys or snacks to make the process tangible
- Incorporate backwards counting into daily routines, like brushing teeth or getting dressed
-
What are some common challenges when learning to count backwards?
Common challenges include:
- The mental shift required to think in reverse
- Maintaining focus and avoiding errors, especially with larger numbers
- Transitioning between decades or hundreds
- Applying the skill to real-world situations
-
How does counting backwards relate to subtraction?
Counting backwards is closely related to subtraction. When we count backwards, we are essentially performing repeated subtraction by one. This connection helps children understand the concept of subtraction more intuitively. For example, counting backwards from 10 to 7 is equivalent to subtracting 3 from 10 (10 - 3 = 7). This relationship forms the basis for more complex subtraction operations and mental math skills.
-
At what age should children start learning to count backwards?
Children typically start learning to count backwards around age 5 or 6, usually in kindergarten or first grade. However, this can vary based on individual development and prior exposure to numbers. It's important to introduce the concept gradually, starting with small numbers (e.g., 10 to 0) and progressing to larger numbers as the child becomes more comfortable. Remember that every child develops at their own pace, so it's essential to provide support and encouragement throughout the learning process.
Prerequisite Topics for Counting Backwards
Understanding the concept of counting backwards is crucial in mathematics, but it's essential to grasp certain foundational topics first. Two key prerequisites that significantly contribute to mastering this skill are place value and the negative exponent rule.
Let's start with place value. This fundamental concept is vital when counting backwards, especially when dealing with multi-digit numbers. When we count backwards, we often need to borrow across place values. For instance, when counting back from 100, we need to understand how the digits in each place value change. As we move from 100 to 99, the hundreds place remains the same, but the tens and ones places change. This understanding of place value is crucial for accurately counting backwards, particularly with larger numbers.
The concept of negative numbers on a number line is another essential prerequisite for counting backwards. While it might seem more advanced, understanding negative numbers helps students grasp the idea that counting backwards can extend beyond zero. This knowledge is particularly useful when dealing with temperature, debt, or other real-world scenarios where negative numbers are common. The negative exponent rule, while more advanced, builds on this understanding and helps students see numbers as part of a continuous spectrum, rather than stopping at zero.
When students have a solid grasp of place value, they can more easily visualize how numbers change as they count backwards. This visualization is crucial for mental math and estimation skills. Similarly, understanding negative numbers allows students to continue counting backwards confidently, even when they reach zero, opening up a whole new realm of mathematical possibilities.
Moreover, these prerequisite topics don't just aid in counting backwards; they form the foundation for more advanced mathematical concepts. Place value is essential for understanding decimals, percentages, and even algebra. The concept of negative numbers is crucial for algebraic operations, graphing, and solving equations.
By mastering these prerequisites, students not only become proficient in counting backwards but also develop a deeper understanding of number systems and mathematical relationships. This comprehensive understanding helps in problem-solving across various mathematical domains and real-world applications.
In conclusion, while counting backwards might seem like a simple skill, it relies on a solid understanding of more fundamental concepts. By ensuring a strong grasp of place value and negative numbers, students can approach counting backwards with confidence and extend this skill to more complex mathematical operations. These prerequisites serve as building blocks, not just for counting backwards, but for a wide range of mathematical concepts that students will encounter in their future studies.

