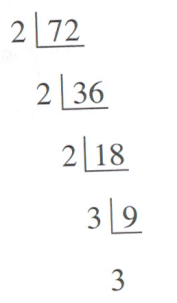Factorización prima
Notas del Tema
Un número primo es un número natural que puede dividirse solamente entre el uno o él mismo y obtener otro número entero como resultado.
Los números compuestos son aquellos números enteros que no son primos, por lo tanto, tienen más de dos factores. La factorización prima es un proceso que implica encontrar los factores primos de un número.
Factor:
Recuerda que cuando haces una multiplicación, a los números que se multiplican se les llaman factores; por esta razón, a un par de números que se multiplican y producen un tercero se les llaman los factores del tercer número.
Por ejemplo:
1 × 8 = 8 y 2 × 4 = 8, entonces, los factores de 8 son: 1, 2, 4, 8.
Divisor:
Cualquier número entero que puede dividir exactamente a otro se le llama divisor de este último. Entonces, los divisores de 8 son: 1, 2, 4, 8.
Como te puedes dar cuenta, los factores de un número son iguales a sus divisores.
Números primos:
Los números primos son aquellos que sólo tienen dos divisores (también se puede decir que son aquellos que sólo tienen dos factores) el uno y ellos mismos.
Ejemplo: 2, 3, 5, 7, 11, 13, 17
Números compuestos:
Cualquier número entero que no es primo (tiene más de dos divisores o dos factores).
Ejemplo: 4, 6, 8, 9, 10, 12, 14, 15, 16
El cero y el uno no son números primos o compuestos.
Al uno puede llamársele como ¨la unidad¨.
Árbol de factores:
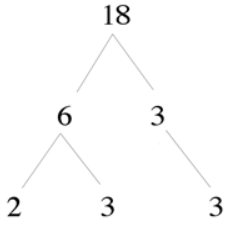
Es un método utilizado para encontrar los factores primos de un número usando un diagrama de árbol. Usando este método, se selecciona un par de factores del número en cuestión y se identifica si alguno de ellos es primo. Si no lo es, cada factor es descompuesto en sus propios factores y se vuelve a revisar si alguno de ellos es primo. El proceso se repite hasta que el número se ha descompuesto en todos sus factores y se han encontrado todos los factores primos. Ejemplo: Los factores primos de 18 son: 2 × 3 × 3 = 18.
Árbol de factores
División sucesiva:
Este método para encontrar los factores primos de un número utiliza divisiones continuas (una tras otra) entre el menor número primo posible cada vez.
Ejemplo: los factores primos de 72 son: 2 × 2 × 2 × 3 × 3 = 72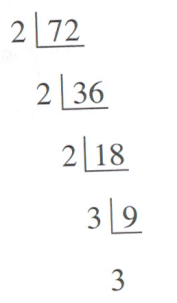
Los números compuestos son aquellos números enteros que no son primos, por lo tanto, tienen más de dos factores. La factorización prima es un proceso que implica encontrar los factores primos de un número.
Factor:
Recuerda que cuando haces una multiplicación, a los números que se multiplican se les llaman factores; por esta razón, a un par de números que se multiplican y producen un tercero se les llaman los factores del tercer número.
Por ejemplo:
1 × 8 = 8 y 2 × 4 = 8, entonces, los factores de 8 son: 1, 2, 4, 8.
Divisor:
Cualquier número entero que puede dividir exactamente a otro se le llama divisor de este último. Entonces, los divisores de 8 son: 1, 2, 4, 8.
Como te puedes dar cuenta, los factores de un número son iguales a sus divisores.
Números primos:
Los números primos son aquellos que sólo tienen dos divisores (también se puede decir que son aquellos que sólo tienen dos factores) el uno y ellos mismos.
Ejemplo: 2, 3, 5, 7, 11, 13, 17
Números compuestos:
Cualquier número entero que no es primo (tiene más de dos divisores o dos factores).
Ejemplo: 4, 6, 8, 9, 10, 12, 14, 15, 16
El cero y el uno no son números primos o compuestos.
Al uno puede llamársele como ¨la unidad¨.
Árbol de factores:
Es un método utilizado para encontrar los factores primos de un número usando un diagrama de árbol. Usando este método, se selecciona un par de factores del número en cuestión y se identifica si alguno de ellos es primo. Si no lo es, cada factor es descompuesto en sus propios factores y se vuelve a revisar si alguno de ellos es primo. El proceso se repite hasta que el número se ha descompuesto en todos sus factores y se han encontrado todos los factores primos. Ejemplo: Los factores primos de 18 son: 2 × 3 × 3 = 18.

División sucesiva:
Este método para encontrar los factores primos de un número utiliza divisiones continuas (una tras otra) entre el menor número primo posible cada vez.
Ejemplo: los factores primos de 72 son: 2 × 2 × 2 × 3 × 3 = 72