Subtraction strategies
Topic Notes
In this lesson, we will learn:
- The subtraction strategy of: (1) using a friendly number with adjustment, (2) adding to both numbers to create a friendly number, and (3) counting on from the first number (subtrahend)
- Understanding subtracting by 9
Notes:
- Method 1: change into a "friendly" number then adjust (by adding)
- Round one the number being taken away to the nearest multiple of 10
- Then adjust by adding how much you rounded by to get the answer
- Method 2: make "friendly" numbers by adding to both numbers
- Add to one of the numbers so that it becomes the nearest multiple of 10
- Add the same amount to the other number
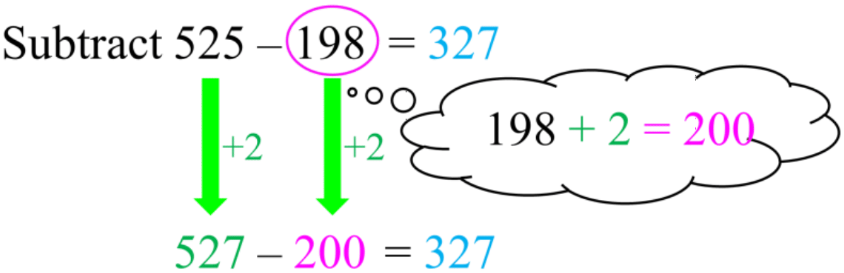
- Method 3: subtracting by counting on
- Start with the number you're taking away (the second number)
- Then count up until you get the first number

Introduction to Subtraction Strategies
Subtraction strategies are essential tools for enhancing mental math skills and solving problems efficiently. Our introduction video serves as a crucial starting point, providing a comprehensive overview of these techniques. By watching this video, students gain a solid foundation for understanding and applying various subtraction methods. We focus on three main strategies that prove invaluable in mental math calculations. First, using friendly numbers with adjustment allows for easier computations by rounding to simpler numbers. Second, adding to both numbers maintains the difference while simplifying the problem. Lastly, counting on is a versatile technique for finding the difference between two numbers. These strategies not only improve calculation speed but also deepen mathematical understanding. By mastering these subtraction techniques, students develop stronger problem-solving skills and gain confidence in their mathematical abilities. The introduction video and subsequent practice with these strategies pave the way for more advanced mathematical concepts and applications.
Using Friendly Numbers with Adjustment
Friendly numbers, also known as multiples of 10, play a crucial role in simplifying mental calculations, especially when it comes to subtraction. These numbers are called "friendly" because they are easy to work with in our minds, making arithmetic operations more manageable. In this section, we'll explore how friendly numbers can be used to make subtraction easier through a process of rounding and adjustment.
Friendly numbers are essentially multiples of 10, such as 10, 20, 30, 40, and so on. These numbers are easier to manipulate mentally because they align with our base-10 number system. When we encounter a subtraction problem with numbers that aren't as "friendly," we can use a strategy that involves rounding the subtrahend (the number being subtracted) to the nearest friendly number and then adjusting the result.
Here's how the process works:
- Identify the subtraction problem.
- Round the subtrahend to the nearest friendly number (multiple of 10).
- Perform the subtraction using the rounded number.
- Adjust the result by adding or subtracting the difference between the original subtrahend and the rounded number.
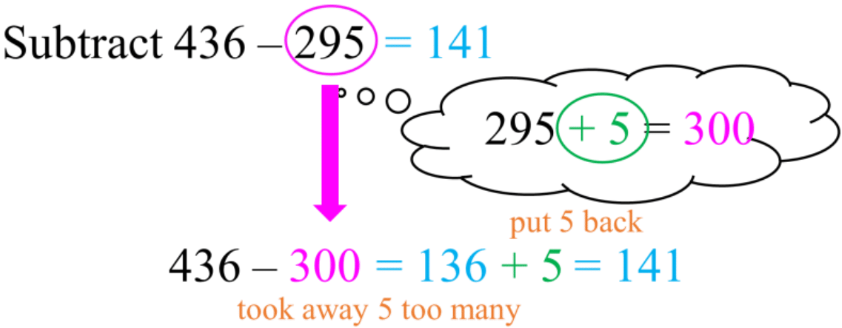
Let's look at an example to illustrate this method. Consider the subtraction problem: 436 - 295
- Our problem is 436 - 295.
- We round 295 up to the nearest friendly number, which is 300.
- Now we calculate 436 - 300 = 136.
- Since we rounded up by 5 (300 - 295 = 5), we need to add 5 back to our result: 136 + 5 = 141.
Therefore, 436 - 295 = 141.
This strategy simplifies mental calculations by breaking down the problem into more manageable steps. Instead of trying to subtract 295 from 436 in one go, we work with the friendly number 300 and then make a small adjustment. This approach is particularly useful when dealing with numbers that end in digits close to 0 or 5.
Here's another example: 724 - 398
- We start with 724 - 398.
- Round 398 up to 400.
- Calculate 724 - 400 = 324.
- Since we rounded up by 2, we add 2 back: 324 + 2 = 326.
The result is 724 - 398 = 326.
This method of using friendly numbers with adjustment is particularly beneficial for mental math and quick estimations. It allows us to work with easier numbers in our heads, reducing the cognitive load and potential for errors. By rounding to multiples of 10, we leverage our familiarity with these friendly numbers to perform calculations more efficiently.
The key to mastering this technique is practice. As you become more comfortable with identifying friendly numbers and making quick adjustments, you'll find that your mental math skills improve significantly. This strategy is not only useful for subtraction but can also be adapted for addition, multiplication, and division problems.
In conclusion, the concept of friendly numbers and the rounding with adjustment method provide a powerful tool for simplifying mental subtraction. By breaking down complex problems into more manageable steps involving multiples of 10, we can perform calculations more quickly and accurately in our heads. This approach enhances our overall numeracy skills and builds confidence in tackling mathematical problems without relying on calculators or written methods.
Adding to Both Numbers for Easier Subtraction
Subtraction can often be challenging, especially when dealing with numbers that aren't "friendly" to work with mentally. One effective strategy to simplify subtraction is adding to both numbers to create a friendly number. This method, known as "adding to both numbers," can significantly enhance your mental math skills and make calculations more manageable.
The principle behind this strategy is based on the fundamental rule of subtraction: if we add the same amount to both numbers in a subtraction problem, the difference between them remains unchanged. This concept can be easily visualized using a number line.
Imagine a number line with two points representing the minuend and subtrahend. When we add the same amount to both numbers, we're essentially shifting both points to the right on the number line by the same distance. The gap between these points - which represents the difference - remains constant, regardless of where we move them on the line.
Let's walk through a step-by-step example to illustrate this process. Consider the subtraction problem: 525 - 198
Step 1: Identify the subtrahend (198) and determine how much needs to be added to make it a friendly number. In this case, adding 2 would make it 200, which is much easier to work with.
Step 2: Add the same amount (2) to both numbers: 525 + 2 = 527 198 + 2 = 200
Step 3: Rewrite the problem with the new numbers: 527 - 200
Step 4: Solve the new, friendlier subtraction problem: 527 - 200 = 327
The answer, 327, is the same as if we had solved 525 - 198 directly, but the mental calculation is much simpler.
This method works particularly well when the subtrahend is close to a round number. For instance, in problems like 632 - 298 or 1045 - 999, adding 2 or 1 respectively to both numbers can significantly simplify the calculation.
The "adding to both numbers" strategy offers several benefits for mental math: 1. It transforms difficult numbers into friendlier ones, making mental calculations more approachable. 2. It reduces the likelihood of errors in borrowing or regrouping, which are common in traditional subtraction methods. 3. It encourages flexible thinking about numbers and their relationships. 4. It can be faster than traditional column subtraction for those proficient in mental math.
To further illustrate the power of this method, let's consider another example: 743 - 496
In this case, we can add 4 to both numbers: 743 + 4 = 747 496 + 4 = 500 The problem becomes 747 - 500, which is much easier to solve mentally. The answer is 247, which is the same as the original problem.
When using a number line to visualize this process, imagine starting at 743 and moving left by 496 units. This is equivalent to moving right by 4 units (to 747), then left by 500 units. The end point remains the same, illustrating why the difference is unchanged.
While this method is powerful, it's important to note that it may not always be the best approach for every subtraction problem. The key is to recognize when it's most useful - typically when the subtrahend is close to a round number or when the numbers involved make mental calculation challenging.
In conclusion, the strategy of adding the same amount to both the minuend and subtrahend to create a friendly number is a valuable tool in your mental math arsenal. By transforming difficult problems into more manageable ones, this method can significantly enhance your ability to perform quick, accurate calculations in your head. Practice with various examples to become proficient in identifying when and how to apply this technique effectively.
Counting On: A Reverse Approach to Subtraction
The counting on method is an innovative and intuitive approach to finding the difference between two numbers in subtraction. This technique offers a fresh perspective on mental subtraction, particularly beneficial for visual learners and those who find traditional subtraction methods challenging. By utilizing place values and a step-by-step counting process, this method transforms subtraction into a more accessible and engaging mathematical operation.
At its core, the counting on method involves starting from the subtrahend (the number being subtracted) and counting up to the minuend (the number you're subtracting from). This reverse approach allows learners to visualize the difference between the two numbers more clearly. The process relies heavily on understanding place values, specifically working with hundreds, tens, and ones.
Let's explore this method using the example of 367 - 150. In traditional subtraction, we would start with 367 and take away 150. However, with the counting on method, we begin at 150 and count our way up to 367, keeping track of how much we've added along the way.
Here's how it works step-by-step:
- Start at 150 (the subtrahend).
- Count up to the nearest hundred: 150 to 200 (added 50).
- Count up to 300 (added another 100).
- Finally, count up to 367 (added 67 more).
By adding these increments together (50 + 100 + 67), we arrive at the difference of 217. This method allows learners to work with more manageable numbers and visualize the process of bridging between the subtrahend and minuend.
The counting on method is particularly effective because it leverages our natural inclination to count forward rather than backward. It also reinforces place value concepts, as learners consciously work with hundreds, tens, and ones throughout the process. This approach can be especially helpful for those who struggle with borrowing or regrouping in traditional subtraction.
One of the key advantages of this method is its flexibility. Learners can adjust their counting strategy based on their comfort level with different number ranges. For instance, some might prefer to count by tens, while others might find it easier to jump to the nearest hundred first.
The counting on method also serves as an excellent tool for developing mental math skills. As learners become more proficient, they can perform larger jumps in their head, eventually leading to quicker mental calculations. This skill is invaluable in real-world scenarios where quick estimations and mental math are often required.
Moreover, this approach aligns well with the concept of number lines, providing a visual representation of the subtraction process. Teachers and parents can use number lines as a complementary tool to illustrate the counting on method, further enhancing understanding and retention.
While the counting on method is highly effective, it's important to note that it should be taught alongside traditional subtraction techniques. Having a diverse toolkit of mathematical strategies allows learners to choose the most appropriate method for different situations and problem types.
In conclusion, the counting on method offers a fresh, intuitive approach to subtraction that can significantly benefit many learners. By transforming subtraction into a process of counting up and utilizing place values, this method makes the concept more accessible and less intimidating. As with any mathematical technique, practice and consistent application will lead to improved speed and accuracy. Embracing diverse methods like counting on not only enhances mathematical skills but also fosters a more positive and confident attitude towards mathematics as a whole.
Comparing and Contrasting Subtraction Strategies
When it comes to mental math and problem-solving, having a variety of subtraction strategies at your disposal can greatly enhance your efficiency and accuracy. In this section, we'll compare the three subtraction strategies we've discussed, highlighting their strengths and identifying situations where each might be most useful. By understanding these strategies and practicing them, you'll be better equipped to tackle a wide range of mathematical challenges.
The first strategy we explored was the "counting up" method. This approach is particularly useful when dealing with numbers that are close together or when the difference between them is small. For example, when subtracting 98 from 103, counting up from 98 to 103 (98, 99, 100, 101, 102, 103) quickly reveals the difference of 5. The strength of this method lies in its intuitive nature and its ability to visualize the gap between numbers. It's especially effective for mental calculations and can be a go-to strategy for quick estimations in everyday situations.
Our second strategy, "breaking apart numbers," involves decomposing numbers into more manageable parts. This method shines when working with larger numbers or when precision is required. For instance, when subtracting 268 from 735, we can break it down as follows: 735 - 200 = 535, 535 - 60 = 475, 475 - 8 = 467. The strength of this approach is its flexibility and how it aligns with our understanding of place value. It's particularly useful in written calculations and can be adapted to suit various problem types.
The third strategy we discussed was "finding a friendly number." This method involves adjusting one or both numbers to create an easier calculation, then compensating for the adjustment. It's especially powerful when dealing with numbers that are close to multiples of 10 or 100. For example, when subtracting 98 from 256, we can adjust 98 to 100, subtract (256 - 100 = 156), then add back the 2 we subtracted extra (156 + 2 = 158). The strength of this method lies in its ability to simplify complex calculations by leveraging our comfort with round numbers.
When comparing these strategies, it's important to consider the specific problem at hand. For close numbers or small differences, the counting up method often proves most efficient. In a problem like 502 - 498, counting up from 498 to 502 (4 steps) is likely faster than breaking apart the numbers or finding a friendly number.
For larger numbers or when working with pen and paper, the breaking apart strategy can be incredibly useful. It allows for a systematic approach that minimizes errors. Consider a problem like 8,742 - 3,569. Breaking this down into manageable parts (8,000 - 3,000, 700 - 500, 40 - 60, 2 - 9) allows for a step-by-step solution that's less prone to mistakes.
The friendly number strategy often shines with numbers ending in 8 or 9. For instance, in a problem like 1,000 - 399, adjusting 399 to 400 and then subtracting from 1,000 (giving 600) before adding back 1 is likely more efficient than breaking apart or counting up.
It's crucial to remember that the effectiveness of each strategy can vary depending on the individual and the specific problem. What works best for one person might not be the most efficient method for another. That's why it's essential to practice all three strategies regularly. By doing so, you'll develop a intuitive sense of which method to apply in different situations.
To enhance your skills, try solving a variety of subtraction problems using each method. Start with simple calculations and gradually increase the complexity. Pay attention to which strategy feels most natural and produces the quickest results for different types of problems. Over time, you'll likely find that you gravitate towards certain methods for specific problem types.
Remember, the goal is not to rigidly adhere to one strategy but to build a flexible problem-solving toolkit. By mastering these three subtraction strategies, you'll improve your mental math efficiency and overall mathematical confidence. Whether you're calculating a tip, balancing a budget, or solving complex equations, having these strategies at your
Practice Exercises and Real-World Applications
To master subtraction strategies and enhance your mental math skills, regular practice is essential. Let's explore some practice problems and real-world applications for each subtraction technique.
1. Counting Up Strategy
Practice: Calculate 100 - 67
Real-world scenario: You have a $100 bill and spend $67. How much change should you receive?
2. Breaking Down Numbers
Practice: Solve 324 - 168
Real-world scenario: Your monthly budget is $324, and you've already spent $168. How much do you have left?
3. Compensation Method
Practice: Calculate 1000 - 399
Real-world scenario: A store offers a product for $1000, with a discount of $399. What's the final price?
4. Using Complements
Practice: Solve 50 - 27
Real-world scenario: You need 50 items for an event, but only have 27. How many more do you need to buy?
5. Rounding and Adjusting
Practice: Calculate 785 - 497
Real-world scenario: Your bank account has $785, and you want to make a purchase of $497. How much will remain?
Tips for Improving Mental Math Skills
- Practice daily: Set aside 10-15 minutes each day for mental math exercises.
- Start simple: Begin with easier problems and gradually increase difficulty.
- Use real-life situations: Apply mental math in everyday scenarios like shopping or budgeting.
- Play math games: Engage in number-based games to make practice enjoyable.
- Visualize numbers: Create mental images of numbers to aid calculations.
- Learn number relationships: Understand how numbers relate to each other (e.g., multiples, factors).
- Embrace mistakes: Use errors as learning opportunities to improve your skills.
By consistently practicing these subtraction strategies and applying them to real-world situations, you'll significantly enhance your mental math abilities. Remember, mental math is a skill that improves with regular use. Whether you're calculating change, estimating discounts, or managing your budget, these techniques will prove invaluable in your daily life. Challenge yourself to use mental math in various scenarios, and you'll soon find that complex calculations become second nature. With dedication and practice, you'll develop a mathematical agility that will serve you well in both personal and professional contexts.
Conclusion: Mastering Subtraction Strategies
In this guide, we've explored three powerful subtraction strategies: counting up, breaking apart numbers, and using friendly numbers. The introduction video laid the foundation for understanding these concepts, demonstrating their practical applications in mental math. By mastering these techniques, you can significantly enhance your subtraction skills and overall mathematical prowess. Remember, consistent practice is key to improving your mental math abilities. We encourage you to continue honing these methods in your daily calculations. As you gain confidence, challenge yourself with more complex subtraction problems to further solidify your skills. Don't stop here explore other mental math techniques to broaden your mathematical toolkit. By incorporating these strategies into your routine, you'll soon find yourself performing calculations with greater speed and accuracy. Ready to take your subtraction mastery to the next level? Try tackling some advanced problems now and experience the difference these methods can make in your mental math journey!
Example:
Subtracting by 9 strategy
Subtract 9 by: subtracting 10 first, then putting 1 back
17 - 9 = ____
17 - 10 = ____ + 1 = ____
Step 1: Understand the Strategy
For this question, we are working with the subtraction strategy specifically designed for subtracting by 9. The strategy involves two main steps: first, subtracting 10 from the original number, and then adding 1 back to the result. This method simplifies the subtraction process by breaking it down into more manageable parts.
Step 2: Subtract 10 from the Original Number
Start by subtracting 10 from the original number. In this case, the original number is 17. Subtracting 10 from 17 is straightforward:
17 - 10 = 7
This step simplifies the subtraction by dealing with a round number, making it easier to handle mentally.
Step 3: Add 1 Back to the Result
After subtracting 10, you need to add 1 back to the result. This is because subtracting 10 removes one more than needed when subtracting 9. Therefore, you need to correct this by adding 1 back:
7 + 1 = 8
This step ensures that the final result accurately reflects the subtraction of 9 from the original number.
Step 4: Verify the Result
To ensure the accuracy of your result, you can verify it by adding 9 back to the final answer. If the sum equals the original number, your subtraction is correct:
8 + 9 = 17
This verification step confirms that the subtraction strategy was applied correctly and that the final result is accurate.
Step 5: Summarize the Process
In summary, the subtracting by 9 strategy involves two main steps: subtracting 10 from the original number and then adding 1 back to the result. This method simplifies the subtraction process and ensures accuracy. By following these steps, you can easily subtract 9 from any number:
17 - 9 = 8
17 - 10 = 7 + 1 = 8
This strategy can be applied to other numbers as well, making it a useful tool for quick and accurate subtraction.
FAQs
-
What are the three main subtraction strategies discussed in the introduction video?
The three main subtraction strategies introduced are: using friendly numbers with adjustment, adding to both numbers, and counting on. These strategies are designed to enhance mental math skills and make subtraction more efficient and manageable.
-
How does the "using friendly numbers with adjustment" strategy work?
This strategy involves rounding the subtrahend (the number being subtracted) to the nearest multiple of 10, performing the subtraction, and then adjusting the result. For example, in 436 - 295, you would round 295 to 300, subtract 300 from 436 to get 136, and then add back 5 to get the final answer of 141.
-
What is the benefit of the "adding to both numbers" strategy?
This strategy simplifies subtraction by adding the same amount to both the minuend and subtrahend, creating easier numbers to work with mentally. It's particularly useful when the subtrahend is close to a round number. For instance, 525 - 198 can be transformed into 527 - 200, which is easier to calculate mentally.
-
How does the "counting on" method differ from traditional subtraction?
The counting on method is a reverse approach where you start from the subtrahend and count up to the minuend, keeping track of the difference. This method is especially helpful for visual learners and those who find traditional subtraction challenging. It utilizes place values and can be visualized using a number line.
-
How can I improve my mental math skills using these subtraction strategies?
To improve your mental math skills, practice these strategies regularly with various problems. Start with simpler calculations and gradually increase complexity. Apply these methods in real-life situations like shopping or budgeting. Consistent practice and application in everyday scenarios will help you develop mathematical agility and confidence in performing mental calculations.
Prerequisite Topics
Understanding the foundation of mathematics is crucial for mastering more advanced concepts. When it comes to learning subtraction strategies, having a solid grasp of prerequisite topics is essential. One of the most fundamental prerequisites for subtraction strategies is place value understanding. This concept forms the bedrock of numerical operations and is vital for developing effective subtraction techniques.
Place value is the cornerstone of our number system, determining the value of each digit based on its position within a number. When students have a strong comprehension of place value, they can approach subtraction with greater confidence and accuracy. This understanding allows them to break down numbers into their component parts, making it easier to perform mental calculations and apply various subtraction strategies.
For instance, when subtracting larger numbers, students often need to regroup or borrow from adjacent columns. This process relies heavily on a solid place value understanding. Without this foundation, students may struggle to comprehend why they're moving digits from one column to another, leading to confusion and errors in their calculations.
Moreover, many subtraction strategies, such as counting up or using number lines, require students to recognize the relative values of numbers. This skill is directly tied to place value knowledge. When students can quickly identify that 80 is ten less than 90, or that 305 is five more than 300, they can employ these insights to subtract more efficiently.
The importance of place value extends beyond just subtraction. It's a concept that underpins all arithmetic operations, including addition, multiplication, and division. By investing time in mastering place value, students are not only preparing themselves for subtraction strategies but also laying the groundwork for future mathematical success.
As students progress to more complex subtraction problems, such as those involving decimals or larger numbers, their reliance on place value understanding intensifies. The ability to align digits correctly and manipulate numbers based on their place value becomes even more critical. This skill allows students to tackle problems with confidence and avoid common pitfalls associated with misaligned digits or misunderstood number magnitudes.
In conclusion, the journey to mastering subtraction strategies begins with a solid foundation in place value. By ensuring students have a firm grasp of this prerequisite topic, educators and learners alike can pave the way for smoother learning experiences and more effective application of various subtraction techniques. As students continue to build upon this knowledge, they'll find themselves better equipped to handle increasingly complex mathematical challenges, not just in subtraction, but across all areas of arithmetic.

