Calculating and Estimating Area and Perimeter
Topic Notes
In this lesson, we will learn:
- How to count areas with squares and/or triangles (unit squares and half unit squares)
- How to estimate areas of shapes on an area grid
Notes:
- Review: finding perimeter and area for rectangular figures

- How do you find the area of shapes that are not made of squares?
- If you cut a square diagonally, you will get a triangle (half a square is a triangle)

- If you cut 2 squares diagonally (2 cm2), you will get half the area (1 cm2)
- There are other variations of getting half of a square (1/2 cm2 or 0.5 cm2)
- There will also be cases where you won't know the exact amount shaded in one square, but you can say whether it is more or less than half
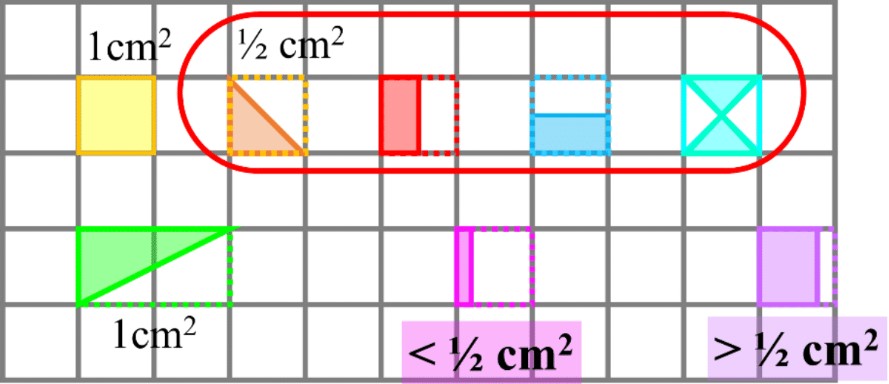
- To estimate areas of a shape on a grid, we can get close to the actual area by:
- Counting all the whole unit squares (fully shaded in or covered by the shape)
- Counting all the half unit squares (most commonly the diagonal triangle)
- Rounding any squares shaded more than half up to 1 cm2
- Rounding any squares shaded less than half down to 0 cm2
Introduction
Welcome to the fascinating world of calculating and estimating area and perimeter! This essential mathematical concept is crucial for understanding shapes and spaces in our everyday lives. Our introduction video serves as a gateway to this topic, providing a clear and engaging overview that sets the foundation for your learning journey. As you progress, you'll discover how to count areas using squares and triangles, mastering the art of breaking complex shapes into manageable units. One of the key skills you'll develop is estimating areas on a grid, a technique that combines visual perception with mathematical reasoning. By working with unit squares and grids, you'll gain a practical understanding of area measurement. This knowledge not only enhances your mathematical abilities but also has real-world applications in fields like architecture, landscaping, and design. Get ready to explore the dimensions of shapes and spaces!
Review of Perimeter and Area for Rectangular Figures
Understanding the concepts of perimeter and area is crucial when working with rectangular figures. These two measurements provide different information about the shape and size of a rectangle, and it's important to distinguish between them. Let's explore these concepts using the example from the video to clarify their meanings and calculations.
Perimeter refers to the distance around the outside of a shape. For a rectangle, you can calculate the perimeter by tracing along its outer edges. In the video example, we saw a rectangular figure on a grid. To find the perimeter, we simply add up the lengths of all four sides. Remember, perimeter is measured in linear units, such as inches, centimeters, or feet.
Area, on the other hand, represents the space inside a shape. For rectangles, we calculate area by determining how many unit squares fit within the figure. In our grid example, each small square represents one unit of area. To find the total area, we count all the unit squares that make up the rectangle. Area is expressed in square units, like square inches or square centimeters.
The key difference between perimeter and area lies in what they measure. Perimeter focuses on the boundary of the shape, while area considers the entire surface within that boundary. Think of perimeter as the fence around a field, and area as the space inside that fence.
Let's apply these concepts to our grid example. To calculate the perimeter, we count the number of unit lengths along each side and add them together. For the area, we count the total number of grid squares within the rectangle. This method of using unit squares or grid squares is an excellent visual way to understand area in square units, especially for younger learners or those new to the concept.
It's important to note that while perimeter and area are related to the same shape, they don't always change proportionally. A rectangle with a large perimeter doesn't necessarily have a large area, and vice versa. For instance, a long, narrow rectangle might have a greater perimeter but a smaller area compared to a more square-like rectangle with the same perimeter.
Understanding these concepts is fundamental in various real-world applications of perimeter and area, from calculating the amount of fencing needed for a garden (perimeter) to determining the amount of carpet required for a room (area). By mastering perimeter and area calculations for rectangular figures, you'll build a strong foundation for more advanced geometric concepts and problem-solving skills.
Calculating Area with Triangles
When calculating area, shapes that include triangles require a special approach. Understanding that a triangle is essentially half a square is key to mastering this concept. This insight allows us to accurately measure and estimate areas of complex shapes by breaking them down into more manageable components.
To begin, let's consider a unit square. When divided diagonally, this square forms two equal triangles. Each of these triangles represents half a unit square, a fundamental concept in area calculation. This relationship between squares and triangles is crucial for solving more complex shapes area problems.
There are various ways to represent half a unit square: 1. A right-angled triangle with legs of 1 unit each 2. An isosceles triangle with a base of 1 unit and a height of 1 unit 3. Any triangle that fits exactly into half of a unit square
When faced with shapes that include triangles, the strategy is to count these triangles as half squares. For instance, if you encounter a shape with 3 full squares and 2 triangles, you would calculate the area as 3 + (2 × 0.5) = 4 square units. This method allows for precise area calculations of irregular shapes.
In practical applications, such as estimating the area of a lake on a map, you might encounter partial squares along the edges. These can often be approximated as triangles. By counting full squares and then adding half a unit for each triangle, you can arrive at a reasonably accurate estimation of the total area.
It's important to note that not all triangles in a shape will be exactly half a square. In such cases, estimation skills come into play. You may need to visually assess whether a triangle is slightly larger or smaller than half a square and adjust your calculations accordingly.
For more complex shapes, it can be helpful to overlay a grid of unit squares. This allows you to easily identify full squares and triangular sections. Remember, two triangles that form a square count as one full unit of area.
Practice is key to mastering this technique. Start with simple shapes and gradually move to more complex ones. You'll find that breaking down areas into squares and triangles becomes more intuitive over time, enabling you to quickly and accurately estimate areas of various shapes.
In summary, calculating area with triangles involves recognizing them as half squares, counting full squares, and adding half units for triangular sections. This method, combined with careful estimation when needed, provides a powerful tool for area calculation in both academic and real-world scenarios.
Estimating Area on a Grid
Estimating area on a grid is a valuable skill for calculating the size of irregular shapes. This process involves using a grid overlay to approximate the area of a shape that doesn't conform to standard geometric formulas. The method is particularly useful in fields such as geography, biology, and engineering, where precise measurements of irregular shapes or regions are often required.
To begin the estimation process, place the irregular shape on a grid where each square represents a known unit of area. The grid acts as a reference point, allowing you to count the number of squares covered by the shape. However, not all squares will be completely filled, which is where the estimation comes into play.
When dealing with partially filled squares, follow these guidelines:
- Count squares that are more than half filled as whole squares.
- Disregard squares that are less than half filled.
- For squares that are approximately half filled, use your judgment to decide whether to include them or not.
This approach helps balance out the overestimation of some squares with the underestimation of others, leading to a more accurate overall estimate.
The rounding process is crucial in this estimation technique. As you count the squares, keep a running total of whole squares and partial squares. Once you've covered the entire shape, round your final count to the nearest whole number. This rounding step is essential because it acknowledges the inherent imprecision in estimating irregular shapes while still providing a useful approximation.
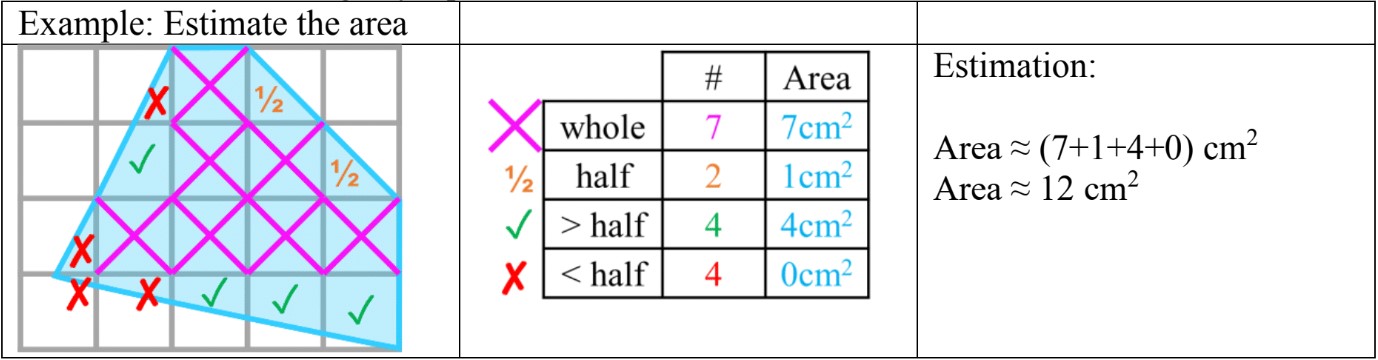
Let's walk through an example to demonstrate this process step-by-step:
- Place the irregular shape on a grid where each square represents 1 square unit.
- Start at one edge of the shape and begin counting whole squares. Let's say we count 15 whole squares.
- Next, count squares that are more than half filled. We find 7 such squares.
- Now, look at squares that are approximately half filled. We decide to count 3 of these.
- Add these numbers together: 15 + 7 + 3 = 25 squares.
- Round this number to the nearest whole number, which in this case remains 25.
- Our final estimate for the area of the irregular shape is 25 square units.
This method provides a reasonable estimate of the area, considering the limitations of working with an irregular shape. It's important to note that the accuracy of this estimation improves with a finer grid resolution. A grid with smaller squares will allow for more precise counting and less ambiguity in partially filled squares.
When applying this technique, consistency is key. Establish clear criteria for what constitutes "more than half filled" and stick to it throughout your estimation. This consistency helps minimize errors and ensures that your estimation process is as accurate as possible given the constraints of the method.
In practical applications, this grid estimation technique can be used for various purposes. For instance, geographers might use it to estimate the area of lakes or forest patches on maps. Biologists could apply it to measure leaf surface area or the size of cell clusters under a microscope. Engineers might use it to approximate the cross-sectional area of complex mechanical parts.
While this method is not as precise as advanced computational techniques or direct measurement, it offers a quick and accessible way to estimate areas of irregular shapes. Its simplicity makes it a valuable tool in situations where rough estimates are sufficient or where more sophisticated measurement tools are not available.
In conclusion, estimating area on a grid is a practical skill that combines simple counting with thoughtful estimation. By following the guidelines for handling partially filled squares, applying consistent rounding practices, and working systematically through the shape, you can arrive at a reasonable approximation of an irregular area. This technique bridges the gap between precise geometric calculations and the complex realities of natural and man-made shapes, providing a useful method for area estimation across various fields of study and practical applications.
Practical Application of Area Estimation
Area estimation is a valuable skill that finds numerous applications in real-life situations, offering quick solutions when precise measurements are impractical or unnecessary. This problem-solving technique is used across various fields, from everyday tasks to professional endeavors. Understanding when and how to apply area estimation can significantly enhance efficiency and decision-making processes.
One common practical application of area estimation is in home improvement projects. When planning to paint a room, homeowners often estimate the wall area to determine how much paint to purchase. This quick calculation helps avoid buying excess materials or making multiple trips to the store. Similarly, landscapers use area estimation to approximate the amount of grass seed or mulch needed for a garden, saving time and resources in the planning phase.
In agriculture, farmers frequently employ area estimation techniques to assess crop yields or plan irrigation systems. By estimating field sizes, they can make informed decisions about resource allocation without the need for precise surveying. This approach is particularly useful for large-scale operations where exact measurements would be time-consuming and costly.
Real estate professionals also rely on area estimation when providing initial property valuations. By quickly assessing the approximate size of a house or land parcel, they can offer ballpark figures to clients before conducting detailed measurements. This helps streamline the property evaluation process and provides valuable insights for both buyers and sellers.
In urban planning and development, area estimation plays a crucial role in the early stages of project conceptualization. Planners use this technique to roughly determine the space available for parks, roads, or buildings, allowing for preliminary discussions and feasibility studies without the need for extensive surveys.
Estimation is particularly useful when exact calculations are either impossible or impractical. For instance, in environmental studies, scientists may estimate the area of a forest or wetland using satellite imagery or aerial photographs. This approach provides valuable data for conservation efforts without the need for time-consuming ground surveys.
The key advantage of estimation lies in its ability to provide quick, reasonably accurate results that are sufficient for many decision-making processes. It allows for rapid problem-solving and helps in situations where time or resources are limited. However, it's important to recognize when estimation is appropriate and when more precise measurements are necessary.
To improve accuracy in estimation, several tips can be employed. First, break down large areas into smaller, more manageable sections. This divide-and-conquer approach often leads to more accurate overall estimates. Second, use reference points or known measurements as benchmarks. For example, knowing the size of a standard object can help in estimating larger areas.
Practicing with various shapes and sizes can also enhance estimation skills. Regular exposure to different scenarios builds intuition and improves the ability to make quick, accurate assessments. Additionally, understanding basic geometric principles and formulas can provide a solid foundation for more complex estimations.
It's also beneficial to cross-check estimates using different methods. For instance, combining visual estimation with rough calculations can lead to more reliable results. Finally, always consider the margin of error in estimations and communicate this clearly when presenting results.
In conclusion, area estimation is a versatile problem-solving tool with wide-ranging applications in real-life situations. From home improvement to scientific research, this technique offers practical solutions when exact measurements are unnecessary or impractical. By understanding its applications and continually refining estimation skills, individuals can make more informed decisions and improve efficiency in various aspects of life and work.
Common Mistakes and How to Avoid Them
When calculating or estimating area and perimeter, students often encounter several common mistakes. Understanding these errors and learning strategies to avoid them is crucial for developing strong problem-solving skills in mathematics. One frequent mistake is confusing area with perimeter. Students may add all sides of a shape to find its area or multiply length by width to calculate perimeter. To prevent this, it's essential to reinforce the definitions: area is the space inside a shape, while perimeter is the distance around it.
Another common error is using incorrect units or forgetting to include units in the final answer. For example, a student might correctly calculate the area of a rectangle as 24 but fail to specify "square units." To avoid this, encourage students to always write units in their calculations and final answers. When working with composite shapes, students sometimes overlook certain sections or double-count areas. A helpful strategy is to break down complex shapes into simpler ones and calculate each part separately before combining the results.
Misreading or misinterpreting problem statements can lead to incorrect calculations. Students might use the wrong dimensions or apply the wrong formula. To combat this, teach students to underline key information in the question and draw a quick sketch of the shape with labeled dimensions. This visual representation can help clarify the problem and reduce errors. When estimating, a common mistake is rounding numbers too early in the calculation process, leading to significant inaccuracies. Encourage students to perform all calculations before rounding the final answer.
Let's consider some examples to illustrate correct and incorrect approaches. For a rectangle with length 8 cm and width 5 cm, an incorrect approach for area might be 8 + 5 = 13 cm (confusing with perimeter). The correct calculation is 8 × 5 = 40 cm². For perimeter, an incorrect method might be 8 × 5 = 40 cm (confusing with area), while the correct approach is 2(8 + 5) = 26 cm. In a more complex scenario, consider an L-shaped figure formed by a 4x4 square attached to a 2x6 rectangle. An incorrect area calculation might simply multiply 6 × 6 = 36, overlooking the missing section. The correct approach is to calculate (4 × 4) + (2 × 6) = 16 + 12 = 28 square units.
To reinforce understanding and prevent these common errors, encourage students to check their work, use estimation to verify if their answer is reasonable, and practice explaining their problem-solving process. By developing these habits and being aware of potential pitfalls, students can improve their accuracy and confidence in calculating area and perimeter.
Conclusion
In this lesson, we've explored the essential concepts of area and perimeter estimation. We've learned how to use grid squares to approximate the size of irregular shapes, a skill that's invaluable in real-world applications. Remember, the key to mastering these techniques is practice. Try estimating areas and perimeters of various objects around you, from simple rectangles to complex, curved shapes. Don't forget to revisit the introduction video for a visual refresher on these methods. Understanding estimation is crucial in many fields, from architecture to landscaping. By honing your estimation skills, you're developing a practical mathematical tool that will serve you well in numerous situations. Keep challenging yourself with different shapes and grid sizes to improve your accuracy. With consistent practice, you'll find yourself becoming more confident and precise in your estimations, a skill that will prove useful throughout your academic and professional life.
Introduction to Calculating and Estimating Area and Perimeter: Estimating Area for Triangles (Using Unit Squares)
In this guide, we will walk through the process of estimating the area of triangles using unit squares. This method is particularly useful when dealing with shapes on grid paper. By following these steps, you will be able to estimate the area of triangles accurately.
Step 1: Understanding Unit Squares
Before we dive into estimating the area of triangles, it's essential to understand what unit squares are. Unit squares are perfect squares that measure one centimeter on all edges. These squares are used as a reference to measure the area of various shapes. When we talk about the area, we refer to the space covered by these unit squares.
Step 2: Counting Unit Squares for Simple Shapes
For simple shapes like rectangles or squares, estimating the area is straightforward. You count the number of unit squares that fit within the shape. For example, if a shape covers four unit squares, its area is four square centimeters. This method works well for shapes that align perfectly with the grid.
Step 3: Introducing Triangles
Now, let's move on to triangles. Triangles can be a bit more challenging because they don't always align perfectly with the grid. To estimate the area of a triangle, we need to use a different strategy. We'll start by looking at right-angle triangles, which are easier to work with.
Step 4: Estimating the Area of Right-Angle Triangles
To estimate the area of a right-angle triangle, we can use the fact that it is half of a rectangle. If you have a unit square and you draw a diagonal line from one corner to the opposite corner, you divide the square into two right-angle triangles. Each of these triangles is half of the unit square. Therefore, the area of a right-angle triangle is half a unit square or 0.5 square centimeters.
Step 5: Applying the Concept to Complex Shapes
When dealing with more complex shapes that include triangles, we can break them down into smaller, more manageable parts. For example, if a shape consists of multiple right-angle triangles, we can estimate the area of each triangle separately and then sum them up. If a shape has two right-angle triangles, each with an area of 0.5 square centimeters, the total area is 1 square centimeter.
Step 6: Estimating the Area of Non-Right-Angle Triangles
For non-right-angle triangles, the process is similar but requires a bit more estimation. You can still use the unit squares as a reference. Try to visualize how many unit squares the triangle would cover if it were a right-angle triangle. Then, adjust your estimate based on the actual shape of the triangle. This method may not be as precise, but it provides a reasonable approximation.
Step 7: Practice with Examples
To solidify your understanding, practice estimating the area of various triangles using unit squares. Start with simple right-angle triangles and gradually move on to more complex shapes. With practice, you'll become more comfortable with the process and improve your accuracy.
Step 8: Verifying Your Estimates
Whenever possible, verify your estimates by comparing them to the actual area calculated using mathematical formulas. For example, the area of a triangle can be calculated using the formula: Area = 0.5 * base * height. Compare your estimate with the calculated area to see how close you are. This step will help you refine your estimation skills.
Step 9: Using Grid Paper for Accuracy
Using grid paper can significantly improve the accuracy of your estimates. The grid lines provide a visual reference that makes it easier to count unit squares and estimate areas. When working with grid paper, take your time to ensure that your estimates are as accurate as possible.
Step 10: Summary and Key Takeaways
Estimating the area of triangles using unit squares is a valuable skill, especially when working with grid paper. By understanding unit squares, counting them for simple shapes, and applying the concept to triangles, you can estimate areas accurately. Practice regularly, verify your estimates, and use grid paper for better accuracy. With these steps, you'll become proficient in estimating the area of triangles.
FAQs
Here are some frequently asked questions about calculating and estimating area and perimeter:
-
What's the difference between area and perimeter?
Area is the space inside a shape, measured in square units (e.g., square meters). Perimeter is the distance around the outside of a shape, measured in linear units (e.g., meters). For example, a rectangle with length 4m and width 3m has an area of 12 square meters and a perimeter of 14 meters.
-
How do I estimate the area of an irregular shape?
To estimate the area of an irregular shape, overlay it on a grid where each square represents a known unit area. Count the full squares within the shape, then estimate partial squares. Count squares more than half-filled as whole, ignore less than half-filled, and use judgment for about half-filled squares. Sum these up and round to the nearest whole number for your estimate.
-
Why is it important to include units in area and perimeter calculations?
Including units is crucial because they provide context and meaning to the numbers. Without units, it's unclear whether the result is in meters, feet, or any other measure. Always specify square units (e.g., cm²) for area and linear units (e.g., cm) for perimeter to avoid confusion and ensure accurate interpretation of results.
-
How can I improve my accuracy when estimating areas?
To improve accuracy in area estimation: 1) Practice regularly with various shapes and sizes. 2) Use finer grids for more precise estimates. 3) Break complex shapes into simpler geometric forms. 4) Cross-check your estimate using different methods. 5) Always consider the margin of error in your estimations.
-
What are some real-world applications of area and perimeter estimation?
Area and perimeter estimation is used in many fields: 1) Home improvement (estimating paint needed for walls). 2) Landscaping (calculating mulch or grass seed required). 3) Agriculture (assessing crop yields). 4) Real estate (approximating property sizes). 5) Urban planning (estimating space for parks or buildings). These estimations help in quick decision-making and resource planning.
Prerequisite Topics
Understanding the foundation of mathematical concepts is crucial for mastering more advanced topics. When it comes to "Calculating and Estimating Area and Perimeter," one essential prerequisite topic stands out: Conversions involving squares and cubic measurements. This fundamental skill is vital for students to grasp before delving into the intricacies of area and perimeter calculations.
The ability to work with square units is particularly relevant when dealing with area calculations. Area, being a two-dimensional measurement, is expressed in square units such as square meters, square feet, or square centimeters. Students who are proficient in converting between these units will find it much easier to solve problems involving areas of different shapes and sizes.
Moreover, understanding conversions involving squares is essential for comparing areas in different units of measurement. For instance, when faced with a problem that requires converting square meters to square feet or vice versa, students who have mastered this prerequisite topic will be able to tackle such challenges with confidence and accuracy.
In the context of perimeter calculations, while linear measurements are primarily used, the ability to work with conversions involving squares and cubic measurements can still be beneficial. It helps students develop a more comprehensive understanding of spatial relationships and unit conversions, which can be applied to various geometric problems.
Furthermore, as students progress to more complex shapes and three-dimensional objects, the knowledge of cubic conversions becomes increasingly important. This prerequisite topic lays the groundwork for understanding volume calculations, which often go hand-in-hand with area and perimeter in more advanced mathematical concepts.
By mastering conversions involving squares and cubic measurements, students develop critical thinking skills and mathematical fluency that extend beyond simple calculations. They learn to visualize and manipulate spatial relationships, which is crucial for estimating areas and perimeters in real-world scenarios.
In conclusion, the importance of understanding this prerequisite topic cannot be overstated. It serves as a bridge between basic arithmetic and more advanced geometric concepts. Students who invest time in mastering conversions involving squares and cubic measurements will find themselves well-equipped to tackle the challenges of calculating and estimating area and perimeter with greater ease and accuracy. This foundational knowledge not only aids in academic success but also prepares students for practical applications in fields such as architecture, engineering, and design.

