Drawing 3D shapes
Topic Notes
- How to draw 3D shapes by hand
- That the “net” of a 3D shape is what it looks like when it is unfolded to show all faces flat in 2D
- How to draw a net for prisms, pyramids, and curved surface shapes
- How to draw 2D perspectives of 3D shapes (top view, side view, front view)
- How to find the cross section of a 3D shape
Notes:
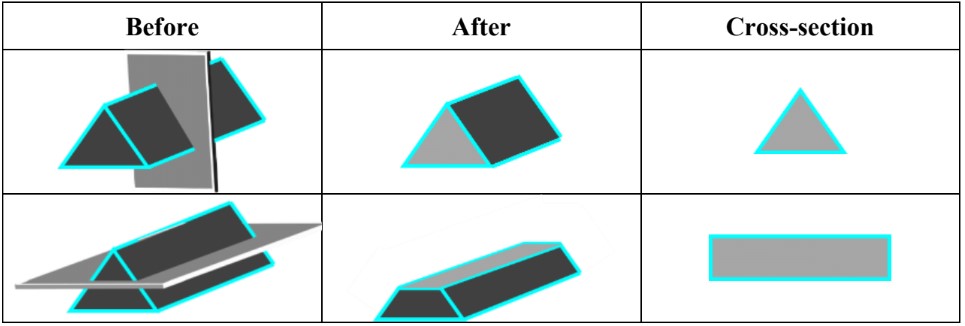
- A net is the 2D pattern that shows all the faces of a 3D shape as if it is unfolded
- Think about what happens when a 3D shape is flattened
- When drawing the net of 3D shapes, start with drawing the base as the 2D shape in your net, then continue adding faces that are connected to each other at different edges as 2D shapes in your net
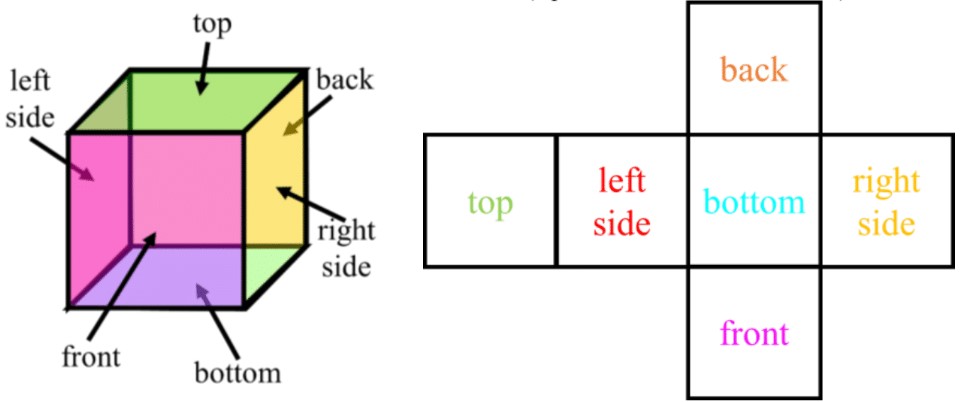
- To draw the net of a prism:
- Recall that for a prism:
- the number of faces (f) is two more than the number of sides in the base (b);
- all the faces (besides the pair of bases) are rectangles
- Ex. the number of faces in a cube is 6 (square base, therefore: )
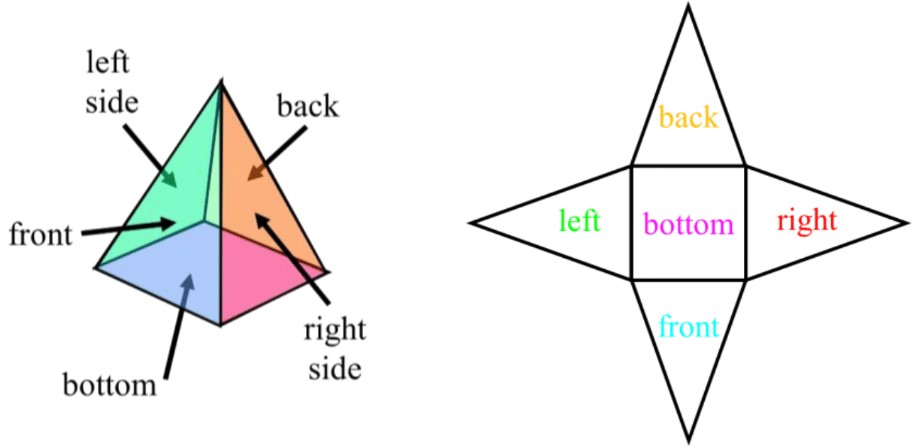
- To draw the net of a pyramid:
- Recall that for a pyramid:
- the number of faces (f) is one more than the number of sides in the base (b);
- all the faces (besides the single base at the bottom) are triangles
- Ex. the number of faces in a rectangular pyramid is 5 (rectangle base: )
- To draw the net of a cylinder :

- To draw the net of a cone:

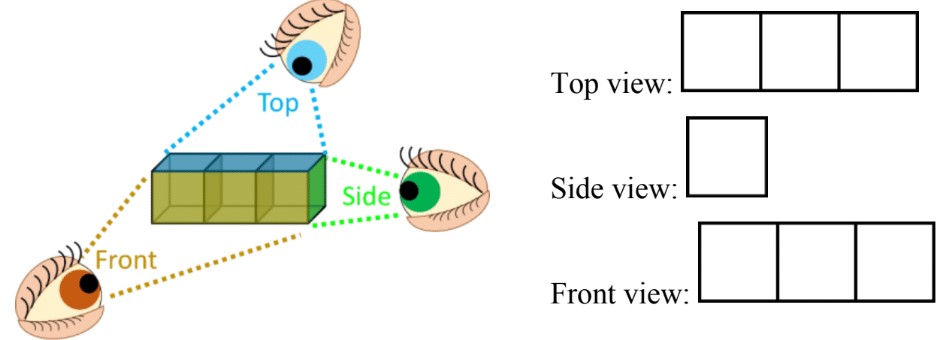
- For 2D perspectives of 3D shapes, draw the 2D faces that only can be seen when viewing the 3D shape from the: top view , side view, or front view.
- The cross section of a 3D shapes is obtained when a flat plane intersects a 3D shape (cuts straight through it).