Sign In
Sign Up
flag-ie

Describing patterns using tables and solving variables

Topic Notes

In this lesson, we will learn:

  • How to describe number patterns using a function table (input output table)
  • How to write formulas with variables for function tables and solve for variables
  • The steps for solving the rule (one-step and two-step) or formula for a function table

Notes:

  • We can think of the relationship between numbers in a pattern as a machine
    • The machine takes the number you give it (the “input”), applies a function (the “rule” or math operations), and gives you a resulting number (the “output”)

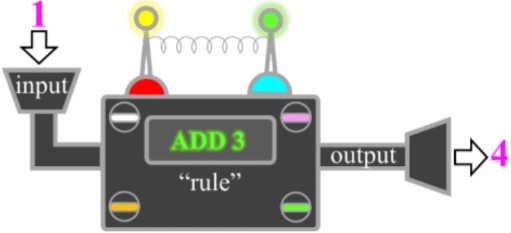
Patterns: Describing Patterns using Tables and Solving Variables

  • The input output table (or function table) keeps track of these inputs and outputs
    • Unlike the number sequence, order is not necessary for a function table
    • Ex. for the number sequence/pattern “start at 1 and add 3 each time” it would be:

Patterns: Describing Patterns using Tables and Solving Variables

    • Ex. but for the function table with a rule of “add 3” it could be:
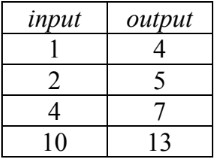
Patterns: Describing Patterns using Tables and Solving Variables

  • It is also possible to have two-step rules for function tables
    • The first step is to either multiply or divide (× or ÷)
    • The second step is to either add or subtract (+ or –)
  • Instead of writing “input” and “output” in the function table, variables can be written instead
    • Variables are symbols (letters) that represent values that can change (“varying”)
    • Variables can be used to write a formula for the function table using the format:
      • (outputvariable)=(multiplier/divisor)x(inputvariable)±(addend/subtrahend) (output variable) = (multiplier/divisor) x (input variable) \pm (addend/subtrahend)
      • Or more commonly written as y=mx+by = m x + b
  • To solve for the variables in function tables:
    • If solving for an output: plug the input value into the formula
    • If solving for an input: plug the output value in and solve backwards (algebra)
  • If you are given a complete function table and asked to solve for the formula:
    • Check horizontally across input/output for one-step rules
    • If it is not a one-step rule:
      • If the inputs are consecutive, the multiplier m (in formula y=mx+by = m x + b) is the difference between outputs
      • If the inputs are random, the formula can be either found by:
        • (#1) trial and error
        • OR (#2) using two pairs of input/output and m is the ratio of ΔyΔx\large\frac{\Delta y}{\Delta x}