Sign In
Sign Up
flag-ie

Coverting between decimals and fractions

0/7
Intros
Start Watching
Lessons
  1. What are the different ways to show decimals?
  2. What are decimal fractions?
  3. How do we convert between decimal fractions and decimals?
  4. What are leading and trailing zeroes?
  5. What are equivalent decimal fractions?
  6. What are non-decimal fractions and how do we convert them into decimals?
  7. How do we show decimal fractions using base ten (block) models?
0/16
Examples
Start Watching
Lessons
  1. Converting between decimals and decimal fractions
    Recall that decimal fractions are fractions with denominators that are powers of 10 (ex. 10, 100, 1000, etc.).
    1. Turn each decimal fraction into a decimal:
      1. 85100\frac{85}{100}
      2. 61000\frac{6}{1000}
      3. 7610\frac{76}{10}
    2. Turn each decimal into a decimal fraction:
      1. .836
      2. 0.4
      3. .75
    3. Use decimal fractions to write this decimal in expanded form: 1.529
  2. Equivalent tenth and hundredth decimal fractions
    Fill in the chart to understand equivalent tenths and hundredths: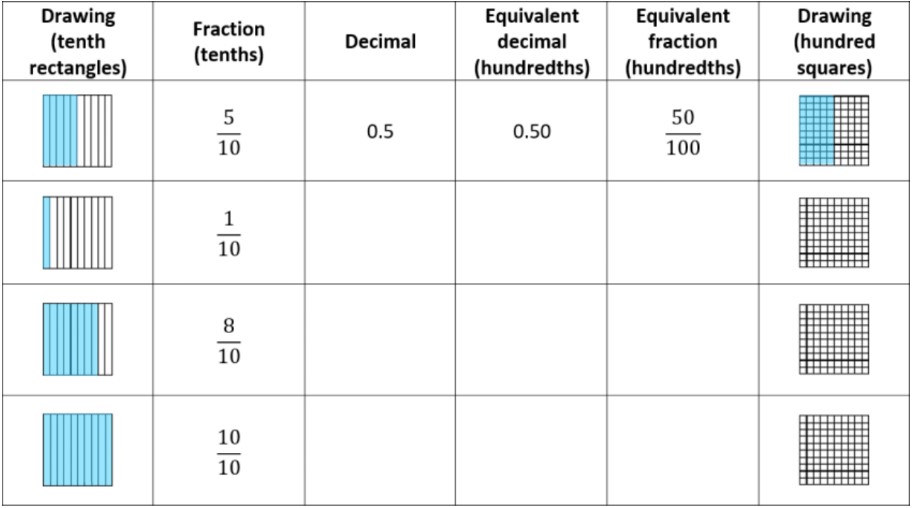

    Decimals: Dividing decimals by power of 10
    1. 110\frac{1}{10}
    2. 810\frac{8}{10}
    3. 1010\frac{10}{10}
  3. Converting between decimals and non-decimal fractions
    Recall that non-decimal fractions are fractions with denominators that are NOT powers of 10 (i.e. any other numbers besides 10, 100, 1000, etc.)
    1. Turn each fraction into a decimal:
      1. 12\frac{1}{2}
      2. 34\frac{3}{4}
      3. 45\frac{4}{5}
      4. 125\frac{1}{25}
    2. Turn each decimal into a fraction in lowest terms:
      1. 0.50
      2. 2.75
      3. 1.08
      4. 3.6
  4. Writing fractions from base ten (block) models
    Write the decimal and fraction represented by the shaded parts of each base ten (block) model:

    1. Decimals: Dividing decimals by power of 10

    2. Decimals: Dividing decimals by power of 10

    3. Decimals: Dividing decimals by power of 10

    4. Decimals: Dividing decimals by power of 10

    5. Decimals: Dividing decimals by power of 10
  5. Decimals and fractions word problem:
    Jimmy and his friends are drinking juice together. After 10 minutes, they measure how much juice they each have left over in their cups and turn those amounts into decimal fractions. Who changed their decimals into fractions correctly?
    1. Jimmy's glass has 0.2 L of orange juice and he says, "that's a fraction of 0.20 L".
    2. Noah has 0.68 L of apple juice in his glass and he says, "that's a fraction of 6810\frac{68}{10}".
    3. Ben has 0.075 L of mango juice and he says, "that's a fraction of 751000\frac{75}{1000}".