Sign In
Sign Up
flag-ie

Distributive property

Topic Notes

Notes:

  • The distributive property is what happens when you multiply a number (called a multiplier or factor) with a sum of two or more numbers (addends inside of brackets).
    • Ex. 2 × (9 + 5) =

  • To distribute means to spread out or to hand around
    • So, the distributive property makes you distribute the multiplier
    • The multiplier/factor is distributed (given to) all the addends in brackets
    • Ex. 2 × (9 + 5) = 2×9 + 2×5
      • = 18 + 10 = 28
      • In other words, multiplying a sum of two numbers is equal to the sum of each addend multiplied by the factor

  • A common mistake that many students make with the distributive property is that they do not FULLY distribute the multiplier/factor:
    • Ex. 2 × (9 + 5) the 2 should be multiplied with both addends = 2 × 9 + 2 × 5
      • The common mistake is to only multiply the with the first addend:
        • 2 × (9 + 5) ? 2 × 9 + 5
          • 2 × 9 + 5 = 18 + 5 = 23
      • The correct answer should have been 28; not distributing will give the incorrect answer of 23

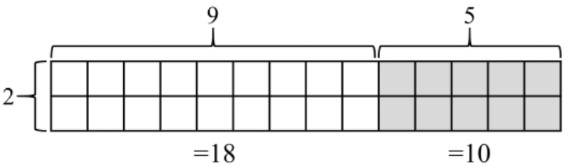
  • The distributive property can be demonstrated using area block models:
    • Area is given by two dimensions (i.e. length × width or height × length)
    • Ex. 2 × (9 + 5) means an area block with a height of 2, and a combined length of 9 and 5. The total number of area blocks is 28.
Representing Numbers: Tally Marks

  • The general formula for the distributive property (where aa, bb and cc are variables that represent real numbers) is:

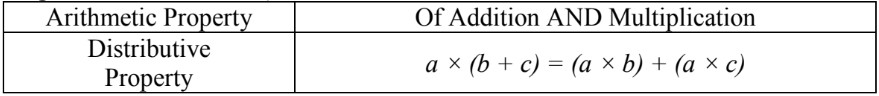
Representing Numbers: Tally Marks

  • The distributive property works for any type of real number as the multiplier and/or addends (such as integers, fractions, and/or decimals):
    • Ex. -3 x (15+35)=(−3 x 15)+(−3 x 35)=−35+−95=−125 (\frac{1}{5} + \frac{3}{5}) = (-3 \,x \, \frac{1}{5}) + (-3 \, x \, \frac{3}{5}) = \frac{-3}{5} + \frac{-9}{5} = \frac{-12}{5}
    • Ex. 5 × (0.2+ 0.05) = (5×0.2) + (5×0.05) = 1.0 + 0.25 = 1.25