Area and perimeter of parallelograms
Topic Notes
In this lesson, we will learn:
- The basic properties of the shape of the parallelogram
- How to understand and calculate the perimeter of a parallelogram
- How to understand and calculate the area of a parallelogram
Notes:
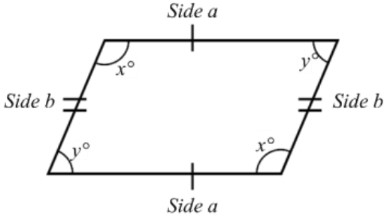
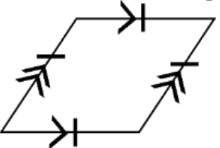
- A parallelogram is a 2D shape with 4 straight sides
- Each pair of sides (across from each other) are parallel and the same length
- The internal angles are not right angles (90°); otherwise it would be a rectangle
- Opposite angles are the same size
- A special parallelogram with all sides of equal length is called a rhombus
- The perimeter is the exact distance around the shape.
- Perimeter is a 1D (one-dimensional) quantity
- It uses units such as meters (m, cm, mm, km), miles (mi), yards (yd), or inches and feet (in and ft)
- For parallelograms, the formula is written as:
- Pparallelogram =
- Where is the length of one of the sides, and is the length of the other side
- The area is the space that is covered by the shape.
- Area is a 2D (two-dimensional) quantity
- It uses squared units such as square meters (m2, cm2, mm2, km2), square miles (mi2), square yards (yd2), or square inches and feet (in2 and ft2)
- For parallelograms, the formula is written as:
- Aparallelogram =
- Where is base, and is height
- A parallelogram’s height is not the same as the slant (side) length.


