Area and perimeter of triangles

In this lesson, we will learn:

• The basic properties of the shape of the triangle
• How to understand and calculate the perimeter of a triangle
• How to understand and calculate the area of a triangle

Notes:

• A triangle is a 2D shape with 3 straight sides and 3 angles that add up to 180°
• There are different types triangles (classified by side lengths or angle size), but it does not change the formulas for area and perimeter.


• The perimeter is the exact distance around the shape.
• Perimeter is a 1D (one-dimensional) quantity
• It uses units such as meters (m, cm, mm, km), miles (mi), yards (yd), or inches and feet (in and ft)


• For triangles, the formula is written as:
• P_triangle = side₁ + side₂ + side₃


• This formula does not change for different types of triangles

• The area is the space that is covered by the shape.
• Area is a 2D (two-dimensional) quantity
• It uses squared units such as square meters (m², cm², mm², km²), square miles (mi²), square yards (yd²), or square inches and feet (in² and ft²)


• For triangles, the formula is written as:
• Area_triangle = $\large \frac{b \, \times \, h} {2}$
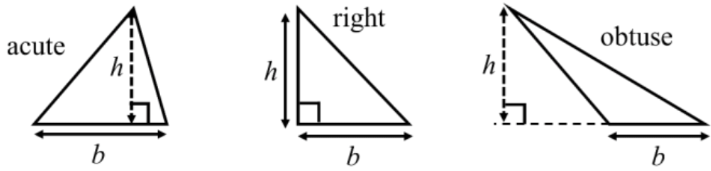
• Where $b$ is base, and $h$ is height


• This formula does not change for different types of triangles, but you do need to keep in mind how to find the triangle’s height
• The triangle’s base is any of the three straight sides
• The triangle’s height is found by placing the chosen base as the flat bottom, and then drawing a perpendicular line from that until the highest point (vertex); it can also be called the triangle’s altitude