It is possible to represent 3-dimensional shapes into 2-dimensional patterns called nets. If you fold the nets back up, they will be reverted to their original 3-dimensional form. It is way easier to find the surface area and perimeter of a 3D object if we know its net!
Master Nets of 3D Shapes: Unfold Geometry's Secrets Dive into the world of 3D shape nets. Learn to visualize, create, and analyze geometric patterns. Enhance your spatial reasoning and problem-solving skills with our comprehensive guide.
Get the most by viewing this topic in your current grade. Pick your course now.
Intros
Examples
Introduction to Nets of 3-Dimensional Shapes
Welcome to our exploration of nets of 3-dimensional shapes! Nets are fascinating 2-dimensional patterns that, when folded, create 3D objects. Imagine unfolding a box and laying it flat - that's a net! These patterns are crucial for understanding the structure and properties of 3D shapes. They help us visualize how surfaces connect and calculate surface area and perimeter. Our introduction video will guide you through this concept, showing how various 3D shapes unfold into their corresponding nets. You'll see cubes, pyramids, and more come to life! This visual approach makes it easier to grasp the relationship between 2D and 3D geometry. As we progress, you'll learn to recognize and draw nets for different shapes, a skill that's invaluable in fields like engineering, architecture, and packaging design. Let's embark on this exciting journey into the world of 3-dimensional shapes and their nets!
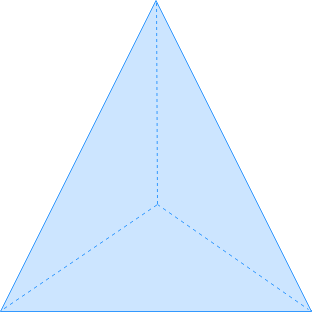
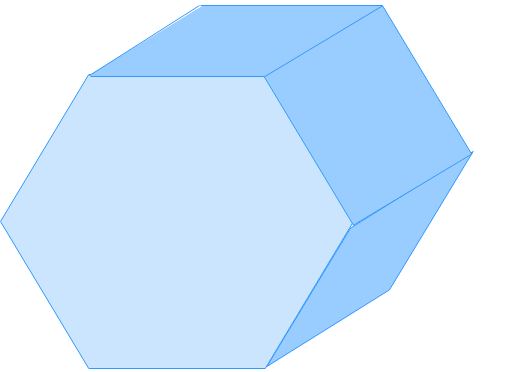
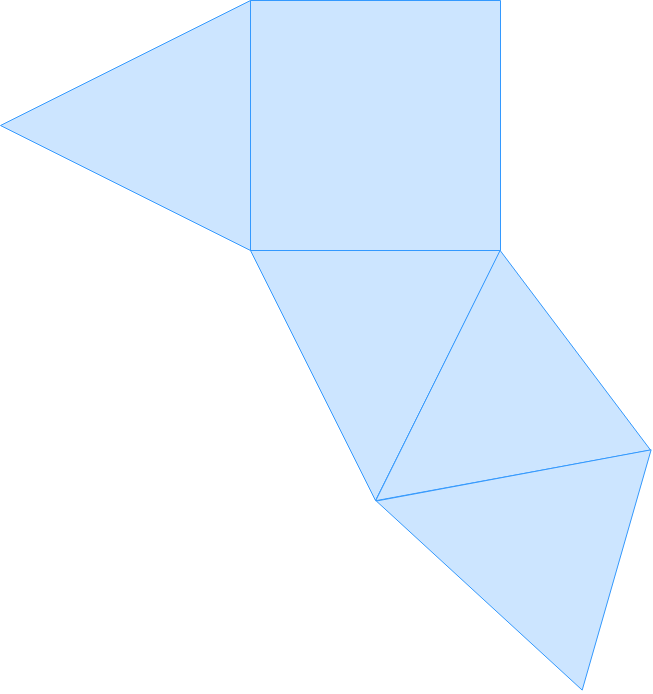
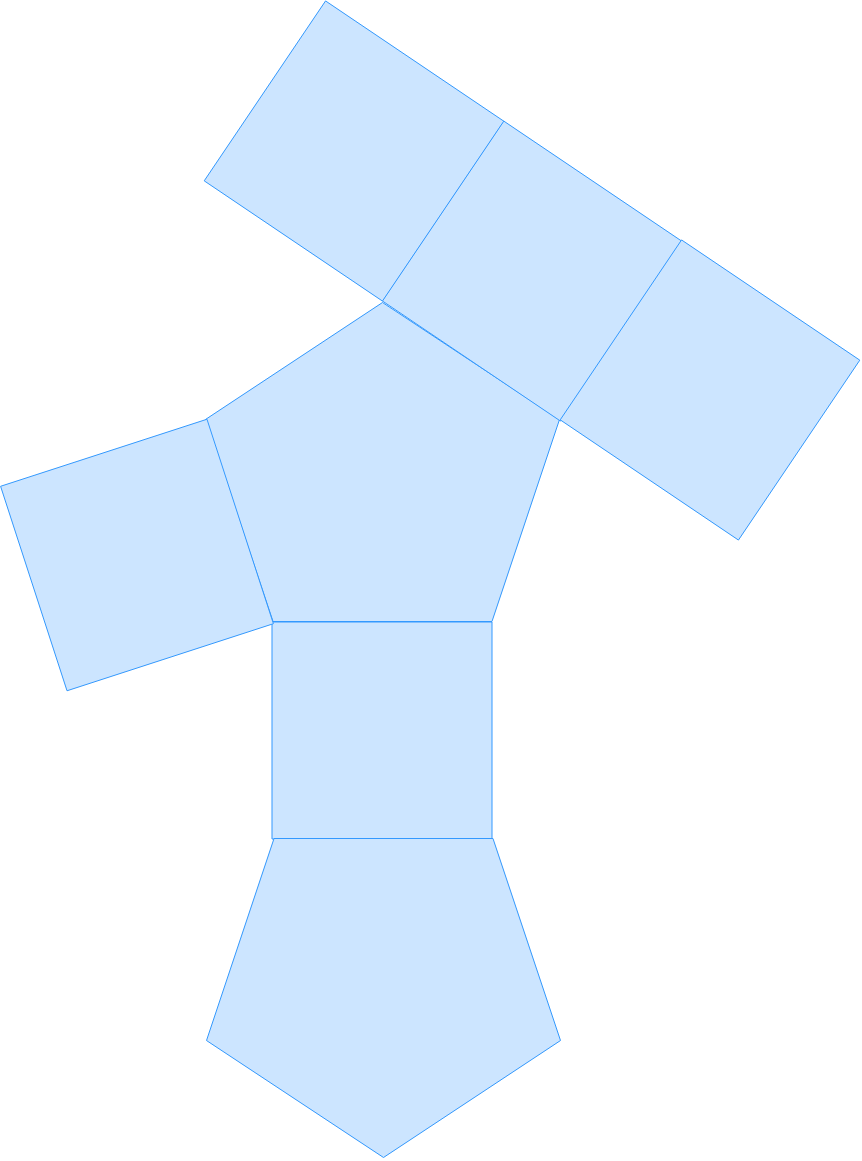
Sketch a net for the objects below.
Step 1: Understand the Shape
First, it's important to understand the shape we are dealing with. In this case, we have a triangular prism. A triangular prism has two triangular bases and three rectangular faces connecting the corresponding sides of the triangles. Imagine you have this 3D shape in front of you and you want to unwrap it to form a 2D net.
Step 2: Identify the Components
Next, identify the components of the triangular prism. There are two triangular faces and three rectangular faces. For simplicity, let's assume the triangular faces are equilateral triangles, meaning all sides are of equal length. This will help in visualizing and drawing the net accurately.
Step 3: Draw the Triangular Faces
Start by drawing one of the triangular faces. Since the prism has two triangular faces, draw another identical triangle. Place one triangle at the top and the other at the bottom of your drawing space. These triangles represent the front and back faces of the prism.
Step 4: Draw the Rectangular Faces
Now, draw the three rectangular faces. These rectangles connect the corresponding sides of the two triangles. Place one rectangle between the two triangles, representing the bottom face of the prism. Then, draw two more rectangles on either side of the bottom rectangle. These represent the side faces of the prism.
Step 5: Connect the Faces
Ensure that all the faces are connected properly. The two triangles should be connected to the three rectangles. The bottom rectangle connects to the base of both triangles, and the side rectangles connect to the sides of the triangles. This forms a continuous net that can be folded back into the original 3D shape.
Step 6: Verify the Net
Finally, verify your net by mentally folding it back into the triangular prism. Ensure that all faces align correctly and that the net forms the original 3D shape without any gaps or overlaps. If everything aligns correctly, you have successfully sketched the net of the triangular prism.
What is a 3 dimensional shape?
A 3 dimensional shape, or 3D shape, is an object that has length, width, and height. Unlike 2D shapes which are flat, 3D shapes occupy space and have volume. Examples include cubes, spheres, cylinders, and pyramids.
How to explain 3D shapes for kids?
To explain 3D shapes to kids, use everyday objects as examples. A ball is a sphere, a box is a cuboid, and an ice cream cone is a cone. Encourage them to touch and hold these objects to feel their depth. Use simple terms like "sides" and "corners" to describe features, and compare 3D shapes to 2D shapes they already know.
What are the 2 and 3 dimensional shapes?
2D shapes are flat and have only length and width, such as circles, squares, triangles, and rectangles. 3D shapes have length, width, and height, giving them volume. Examples of 3D shapes include cubes, spheres, cylinders, cones, and pyramids. The key difference is that 3D shapes occupy space, while 2D shapes do not.
What are the names of 3 dimensional shapes?
Common 3D shapes include: cube, cuboid (rectangular prism), sphere, cylinder, cone, pyramid, prism, tetrahedron, octahedron, and dodecahedron. More complex shapes include torus, ellipsoid, and various polyhedra. Each shape has unique properties in terms of faces, edges, and vertices.
How To Describe 3D Shapes?
To describe 3D shapes, focus on their key features: faces (flat surfaces), edges (where faces meet), vertices (corners), and overall form. Mention the shape of the faces (e.g., square faces on a cube), the number of faces, edges, and vertices. For curved shapes like spheres or cylinders, describe their circular or curved surfaces. Also, note any symmetry or unique characteristics of the shape.
Understanding the foundation of any mathematical concept is crucial for mastering more advanced topics. When it comes to studying nets of 3-dimensional shapes, having a solid grasp of prerequisite topics is essential. One of the most important prerequisites for this subject is the surface area of prisms. This fundamental concept plays a pivotal role in comprehending how 2D representations of 3D shapes work and why they are so important in geometry.
The study of nets of 3-dimensional shapes is an exciting and practical area of geometry that bridges the gap between two-dimensional and three-dimensional thinking. To fully appreciate and understand this topic, students must first become proficient in calculating and conceptualizing the surface area of prisms. This prerequisite knowledge forms the backbone of working with nets, as it provides the necessary skills to visualize how flat surfaces come together to create three-dimensional objects.
When we talk about the surface area calculation of prisms, we're essentially discussing the total area of all the faces of a 3D shape. This concept is directly related to nets because a net is nothing more than the unfolded version of these faces laid out flat. By understanding how to calculate surface area, students gain insight into the relationship between the 2D representation (the net) and the 3D object it forms.
For instance, when working with the net of a cube, students who are well-versed in surface area calculations can quickly recognize that the six equal squares in the net correspond to the six faces of the cube. They can apply their knowledge of surface area to verify that the total area of the net matches the surface area of the resulting 3D shape. This connection between surface area and nets is crucial for developing spatial reasoning skills and geometric intuition.
Moreover, the study of surface area of prisms introduces students to the concept of lateral and total surface area. This distinction becomes particularly relevant when working with nets, as it helps in understanding which parts of the net represent the lateral faces and which represent the bases of the 3D shape. Such knowledge is invaluable when constructing or analyzing nets of more complex prisms and other polyhedra.
Another important aspect of studying surface area as a prerequisite is that it familiarizes students with the properties of different 2D shapes that make up the faces of 3D objects. This knowledge is directly applicable when working with nets, as students need to recognize and manipulate these 2D shapes to form accurate representations of 3D objects. For example, understanding how to calculate the area of rectangles, triangles, and other polygons is essential when dealing with nets of various prisms and pyramids.
The skills developed while learning about surface area calculations also enhance problem-solving abilities that are crucial for working with nets. Students learn to break down complex shapes into simpler components, a strategy that is directly applicable when analyzing or constructing nets of 3D shapes. This analytical approach is invaluable when students encounter more challenging problems involving nets, such as determining whether a given net can fold into a specific 3D shape or creating nets for irregular polyhedra.
Furthermore, the study of surface area of prisms often involves working with formulas and algebraic expressions. This mathematical foundation is extremely beneficial when students progress to more advanced topics in nets of 3-dimensional shapes. They may need to calculate dimensions of nets based on given surface areas or vice versa, requiring a solid understanding of the relationships between linear measurements and area.
It's also worth noting that the concepts learned in surface area calculations provide a springboard for understanding more advanced topics related to nets, such as volume calculations and cross-sections of 3D objects. As students progress in their geometric studies, they'll find that their foundation in surface area continually supports their learning of new and more complex concepts.
In conclusion, the importance of mastering the surface area of prisms</