Mean Value Theorem
In order to prove the Mean Value theorem, we must first be able to prove Rolle's theorem. This is because the Mean Value theorem is the extension of Rolle's theorem.
Rolle's Theorem
In order to prove Rolle's theorem, we must make the following assumptions:
Let f(x) satisfy the following conditions:
1) f(x) is continuous on the interval [a,b]
2) f(x) is differentiable on the interval (a,b)
3) f(a) = f(b)
Now Rolle's Theorem says that there must be a number c such that a < c < b and f'(c) = 0. In order for this to be true, we must cover all the cases in which this is true. There are three cases in total.
- Case 1: Consider the function f(x) = k on the interval [a,b], where k is a constant. See that differentiating the function will give us:
Since f'(x) = 0 for all values of x, then we can choose any number within the interval [a,b] as c. Hence we found a number c such that a < c < b and f'(c) = 0.
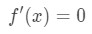
Equation 1: Rolle's Theorem Proof pt.1 - Case 2: Consider some number k in the interval [a,b] such that f(k) > f(a) = f(b). If f(x) is continuous, then that means there exists a maximum at point c. Since we know f(x) is differentiable, then we know that f'(x) exists. Since f'(x) exists and there is a maximum within the interval [a,b], then we know that f'(c) = 0 within [a,b]. In other words, there exists a number c such that a < c < b and f'(c) = 0.
- Case 3: Consider some number k in the interval [a,b] such that f(k) < f(a) = f(b). If f(x) is continuous, then that means there exists a minimum at point c. Since we know f(x) is differentiable, then we know that f'(x) exists. Since f'(x) exists and there is a minimum within the interval [a,b], then we know that f'(c) = 0 within [a,b]. In other words, there exists a number c such that a < c < b and f'(c) = 0.
Since we have proved all three cases, then we have just proved Rolle's theorem.
Now that we have proved Rolle's theorem, then we can continue to prove the Mean Value theorem.
If you are still having trouble understanding the Mean Value theorem, then click on this link for a more detail explanation.
http://tutorial.math.lamar.edu/Classes/CalcI/MeanValueTheorem.aspx
State and Prove the Mean Value theorem
The Mean Value theorem states the following: there exists a number c such that a < c < b and
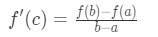
- In order to prove the Mean Value theorem (MVT), we need to again make the following assumptions:
- Let f(x) satisfy the following conditions:
1) f(x) is continuous on the interval [a,b]
2) f(x) is differentiable on the interval (a,b)
Keep in mind Mean Value theorem only holds with those two conditions, and that we do not assume that f(a) = f(b) here.
- Now, consider two points (a, f(a)) and (b, f(b)) in the function. We are going to draw a line between those points and call that the secant line.
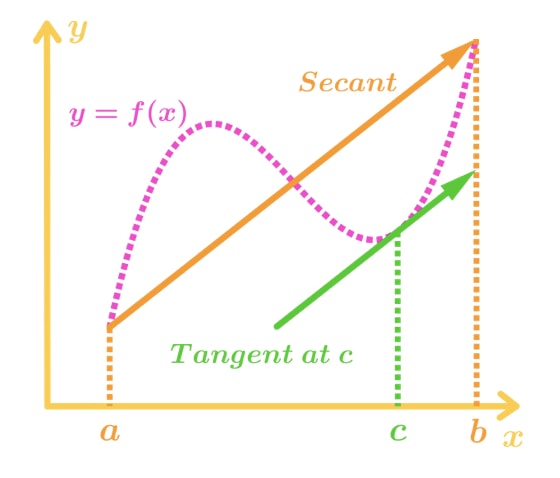
Figure 1: Mean Value Theorem Graph - Now we can create an equation for this secant line. Note that the equation of a line given two points is:
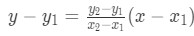
Equation 2: Mean Value Theorem proof pt.1 - So our equation of the secant line is:
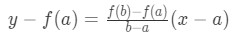
Equation 2: Mean Value Theorem proof pt.2 - And moving f(a) to the other side of the equation will give us:
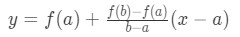
Equation 2: Mean Value Theorem proof pt.3 - Now we are going to create another function called g(x). This function is the subtraction between the function f(x) and the secant line y. In other words,
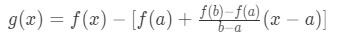
Equation 2: Mean Value Theorem proof pt.4 - Notice that g(x) is also continuous and differentiable because a subtraction of two continuous and differentiable function is still continuous and differentiable. Hence, we can take the derivative. Taking the derivative will give us:
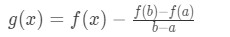
Equation 2: Mean Value Theorem proof pt.5 - Now we have to somehow relate this to Rolle's Theorem. How? Well, Rolle's Theorem holds for three conditions, but we only have two. In other words, we know that g(x) is continuous and differentiable, but we are missing the condition where g(a) = g(b). Let's see if this is true.
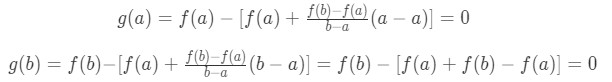
Equation 2: Mean Value Theorem proof pt.6 - Notice that g(b) = g(a), and so g(x) satisfies the three conditions of Rolle's Theorem. Hence, we know that there exists a number c such that g'(c) = 0 within the interval [a,b]. We can use this fact for g'(x). Recall that g'(x) was
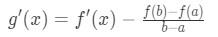
Equation 2: Mean Value Theorem proof pt.7 - So if g'(c) = 0, then
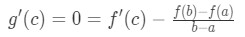
Equation 2: Mean Value Theorem proof pt.8 - This would imply that
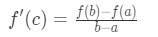
Equation 2: Mean Value Theorem proof pt.9 - Some people actually relate the right side of the equation as the difference quotient. This is because
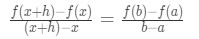
Equation 2: Mean Value Theorem proof pt.10 If b = x + h and a = x.
Mean Value Theorem for Derivatives Examples
Since we have proved the mean value theorem, why don't we do a question which uses this theorem? For example, let
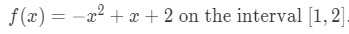
- Using the Mean Value Theorem will give us:
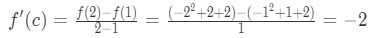
Question 1: Mean Value Theorem Derivative pt.2 - Note that:
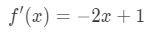
Question 1: Mean Value Theorem Derivative pt.3 - So that means
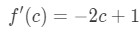
Question 1: Mean Value Theorem Derivative pt.4 - Hence we know that:
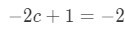
Question 1: Mean Value Theorem Derivative pt.5 - Solving for the number c will give us:
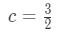
Question 1: Mean Value Theorem Derivative pt.6
Mean Value Theorem for Integrals Example
- The Mean Value theorem can also be used for integrals. We change the formula so that it becomes the following:
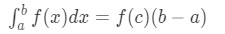
Question 2: Mean Value Theorem Integral pt.1 - However, we interpret this a little differently. For integrals, this theorem tells us that there is a number c within the interval [a,b] such that
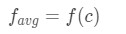
Question 2: Mean Value Theorem Integral pt.2 where f_avg is the average value of the function.
- For example, let us reuse our example again,
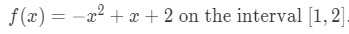
Question 2: Mean Value Theorem Integral pt.3 - And find the mean value of this function. Using the formula will give us:
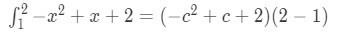
Question 2: Mean Value Theorem Integral pt.4 - Taking the integral on the left side will give us:
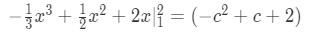
Question 2: Mean Value Theorem Integral pt.5 - Simplifying the left side will give:
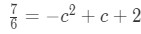
Question 2: Mean Value Theorem Integral pt.6 - Changing the equation a little bit leads us to have
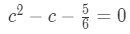
Question 2: Mean Value Theorem Integral pt.7 - Using the quadratic equation to solve for c:
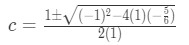
Question 2: Mean Value Theorem Integral pt.8 - This will give us two c values, which are

Question 2: Mean Value Theorem Integral pt.9 - Notice that the first one isn't within the interval [1,2], so we only take the second one. Hence we can conclude that the number c is
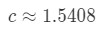
Question 2: Mean Value Theorem Integral pt.10
Intermediate Value theorem
This theorem may not seem very useful, and it isn't even required to prove Rolle's Theorem and the Mean Value theorem. However, this theorem is useful in a sense because we needed the idea of closed intervals and continuity in order to prove the other two theorems. This is why it is relatable.
The intermediate value theorem says the following:
Suppose f(x) is continuous in the closed interval [a,b] and N is a number between f(a) and f(b) . Then there exists a number c where a < c < b, such that f(c) = N. To visualize this, look at this graph.
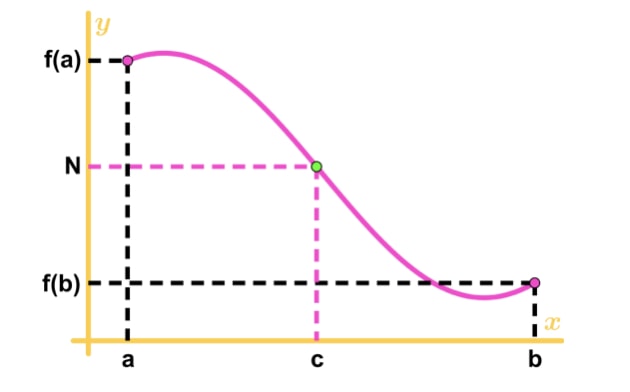
See that N is between f(a) and f(b), and also a < c < b. Hence we know it is possible that f(c) = N.
Let's use this theorem for the following example:
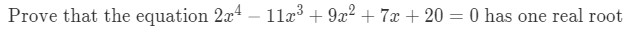
Click on this link to get a full step by step solution of this question.
Mean Value theorem vs Intermediate Value theorem vs Rolle's theorem
Since we know all the theorems, what is the difference between them?
The intermediate value theorem tells us that there is a number c within [a,b] such that f(c) = N is between f(a) and f(b).
The Rolle's theorem tells us that there is a number c within [a,b] where the tangent slope at point c is 0
(f'(c) = 0).
The Mean Value theorem tell us that there is a number c such that the tangent slope of point c is equal to the secant line slope.






