Angle bisectors

What is a bisector

The definition of a bisector is something that cuts an object into two equal parts. This "something" is usually a line or a segment.

What is an angle bisector

What is an angle bisector? The angle bisector definition tell us that this is when a line divides an angle into two congruent angles. These congruent angles can help us determine useful information from different figures. The figure may be a telling us to find the angle bisector of a triangle, but it could just be an angle itself that's not enclosed by a triangle.

The angle bisector theorem tells us that if a point is on an angle bisector, it is then equidistant from the sides of the angle. The reverse is also true in that if a point is equidistant from the sides of the triangle, then it is on the bisector of the angle.

How to bisect an angle

There are certain steps to follow to help you properly draw an angle bisector. We'll run through them with you here.

Firstly, draw an arc centered at the vertex of the angle you're trying to bisect. It must intersect (that is, cross) both sides of the angle, but can be any length. Let's call these two sides where the arc intersects the figure $A$ and $B$.

Then, draw two more arcs. Each of these arcs will respectively be centered with points $A$ and $B$. These two arcs must have the same radius and must intersect one another at point $C$.

For the third and last step, draw a line that crossed through the vertex and point $C$. When you're done this, you'll find the angle bisector for your angle, which is the line that runs through the vertex and point $C$. You've bisected an angle!

Example problems

Let's try what we just learned on some example problems.

Question 1:

Draw the angle bisector of angle $HIJ$. Then, measure and record the two angles made by the angle bisector.

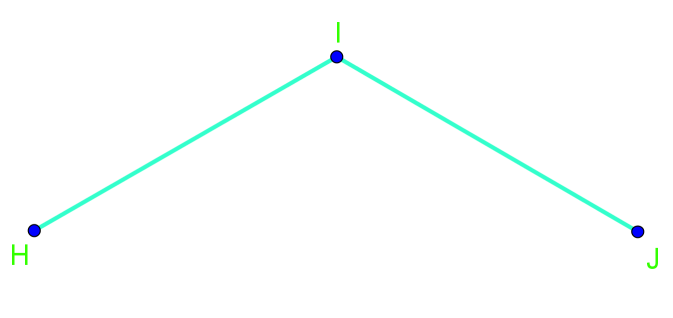
Solution:

First, measure angle $HIJ$. In the video, we get $110$ degree.

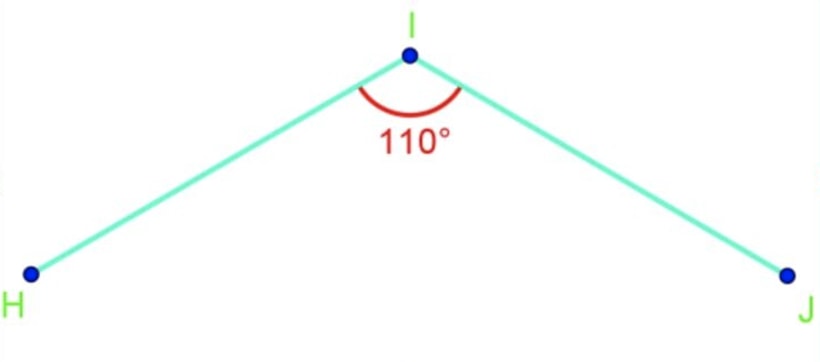
Then divide $110$ degree by $2$, giving us $55$ degree.

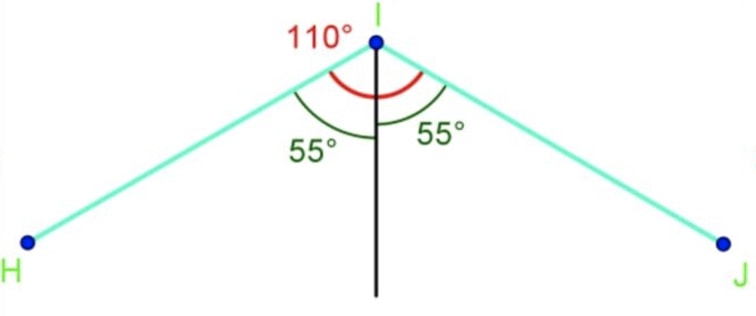
(Here is one way of getting the $55$ degree:)

We measure angle $HIJ$ again, but this time stop at $55$ degree and draw a line at $55$ degree. And then we've got this:

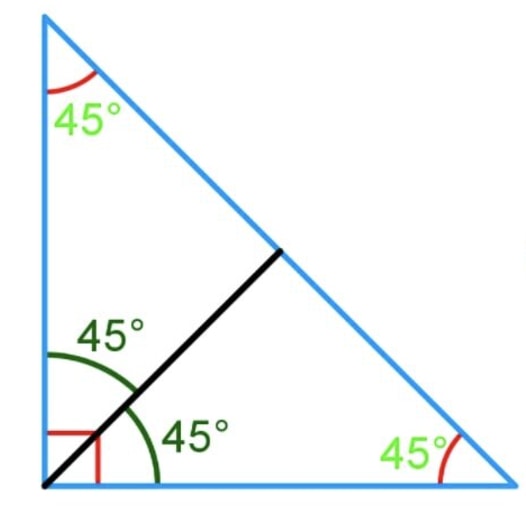
Question 2:

Sarah is getting ready to start quilting a new blanket. She has cut a triangle out of the fabric as shown below. Now, she wants to cut the triangle in half. Show how she can do this using an angle bisector.

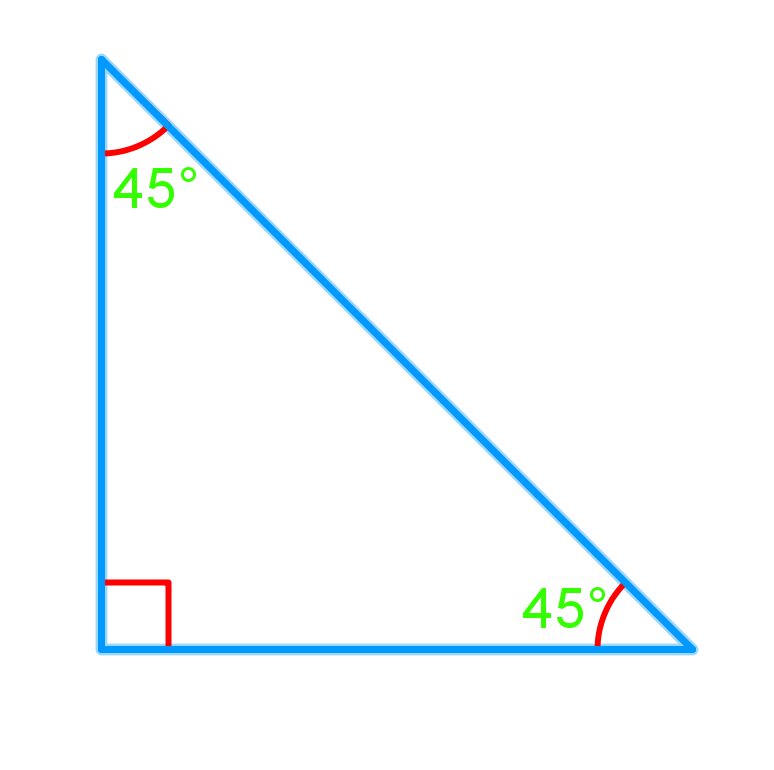
Solution:

We want to cut the triangle in half using an angle bisector. First, we need to determine which angle in the triangle to use the angle bisector. In order to cut the triangle in half, the $90$ degree angle is the one to cut so that it will give us even shapes after we bisect it. So we measure the right angle and cut it right at $45$ degree with the angle bisector. We can cut the triangle exactly in half.

If you wanted a proof of the angle bisector theorem, here's a good interactive demo that allows you to drag points around to change the angle and see what happens to the angle bisector.

Feel free to take a look at perpendicular bisectors and parallel plus perpendicular line segments to further solidify your understanding of this lesson.