Reflections and rotations of shapes
Topic Notes
In this lesson, we will learn:
- How to draw reflections on a grid with vertical, horizontal, or diagonal mirror lines
- How to find order of rotational symmetry for shapes with multiple symmetry lines
- How to rotate shapes around a point 90°, 180°, 270°, and 360° clockwise or counter-clockwise
Notes:
- For line symmetry, a mirror test check if reflected halves match
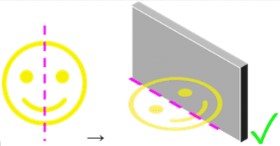
- When drawing reflections of shapes, a grid and a line of symmetry are used
- For reflections, the line of symmetry will be called the “mirror line” instead
- There can be vertical, horizontal, and diagonal mirror lines
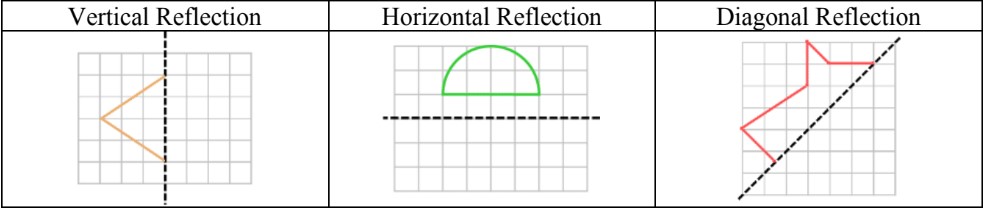
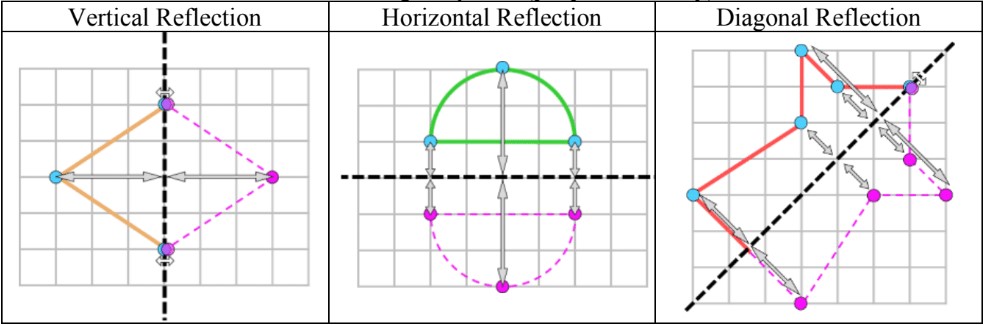
- Choose some exact points of the original shape on the grid
- To draw the reflection of these points, they must be the same distance away from the mirror line as the original points (perpendicularly)
- Another type of symmetry is called rotational symmetry
- If a shape has multiple lines of symmetry: when you spin it around in a full circle (360°), it will look exactly the same more than once
Ex. a triangle has 3 lines of symmetry; rotating a full circle, it matches the original 3 times

- Therefore, the order of rotational symmetry for this regular triangle is = 3
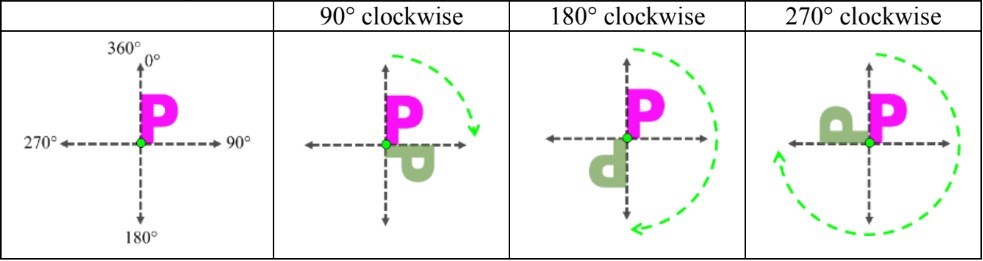
- When rotating shapes, the shape will be spun around a point (usually the middle):
- either clockwise or counter-clockwise
- To one of 4 main rotation angles: 90°, 180°, 270°, and 360°
Ex. Rotate the shape of the letter “P” clockwise 90°, 180°, and 270° around the point
Introduction
Welcome to our lesson on reflections and rotations of shapes! This fascinating topic builds upon our previous discussions of shapes and symmetry, taking our understanding to a new level. We'll begin with an essential introduction video that lays the groundwork for these transformations. Reflections involve flipping a shape over a line, creating a mirror image, while rotations involve turning a shape around a fixed point. These concepts are crucial in geometry and have practical applications in art, design, and architecture. As we explore reflections and rotations, you'll discover how they preserve a shape's size and form while changing its orientation or position. This lesson will help you visualize these transformations and understand their properties. By the end, you'll be able to identify and describe reflections and rotations in various contexts, enhancing your spatial reasoning skills. Let's dive in and uncover the captivating world of geometric transformations!
Understanding Reflections
Reflections are a fundamental concept in geometry that play a crucial role in understanding symmetry and spatial relationships. At its core, a reflection is a transformation that produces a mirror image of an object across a line or plane. This line is known as the line of symmetry or mirror line.
Line symmetry, also called reflection symmetry, is a key aspect of reflections. It occurs when one half of a shape or object is the mirror image of the other half. The line of symmetry divides the shape into two identical parts that are exact mirror images of each other. This concept is not only important in mathematics but also in art, architecture, and nature.
To identify lines of symmetry, two common tests are used: the folding test and the mirror test. The folding test involves imagining or physically folding a shape along a line. If the two halves match perfectly when folded, that line is a line of symmetry. The mirror test, on the other hand, involves placing a mirror along a potential line of symmetry. If the reflection in the mirror completes the original shape, then that line is indeed a line of symmetry.
When working with reflections on a grid, the mirror line serves as the axis of reflection. For example, if we have a triangle on one side of the mirror line, its reflection will appear on the opposite side, with each point of the triangle the same distance from the mirror line as its corresponding point on the original shape. This creates a perfect mirror image.
To draw reflections of shapes, follow these step-by-step instructions:
- Draw the original shape on one side of the mirror line.
- For each vertex of the shape, measure its perpendicular distance from the mirror line.
- Draw a corresponding point on the opposite side of the mirror line, maintaining the same perpendicular distance.
- Connect these new points to form the reflected shape.
- Verify that each point of the reflected shape is the same distance from the mirror line as its corresponding point on the original shape.
Understanding reflections and line symmetry is essential in various fields. In mathematics, it helps in solving complex geometric problems and understanding transformations. In art and design, symmetry is often used to create balanced and aesthetically pleasing compositions. In nature, many organisms and structures exhibit symmetry, from the wings of a butterfly to the petals of a flower.
Practicing with different shapes and mirror lines on a grid can greatly improve one's ability to visualize and create reflections. Start with simple shapes like triangles or rectangles, and gradually move on to more complex figures. Remember that the distance of each point from the mirror line is key to creating accurate reflections.
In conclusion, reflections and line symmetry are fundamental concepts that help us understand and appreciate the world around us. By mastering the folding test, mirror test, and the process of drawing reflections on a grid, we can develop a deeper understanding of spatial relationships and geometric transformations. Whether you're a student studying geometry, an artist exploring symmetry in design, or simply curious about the mathematical principles that shape our world, understanding reflections is a valuable skill that opens up new perspectives on shape, space, and symmetry.
Exploring Rotations
Rotations are fundamental geometric transformations that involve turning an object around a fixed point or axis. In mathematics, rotations play a crucial role in various fields, including geometry, trigonometry, and physics. Understanding rotations is essential for solving complex problems and visualizing spatial relationships.
There are two primary directions of rotation: clockwise and counterclockwise. Clockwise rotation moves in the same direction as the hands of a clock, while counterclockwise rotation moves in the opposite direction. These terms are essential when describing the orientation and movement of objects in space.
When discussing rotations, we often refer to specific rotation angles. The four main rotation angles are 0°, 90°, 180°, and 270°. A 0° rotation leaves the object in its original position, while a 90° rotation turns the object a quarter of the way around. A 180° rotation flips the object upside down, and a 270° rotation is equivalent to a three-quarter turn.
Let's explore some examples of rotating shapes around a point. Imagine a square centered at the origin of a coordinate plane. If we rotate it 90° clockwise, each vertex will move to a new position. The top-right corner will become the bottom-right, the top-left will become the top-right, and so on. Similarly, rotating a triangle 180° will result in its vertices swapping positions across the center point.
Performing rotations on a coordinate plane involves following specific steps. Here's a step-by-step guide to rotate a point (x, y) around the origin:
- Determine the angle of rotation (θ) and whether it's clockwise or counterclockwise.
- For a clockwise rotation, use the formulas: x' = x cos(θ) + y sin(θ) and y' = -x sin(θ) + y cos(θ).
- For a counterclockwise rotation, use: x' = x cos(θ) - y sin(θ) and y' = x sin(θ) + y cos(θ).
- Calculate the new coordinates (x', y') using the appropriate formulas.
- Plot the new point on the coordinate plane.
To rotate a shape, apply this process to each vertex of the shape. For example, to rotate a triangle 90° counterclockwise around the origin, you would rotate each of its three vertices using the counterclockwise rotation formulas with θ = 90°.
Rotations have numerous practical applications in real-world scenarios. In computer graphics, rotations are used to create animations and 3D models. In engineering, rotations are essential for designing mechanical systems and understanding the movement of objects. Architects use rotations to create symmetrical designs and explore different orientations of structures.
It's important to note that rotations preserve the size and shape of objects. This property makes rotations isometric transformations, meaning they maintain the distance between any two points on the object. This characteristic is particularly useful in geometry proofs and when analyzing the properties of shapes under different orientations.
When working with rotations, it's helpful to use tools like graph paper, protractors, or digital software to visualize the transformations accurately. Practice rotating various shapes and points to develop a strong intuition for how objects behave under different rotation angles.
In more advanced mathematics, rotations can be represented using matrices, which provide a powerful tool for performing multiple transformations efficiently. Understanding the basics of rotations lays the foundation for exploring these more complex concepts in linear algebra and higher-level geometry.
As you continue to study rotations, you'll discover their connections to other mathematical concepts, such as symmetry, periodicity, and trigonometric functions. The ability to visualize and perform rotations is a valuable skill that will enhance your spatial reasoning and problem-solving capabilities across various disciplines.
Rotational Symmetry
Rotational symmetry is a fundamental concept in geometry that describes the property of an object to appear identical after being rotated around a central point or axis. This type of symmetry is distinct from, yet related to, line symmetry (also known as reflection symmetry). While line symmetry involves a shape being identical on both sides of a line, rotational symmetry focuses on how a shape looks the same after being turned.
The relationship between rotational symmetry and line symmetry is interesting. Some shapes possess both types of symmetry, while others may have one but not the other. For instance, a square has both rotational and line symmetry, whereas a figure like the letter "S" has rotational symmetry but no line symmetry.
A key concept in understanding rotational symmetry is the "order of rotational symmetry." This refers to the number of times a shape appears identical during one complete 360-degree rotation. The order is determined by how many distinct positions the shape can be rotated into while maintaining its original appearance.
For example, a square has an order of rotational symmetry of 4. This means that during a full rotation, it appears identical four times (at 0°, 90°, 180°, and 270°). Similarly, an equilateral triangle has an order of 3, as it looks the same three times during a complete turn (at 0°, 120°, and 240°).
Regular polygons are excellent examples to illustrate different orders of rotational symmetry. A regular polygon with n sides will have an order of rotational symmetry of n. Here are some examples:
- An equilateral triangle (3 sides) - Order 3
- A square (4 sides) - Order 4
- A regular pentagon (5 sides) - Order 5
- A regular hexagon (6 sides) - Order 6
As the number of sides in a regular polygon increases, so does its order of rotational symmetry. A circle, which can be thought of as a regular polygon with an infinite number of sides, has an infinite order of rotational symmetry, as it looks the same at any angle of rotation.
It's important to note that not all shapes with rotational symmetry are regular polygons. Many irregular shapes can also exhibit rotational symmetry. For instance, a propeller shape or a swastika has rotational symmetry of order 4, despite not being a regular polygon.
An intriguing aspect of rotational symmetry is that some shapes possess it without having any line symmetry. This special case occurs when an object looks the same after rotation but cannot be divided into two identical halves by any straight line. The letter "S" is a classic example of this phenomenon. It has rotational symmetry of order 2 (it looks the same after a 180-degree rotation) but has no line of symmetry.
Other examples of shapes with rotational symmetry but no line symmetry include:
- The triskelion (a figure with three interlocking spirals)
- Certain spiral patterns
- Some company logos designed to have a sense of motion or rotation
Understanding rotational symmetry is crucial in various fields beyond mathematics. In art and design, it's used to create balanced and aesthetically pleasing compositions. In architecture, rotational symmetry often appears in the design of buildings, particularly in circular or radial structures. In nature, many flowers and organisms exhibit rotational symmetry, which has inspired countless designs in human-made objects.
The concept of rotational symmetry in 3D objects also extends to three-dimensional objects. For instance, a cube has several axes of rotational symmetry, each with different orders. This complexity in 3D rotational symmetry plays a significant role in crystallography and molecular structures.
In conclusion, rotational symmetry is a fascinating geometric property that describes how an object appears unchanged through rotation. Its order indicates the number of identical positions during a full turn. While closely related to line symmetry, rotational symmetry offers unique insights into
Applications and Practice
Reflections and rotations are fundamental geometric transformations with numerous real-world applications. Understanding these concepts is crucial for students as they appear in various fields and everyday situations. Let's explore some practical uses and engage in practice problems to reinforce our understanding.
Real-World Applications
- Architecture: Reflections and rotations are essential in designing symmetrical buildings and structures. Architects use these principles to create aesthetically pleasing and balanced designs.
- Art and Design: Artists and graphic designers utilize reflections and rotations to create patterns, logos, and visually appealing compositions.
- Manufacturing: In industrial settings, understanding rotations is crucial for operating machinery and designing production processes.
- Navigation: GPS systems and mapping applications rely on rotations to provide accurate directions and orientations.
- Computer Graphics: Video game developers and animators use reflections and rotations to create realistic 3D environments and character movements.
Practice Problems
Let's apply our knowledge of reflections and rotations with some practice problems:
Problem 1: Reflection
Reflect the triangle with vertices A(2,3), B(5,1), and C(4,5) over the y-axis.
Solution:
- To reflect over the y-axis, we change the sign of the x-coordinate for each point.
- A(2,3) becomes A'(-2,3)
- B(5,1) becomes B'(-5,1)
- C(4,5) becomes C'(-4,5)
Problem 2: Rotation
Rotate the point P(3,2) 90° counterclockwise around the origin.
Solution:
- For a 90° counterclockwise rotation, use the formula: (x,y) (-y,x)
- P(3,2) becomes P'(-2,3)
Create Your Own Shapes
To further explore symmetry properties, try the following activities:
- Draw a simple shape on graph paper.
- Identify any lines of symmetry in your shape.
- Rotate your shape 90°, 180°, and 270°. Observe how it changes.
- Reflect your shape over the x-axis and y-axis. Compare the results.
Additional Practice
Here are more problems to reinforce your understanding:
Problem 3:
Reflect the quadrilateral with vertices A(1,1), B(3,1), C(4,3), and D(2,4) over the line y=x.
Problem 4:
Rotate the triangle with vertices P(-1,2), Q(3,2), and R(1,5) by 180° around the origin.
Problem 5:
Create a shape with at least one line of symmetry and one rotational symmetry. Describe its symmetry properties.
Remember, practicing these concepts regularly will help you develop a strong intuition for geometric transformations. As you work through these problems, visualize the movements and try to predict the outcomes before calculating. This approach will enhance your spatial reasoning skills, which are valuable in many real-world applications.
For further exploration, consider using online geometry tools or software that allow you to manipulate shapes dynamically. These interactive platforms can provide immediate visual feedback, helping you
Advanced Concepts and Challenges
As we delve deeper into the world of geometric transformations, we encounter more complex concepts that build upon our understanding of basic reflections and rotations. Two particularly intriguing areas are glide reflections and three-dimensional rotations, which offer new perspectives on how shapes can be manipulated in space.
Glide reflections combine two fundamental transformations: a reflection and a translation. In this process, a shape is first reflected over a line, then translated parallel to that line. This creates a unique movement that is neither purely reflective nor purely translational. Glide reflections are often found in nature and art, such as in the patterns of some butterfly wings or in certain types of wallpaper designs.
Moving into three-dimensional space, rotations become even more complex and fascinating. While 2D rotations occur around a point, 3D rotations happen around an axis. This axis can be oriented in any direction within the 3D space, leading to a wide variety of possible transformations. Understanding 3D rotations is crucial in fields like computer graphics, robotics, and aerospace engineering.
When we combine multiple transformations, the complexity and potential for creative problem-solving increase dramatically. For instance, consider a sequence of transformations that includes a reflection, a rotation, and a glide reflection. Determining the final position and orientation of a shape after such a series of transformations requires careful analysis and spatial reasoning skills.
It's important to note the connections between these advanced concepts and other geometric transformations. Translations, for example, can be viewed as a special case of glide reflections where the reflection component is nullified. Dilations, which change the size of a shape, can be combined with rotations to create spiral-like transformations. Understanding these relationships helps in developing a more comprehensive view of geometric transformations as a whole.
Challenging problems in this area often involve determining the sequence of transformations that will map one shape onto another, or predicting the result of a complex series of transformations. These exercises not only test mathematical skills but also enhance spatial reasoning and problem-solving abilities.
For example, consider a problem where you're given a 3D object and asked to determine the sequence of rotations around different axes that will orient it in a specific way. This requires visualizing the object in space and understanding how each rotation will affect its orientation. Another challenging task might involve creating a specific pattern using only glide reflections and rotations, pushing students to think creatively about how these transformations can be combined.
The study of these advanced geometric transformations also opens up connections to other areas of mathematics. Group theory, for instance, provides a framework for understanding the properties of sets of transformations. The concept of symmetry, central to many areas of science and art, is deeply linked to these geometric operations.
As we explore these more complex concepts, it becomes clear that geometric transformations are not just abstract mathematical ideas, but powerful tools for understanding and manipulating the world around us. From the design of mechanical systems to the analysis of crystal structures in chemistry, the principles of reflections, rotations, and their combinations play a crucial role.
By mastering these advanced concepts and tackling challenging problems, students develop not only their mathematical skills but also their ability to visualize and reason about spatial relationships. This knowledge forms a foundation for further study in fields like computer science, physics, and engineering, where understanding complex spatial transformations is often essential.
Conclusion
In this lesson, we explored the fascinating world of reflections and rotations of shapes. The introduction video laid a crucial foundation, helping us grasp these fundamental concepts. We learned how to identify lines of symmetry, perform reflections across various axes, and rotate shapes around specific points. Understanding these transformations is essential for developing spatial reasoning skills and appreciating geometric patterns in our surroundings. As you continue your journey in mathematics, remember to practice these concepts regularly. Look for symmetry in everyday objects, architecture, and nature. Challenge yourself to create your own symmetric designs or predict the outcomes of different transformations. By engaging with these ideas outside the classroom, you'll deepen your understanding and develop a keen eye for geometric relationships. Don't hesitate to explore additional resources or seek help if you encounter difficulties. Your growing knowledge of reflections and rotations will serve as a solid foundation for more advanced geometric concepts in the future.
Introduction to Reflections and Rotations of Shapes: Drawing Reflections (Mirror Images) on a Grid
In this lesson, we will learn how to draw reflections (mirror images) of shapes on a grid. This involves understanding the concepts of symmetry and using a mirror line to create accurate reflections.
Step 1: Understanding Reflections and Symmetry
When reflecting shapes, we use the concept of symmetry. A shape is symmetrical if it can be divided into two congruent parts that are mirror images of each other. The line that divides the shape into these two parts is called the line of symmetry. To test if a line is a line of symmetry, you can use the folding test or the mirror test. In the folding test, you fold the shape along the line and see if both halves match perfectly. In the mirror test, you place a mirror along the line and check if the reflected half matches the original half.
Step 2: Identifying the Mirror Line
In reflections, the line of symmetry is referred to as the mirror line. This line can be vertical, horizontal, or diagonal. The mirror line is crucial as it helps us determine where the reflected image will be placed on the grid. For example, if we have a vertical mirror line, the reflected image will be on the opposite side of the line, maintaining the same distance from the line as the original shape.
Step 3: Drawing Reflections on a Grid
To draw reflections on a grid, follow these steps:
- Identify the mirror line on the grid.
- Mark the key points of the original shape and measure their distances from the mirror line.
- Plot the reflected points on the opposite side of the mirror line, ensuring they are the same distance from the line as the original points.
- Connect the reflected points to form the reflected shape.
For example, if a point on the original shape is three spaces away from the mirror line, its reflected point will also be three spaces away on the opposite side.
Step 4: Example with Vertical Mirror Line
Consider a shape with a vertical mirror line. To reflect this shape:
- Identify the points on the shape that lie on the mirror line. These points will remain unchanged in the reflection.
- For other points, measure their distances from the mirror line and plot their reflections on the opposite side.
- Connect the reflected points to complete the reflected shape.
For instance, if a point is three spaces to the left of the mirror line, its reflection will be three spaces to the right of the mirror line.
Step 5: Example with Horizontal Mirror Line
Now, consider a shape with a horizontal mirror line. To reflect this shape:
- Identify the points on the shape that lie on the mirror line. These points will remain unchanged in the reflection.
- For other points, measure their distances from the mirror line and plot their reflections on the opposite side.
- Connect the reflected points to complete the reflected shape.
For example, if a point is two spaces above the mirror line, its reflection will be two spaces below the mirror line.
Step 6: Example with Diagonal Mirror Line
Finally, consider a shape with a diagonal mirror line. To reflect this shape:
- Identify the points on the shape that lie on the mirror line. These points will remain unchanged in the reflection.
- For other points, measure their distances from the mirror line along the diagonal and plot their reflections on the opposite side.
- Connect the reflected points to complete the reflected shape.
For instance, if a point is one space away from the mirror line along the diagonal, its reflection will be one space away on the opposite side of the diagonal mirror line.
Conclusion
Drawing reflections on a grid involves understanding symmetry and using a mirror line to accurately plot the reflected points. By following the steps outlined above, you can create precise mirror images of shapes on a grid, whether the mirror line is vertical, horizontal, or diagonal.
FAQs
Here are some frequently asked questions about reflections and rotations of shapes:
-
What is the difference between a reflection and a rotation?
A reflection is a transformation that flips a shape over a line (the line of symmetry), creating a mirror image. A rotation, on the other hand, involves turning a shape around a fixed point (the center of rotation) by a specific angle.
-
How do you identify the order of rotational symmetry?
The order of rotational symmetry is the number of times a shape appears identical during one complete 360-degree rotation. To identify it, rotate the shape and count how many times it looks exactly the same as the original position during one full turn.
-
Can a shape have rotational symmetry but no line symmetry?
Yes, it's possible. For example, the letter "S" has rotational symmetry of order 2 (it looks the same after a 180-degree rotation) but has no line of symmetry. Other examples include the triskelion and certain spiral patterns.
-
How do you perform a reflection on a coordinate plane?
To reflect a point over the x-axis, keep the x-coordinate the same and negate the y-coordinate. For reflection over the y-axis, negate the x-coordinate and keep the y-coordinate the same. For reflection over y=x, swap the x and y coordinates.
-
What are some real-world applications of reflections and rotations?
Reflections and rotations are used in various fields such as architecture (designing symmetrical buildings), art and design (creating patterns and logos), manufacturing (operating machinery), navigation (GPS systems), and computer graphics (3D modeling and animation).
Prerequisite Topics
Understanding the foundations of geometry is crucial when delving into the fascinating world of reflections and rotations of shapes. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a solid grasp of basic geometric concepts forms the bedrock for comprehending more advanced transformations.
Before exploring reflections and rotations, students should be comfortable with fundamental geometric principles. A strong understanding of basic shapes and their properties is essential. Familiarity with concepts such as lines, angles, and symmetry provides a sturdy foundation for grasping how shapes can be manipulated in space.
Additionally, knowledge of coordinate geometry is invaluable when working with reflections and rotations. The ability to plot points and visualize shapes on a coordinate plane enhances one's capacity to understand and predict the outcomes of these transformations. This skill set allows students to precisely describe the movement and positioning of shapes during reflections and rotations.
An appreciation for spatial reasoning is another key component in mastering reflections and rotations. This involves the ability to mentally manipulate objects and understand their relationships in space. Developing strong spatial reasoning skills helps students intuitively grasp how shapes change when reflected or rotated.
Furthermore, a basic understanding of algebraic concepts can be beneficial when dealing with more complex reflections and rotations. Simple equations and formulas often come into play when describing these transformations mathematically, making algebraic fluency a valuable asset.
While not always explicitly stated as prerequisites, these foundational topics form the building blocks for a comprehensive understanding of reflections and rotations. By ensuring a solid grasp of these underlying concepts, students can approach the study of shape transformations with confidence and clarity.
As students progress in their exploration of reflections and rotations, they'll find that these transformations are not isolated concepts but are deeply interconnected with other areas of mathematics. For instance, understanding reflections and rotations can enhance one's grasp of symmetry in nature and art, as well as provide insights into more advanced topics like group theory in higher mathematics.
In conclusion, while there may not be a specific list of prerequisite topics for reflections and rotations of shapes, a well-rounded understanding of basic geometric principles, coordinate systems, spatial reasoning, and elementary algebra provides an excellent foundation. By building upon these fundamental concepts, students can more easily navigate the intricacies of shape transformations and appreciate their wide-ranging applications in both mathematics and the world around us.

