Area and perimeter of triangles

Introduction

Welcome to the fascinating world of triangles! In this section, we'll explore the essential concepts of area of triangles and perimeter of triangles, fundamental elements of geometry. Understanding these concepts is crucial for solving various real-world problems with triangles and advancing your mathematical skills. Our introduction video serves as an excellent starting point, providing a clear and engaging overview of the topic. As we delve into the formulas and calculations, you'll discover how these seemingly simple shapes hold a wealth of information. From calculating land areas to designing structures, the principles we'll cover have wide-ranging applications. Whether you're a beginner or looking to refresh your knowledge, this exploration of triangle geometry will equip you with valuable tools for mathematical analysis. So, let's embark on this exciting journey together, unraveling the mysteries of triangular shapes and their measurements!

Understanding the area of triangles is not just about memorizing formulas; it's about seeing the connections between different geometric properties. This knowledge is particularly useful when tackling real-world problems with triangles, such as determining the amount of material needed for construction projects or analyzing the forces acting on a structure. By mastering these concepts, you'll be better prepared to apply mathematical reasoning in practical situations, making you a more effective problem solver in both academic and professional settings.

Understanding Triangles and Dimensions

Triangles are fascinating geometric shapes that play a fundamental role in mathematics and our everyday lives. Let's dive into the world of triangles and explore the concept of dimensions in geometry. By the end of this discussion, you'll have a solid grasp of these essential geometric principles.

First, let's define what a triangle is. A triangle is a two-dimensional (2D) shape with three straight sides and three angles. It's the simplest polygon, meaning it's a closed shape formed by straight lines. The beauty of triangles lies in their simplicity and versatility. You can find triangles in architecture, art, and even in nature.

Now, let's talk about dimensions in geometry. Dimensions refer to the different aspects of measurement we can apply to geometric shapes. In the case of triangles, we primarily deal with one-dimensional (1D) and two-dimensional (2D) measurements, but it's also worth briefly mentioning three-dimensional (3D) concepts.

Let's start with the one-dimensional aspect of triangles: the perimeter. The perimeter is the distance around the outside of a shape. For a triangle, you calculate the perimeter by adding up the lengths of all three sides. It's a linear measurement, which is why we consider it one-dimensional. Imagine walking along the edges of a triangle the total distance you'd travel is the perimeter.

Moving on to two dimensions, we encounter the concept of area. The area of a triangle represents the amount of space it covers on a flat surface. To help visualize this, think about using a highlighter to color in a triangle drawn on paper. The space you fill with the highlighter represents the area. Unlike the perimeter, which is measured in linear units (like inches or centimeters), area is measured in square units (like square inches or square centimeters).

Calculating the area of a triangle is a bit more complex than finding its perimeter. The most common formula is: Area = (base × height) ÷ 2. Here, the base is any side of the triangle, and the height is the perpendicular distance from that base to the opposite vertex (corner point). This formula works for all types of triangles, whether they're right-angled, equilateral, or scalene.

While we're primarily focused on 2D shapes, it's worth briefly mentioning the third dimension: volume. Although triangles themselves don't have volume (they're flat shapes), they play a crucial role in 3D geometry. For instance, a triangular prism or pyramid has volume, and understanding triangles is key to working with these 3D shapes.

Let's look at some real-world examples to illustrate these concepts. Imagine a triangular yield sign on the road. Its perimeter would be the total length of metal used to create its outline. The area would be the amount of paint needed to cover its surface. Now, picture a triangular slice of pizza. The crust represents the perimeter, while the surface of toppings represents the area. If you were to stack multiple slices, you'd start dealing with volume a 3D concept.

Understanding these dimensional concepts is crucial in various fields. Architects use triangles for their structural strength in building designs. Artists employ triangles to create dynamic compositions. In nature, triangles appear in everything from the shape of mountains to the structure of certain molecules.

As you explore the world of geometry further, you'll discover that triangles in trigonometry are the building blocks for many other shapes and concepts. Their properties form the basis of trigonometry, a branch of mathematics with wide-ranging applications in physics, engineering, and computer graphics.

In conclusion, triangles are simple yet powerful 2D shapes that introduce us to fundamental geometric concepts. By understanding the dimensions associated with triangles from the one-dimensional perimeter to the two-dimensional area, and even touching on three-dimensional applications we gain valuable insights into the world of mathematics and its practical applications. Whether you're a student, a professional, or simply curious about the world around you, grasping these concepts will enhance your appreciation for the geometry that shapes our universe.

Calculating the Perimeter of Triangles

Understanding the concept of perimeter is essential when studying triangles in geometry. The perimeter of a triangle is simply the total distance around its outer edge, calculated by adding up the lengths of all three sides. This fundamental principle applies to all types of triangles, whether they're scalene, isosceles, or equilateral.

Let's start with the basic formula for calculating a triangle's perimeter:

Perimeter = Side A + Side B + Side C

This straightforward equation remains consistent regardless of the triangle's shape or size. Now, let's break down how this formula works for different types of triangles:

1. Scalene Triangle: In a scalene triangle, all three sides have different lengths. To calculate its perimeter, you simply add the lengths of all three sides together.

2. Isosceles Triangle: An isosceles triangle has two sides of equal length. The perimeter calculation remains the same add all three sides but you'll notice that two of the values in your equation will be identical.

3. Equilateral Triangle: In an equilateral triangle, all three sides are equal in length. The perimeter formula is still the same, but you'll be adding the same value three times.

Let's walk through an example calculation to illustrate how this works in practice. Imagine we have a scalene triangle with the following side lengths:

Side A = 5 cm
Side B = 7 cm
Side C = 9 cm

To find the perimeter, we simply plug these values into our formula:

Perimeter = 5 cm + 7 cm + 9 cm = 21 cm

So, the perimeter of this scalene triangle is 21 cm. The process would be identical for an isosceles or equilateral triangle; you'd just be working with some repeated values.

It's important to note that while the formula remains constant, the actual calculation of a triangle's perimeter can sometimes be more complex. In some cases, you might not be given the lengths of all sides directly. Instead, you might need to use other geometric principles or trigonometric functions to determine the missing side lengths before you can calculate the perimeter.

For instance, if you're given the length of one side and two angles of a triangle, you'd first need to use the sine law to find the lengths of the other two sides. Only then could you proceed with the perimeter calculation.

Understanding how to calculate a triangle's perimeter is not just an academic exercise. This skill has practical applications in various fields, including construction, landscaping, and design. For example, if you're planning to fence a triangular plot of land, knowing how to calculate its perimeter would be crucial in determining how much fencing material you'd need to purchase.

As you continue your study of geometry, you'll find that this basic principle of perimeter calculation extends to more complex shapes as well. However, the fundamental concept remains the same: the perimeter is always the sum of all sides, regardless of the shape's complexity.

To reinforce your understanding, try practicing with different triangle types and sizes. Start with simple examples where all side lengths are provided, then gradually move on to more challenging problems where you might need to calculate some side lengths first. Remember, the key to mastering this concept is consistent practice and application.

In conclusion, calculating the perimeter of a triangle is a straightforward process once you understand the basic formula. Whether you're dealing with a scalene, isosceles, or equilateral triangle, the approach remains the same: add up the lengths of all three sides. This fundamental geometric principle serves as a building block for more advanced concepts in mathematics and has numerous real-world applications.

Understanding Area of Triangles

When we talk about the area of a shape, we're discussing how much two-dimensional space it occupies. You're probably familiar with calculating the area of a rectangle - it's simply length multiplied by width. But what about triangles? Let's explore how we can understand and calculate the area of these three-sided figures.

Triangles and rectangles are more closely related than you might think. In fact, understanding the area of a triangle starts with understanding the area of a rectangle. Imagine a rectangle, and then draw a diagonal line from one corner to the opposite corner. What do you get? Two equal triangles!

This relationship is key to deriving the formula for a triangle's area. If a triangle is half of a rectangle, then its area must be half of the rectangle's area. This leads us to the formula for calculating the area of a triangle:

Area of a Triangle = (base * height) / 2

Let's break down each component of this formula:

• Base (b): This is the length of one side of the triangle, which we choose as the 'bottom' or base.
• Height (h): Also called altitude, this is the perpendicular distance from the base to the opposite vertex (corner) of the triangle.
• Division by 2: This is because a triangle is half of a rectangle with the same base and height.

To visualize this, imagine a triangle inside a rectangle. The base of the triangle is the same as the width of the rectangle, and the height of the triangle is the same as the height of the rectangle. The triangle takes up exactly half of the rectangle's area.

Here's a simple example: If we have a triangle with a base of 6 units and a height of 4 units, we can calculate its area as follows:

Area = (6 * 4) / 2 = 24 / 2 = 12 square units

It's important to note that any side of a triangle can be considered the base. The height must always be measured perpendicular to the chosen base, from the base to the opposite vertex. This flexibility is useful when working with different triangle orientations.

Understanding the area of triangles is crucial in many real-world applications. Architects use it when designing roofs, engineers when calculating material needs for triangular structures, and even artists when planning compositions. In more advanced mathematics, this concept forms the foundation for understanding more complex shapes and even three-dimensional objects.

To reinforce your understanding, try this exercise: Draw a rectangle on graph paper. Then, draw a diagonal to create two triangles. Count the squares to find the area of the rectangle, then compare it to the areas of the two triangles. You'll see that each triangle's area is indeed half of the rectangle's area!

As you continue to explore geometry, you'll find that this fundamental concept of a triangle's area being half of a rectangle's area with the same base and height is a powerful tool. It not only helps in calculating areas of triangles but also in understanding more complex shapes that can be broken down into triangles.

Remember, practice is key to mastering this concept. Try calculating areas of different triangles, and soon you'll find it becomes second nature. Whether you're studying for a math test, planning a home improvement project, or just satisfying your curiosity about the world around you, understanding the area of triangles is a valuable skill that opens doors to deeper mathematical insights.

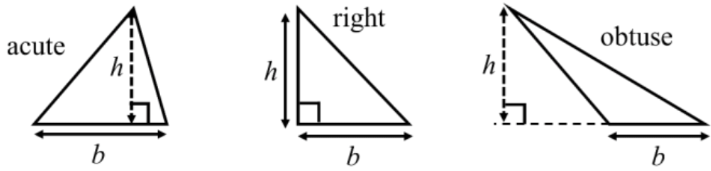
Calculating Area for Different Triangle Types

Calculating the area of triangles is a fundamental skill in geometry, and it's essential to understand how to apply this knowledge to different types of triangles. Whether you're dealing with a right triangle, acute triangle, or obtuse triangle, the basic formula for area remains the same: Area = (1/2) × base × height. However, the method for determining the height can vary depending on the triangle type. Let's explore how to calculate the area for each type of triangle using a step-by-step approach.

Right Triangles

Right triangles are perhaps the easiest to work with when calculating area. In a right triangle, one of the sides is always perpendicular to the base, making it the height.

1. Identify the base: Choose any side of the right triangle as the base.
2. Determine the height: The side perpendicular to the chosen base is the height.
3. Apply the formula: Area = (1/2) × base × height

Example: If a right triangle has a base of 6 cm and a height of 8 cm, the area would be (1/2) × 6 × 8 = 24 cm².

Acute Triangles

Acute triangles have all angles less than 90 degrees. To find the area of an acute triangle:

1. Choose any side as the base.
2. Draw a perpendicular line from the opposite vertex to the base (or its extension). This line is the height.
3. Measure or calculate the length of this perpendicular line.
4. Apply the area formula: Area = (1/2) × base × height

Example: For an acute triangle with a base of 10 cm and a height of 7 cm, the area would be (1/2) × 10 × 7 = 35 cm².

Obtuse Triangles

Obtuse triangles have one angle greater than 90 degrees. Calculating the area of an obtuse triangle requires careful consideration of the height:

1. Select the side opposite the obtuse angle as the base.
2. Draw a perpendicular line from the vertex of the obtuse angle to the base line extended. This perpendicular line is the height.
3. Measure or calculate the length of the perpendicular line.
4. Use the area formula: Area = (1/2) × base × height

Example: If an obtuse triangle has a base of 12 cm and a height of 5 cm, the area would be (1/2) × 12 × 5 = 30 cm².

Key Points to Remember

• The formula for area (1/2 × base × height) is consistent across all triangle types.
• The height must always be perpendicular to the base, regardless of triangle type.
• For right triangles, one side is always the height relative to the other as the base.
• In acute and obtuse triangles, you may need to extend the base line to find where the perpendicular height intersects.
• Practice identifying the base and height in various triangle orientations to improve your skills.

By understanding how to calculate the area for different types of triangles, you'll be well-equipped to solve a wide range of geometric problems. Remember that the key lies in correctly identifying the base and height for each specific triangle type. With practice, you'll become proficient in applying these concepts to various triangles, enhancing your overall mathematical skills and problem-solving abilities in geometry.

Practice Problems and Real-World Applications

To help students master the concepts of triangle area and perimeter, let's explore a set of practice problems for triangle area and their real-world applications. These exercises will reinforce understanding and demonstrate the practical importance of these geometric principles.

Practice Problem 1: Basic Calculation

Calculate the area and perimeter of a triangle with sides measuring 5 cm, 12 cm, and 13 cm.

Solution:

1. Perimeter = sum of all sides = 5 + 12 + 13 = 30 cm
2. For area, use Heron's formula: A = (s(s-a)(s-b)(s-c)), where s is the semi-perimeter
3. s = (5 + 12 + 13) / 2 = 15
4. A = (15(15-5)(15-12)(15-13)) = (15 * 10 * 3 * 2) = 900 = 30 cm²

Practice Problem 2: Word Problem

A triangular garden plot has sides of 8 m, 15 m, and 17 m. How much fencing is needed to enclose the garden, and what is the area available for planting?

Solution:

1. Fencing needed (perimeter) = 8 + 15 + 17 = 40 m
2. Area calculation using Heron's formula:
3. s = (8 + 15 + 17) / 2 = 20
4. A = (20(20-8)(20-15)(20-17)) = (20 * 12 * 5 * 3) = 3600 = 60 m²

Practice Problem 3: Architectural Application

An architect is designing a triangular skylight for a modern building. The skylight will have a base of 3 m and a height of 2 m. Calculate the area of glass needed and the length of framing required for the two equal sides.

Solution:

1. Area of glass = (base * height) / 2 = (3 * 2) / 2 = 3 m²
2. To find the length of the equal sides, use the Pythagorean theorem for triangles:
3. side² = (base/2)² + height² = 1.5² + 2² = 2.25 + 4 = 6.25
4. side = 6.25 2.5 m
5. Length of framing = 3 + 2.5 + 2.5 = 8 m

Real-World Applications

Understanding triangle area and perimeter is crucial in various fields:

• Architecture: Triangular elements are common in modern architecture, from skylights to roof designs. Architects use these calculations to determine material requirements and ensure structural integrity.
• Engineering: In civil engineering, triangular shapes are often used in bridge trusses and support structures. Accurate calculations of areas and perimeters are essential for load-bearing capacity and material efficiency.
• Design: Graphic designers and artists utilize triangular shapes in logos, layouts, and compositions. Understanding the geometry helps in creating balanced and visually appealing designs.
• Surveying: Land surveyors use triangulation methods to measure distances and areas of irregular land plots, often breaking them down into triangular sections.
• Construction: Builders and contractors frequently encounter triangular shapes in roof trusses, gables, and other structural elements. Knowing how to calculate the area and perimeter of these shapes is essential for accurate material estimation and construction planning.

Conclusion

In this lesson, we explored the fundamental concepts of triangle area formulas, focusing on perimeter and area calculations. We learned that the perimeter of a triangle is the sum of its three sides, while the area can be calculated using various formulas depending on the given information. The introduction video provided a visual understanding of these concepts, making them more accessible. Key formulas covered include A = (1/2)bh for area and P = a + b + c for perimeter. We also discussed special cases like equilateral and right triangles. Remember, practice is crucial for mastering these concepts. Try solving more problems to reinforce your understanding and explore real-world applications of triangles. This knowledge forms the foundation for more advanced geometric concepts and has practical uses in fields like architecture and engineering. Continue to challenge yourself and discover the fascinating world of triangle area formulas in mathematics and beyond.