Surface Area of Cylinders: Mastering Calculations and Applications Dive into the world of cylindrical geometry! Learn to calculate surface areas, understand key components, and apply your knowledge to real-world problems. Perfect for students seeking to excel in geometry.
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
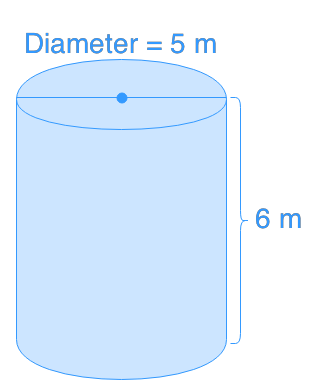
Introduction to Surface Area of Cylinders
The surface area of a cylinder, also known as a circular prism, is a fundamental concept in geometry. Our introduction video provides a crucial foundation for understanding this topic. A cylinder's surface area comprises two distinct parts: the circular bases at the top and bottom, and the rectangular lateral area wrapping around the sides. To calculate surface area accurately, you'll need to know two key components: the radius of the circular bases and the height of the cylinder. These measurements are essential for determining both the area of the circular ends and the rectangular side. By mastering the surface area of a cylinder, you'll gain valuable insights into three-dimensional shapes and their properties. This knowledge is applicable in various fields, from engineering and architecture to everyday problem-solving. As we delve deeper into this concept, you'll discover how these simple measurements can reveal much about a cylinder's characteristics and potential applications.
-
What is the formula for calculating the surface area of a cylinder?
The formula for calculating the surface area of a closed cylinder is SA = 2πr² + 2πrh, where r is the radius of the circular base and h is the height of the cylinder. This formula accounts for both the lateral area (2πrh) and the area of the two circular bases (2πr²).
-
How does the surface area formula differ for an open cylinder?
For an open cylinder (without one or both ends), the formula is adjusted. If one end is open, use SA = πr² + 2πrh. If both ends are open, the formula becomes SA = 2πrh, which only accounts for the lateral surface area.
-
Why is π (pi) used in the surface area formula for cylinders?
π is used because it's a fundamental constant in circular geometry. It appears in the formula for the area of a circle (πr²) and the circumference of a circle (2πr), both of which are essential components in calculating a cylinder's surface area.
-
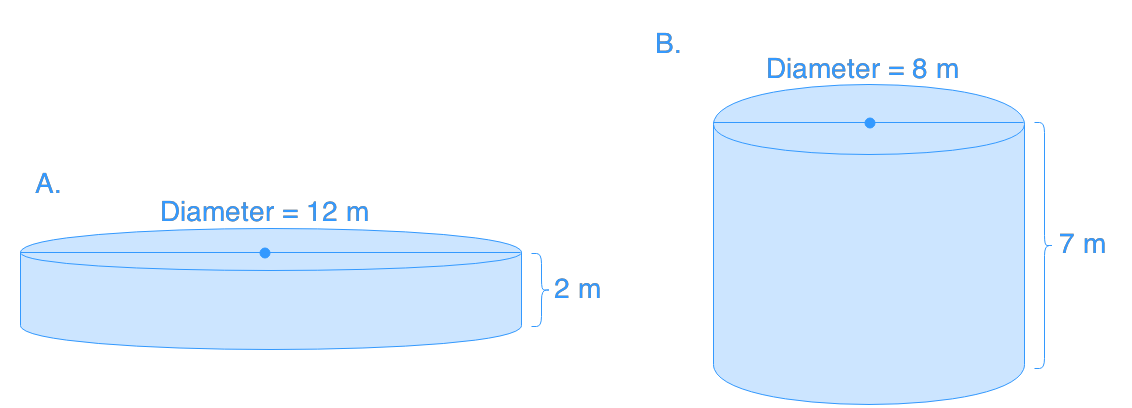
How does changing the radius affect the surface area of a cylinder compared to changing its height?
Changing the radius has a more significant impact on the surface area than changing the height. This is because the radius is squared in the formula (2πr²), while the height is not. A small increase in radius results in a larger increase in surface area compared to the same increase in height.
-
What are some real-world applications of calculating a cylinder's surface area?
Calculating a cylinder's surface area has numerous practical applications, including:
- Determining the amount of material needed to construct cylindrical tanks or containers
- Calculating the paint required to cover cylindrical structures
- Designing packaging for cylindrical products
- Estimating heat transfer rates in cylindrical pipes or vessels
- Calculating the surface area of cylindrical components in engineering and manufacturing
When delving into the fascinating world of geometry, particularly the surface area of cylinders, it's crucial to have a solid foundation in several key concepts. These prerequisite topics not only provide the necessary building blocks for understanding cylinders but also enhance your overall geometric intuition. Let's explore how these fundamental concepts intertwine with our main topic and why they're indispensable for mastering the surface area of cylinders.
First and foremost, a strong grasp of circles and circumference is essential. Cylinders are essentially three-dimensional extensions of circles, making this concept a cornerstone of our study. Understanding how to calculate the circumference of a circle is crucial because the lateral surface area of a cylinder is directly related to this measurement. When you unroll the curved surface of a cylinder, you're essentially working with a rectangle whose width is the circumference of the circular base. This connection between circles and cylinders highlights why mastering the circumference formula (2πr) is so vital.
Moreover, the concept of circumference plays a significant role in determining the amount of material needed to wrap around a cylindrical object or in calculating the distance traveled by a rolling cylinder. By solidifying your knowledge of circles and their properties, you're setting the stage for a deeper understanding of cylindrical surfaces and their areas.
Another critical prerequisite topic is the arc length and surface area of parametric equations. While this might seem advanced, it provides invaluable insights into how surfaces can be described mathematically, especially curved surfaces like those found in cylinders. The concept of lateral surface area, which is central to calculating a cylinder's surface area, is deeply rooted in these parametric representations.
Understanding how to work with parametric equations allows you to visualize and compute the surface area of more complex cylindrical shapes, such as elliptical cylinders or cylinders with varying radii. This knowledge becomes particularly useful when dealing with real-world applications or advanced geometric problems involving cylinders. The ability to break down a cylinder's surface into manageable sections using parametric equations is a powerful tool in your geometric arsenal.
Equally important is an introduction to surface area of 3-dimensional shapes. This foundational knowledge serves as a bridge between flat, two-dimensional geometry and the more complex world of three-dimensional objects. Cylinders, being 3D shapes, require a shift in thinking from area to surface area. Understanding how to visualize and mentally manipulate three-dimensional shapes is crucial for accurately calculating their surface areas.
This prerequisite topic helps you develop the spatial reasoning skills necessary to break down a cylinder into its component parts - the circular bases and the curved lateral surface. It teaches you to think about surface area as the sum of all exposed surfaces, a concept that's directly applicable to cylinders. By practicing with various 3D shapes, you'll enhance your ability to see the 'unfolded' version of a cylinder, making the calculation of its surface area more intuitive.
The importance of these prerequisite topics cannot be overstated when it comes to mastering the surface area of cylinders. They provide the conceptual framework and mathematical tools necessary to approach cylindrical problems with confidence. For instance, when calculating the surface area of a cylinder, you'll need to combine your knowledge of circular area (for the bases) with the concept of rectangular area (for the unrolled lateral surface). This synthesis of ideas is only possible with a solid understanding of the prerequisite topics.
Furthermore, these foundational concepts extend beyond just cylinders. They form the basis for understanding more complex shapes and geometrical concepts. The skills you develop in visualizing three-dimensional shapes, working with curved surfaces, and applying circular properties will serve you well in various areas of mathematics and real-world applications.
In conclusion, approaching the study of cylinder surface area without a firm grasp of these prerequisite topics would be like trying to build a house without a foundation. Each concept - from circles and circumference to parametric equations and 3D shape visualization - contributes uniquely to your understanding of