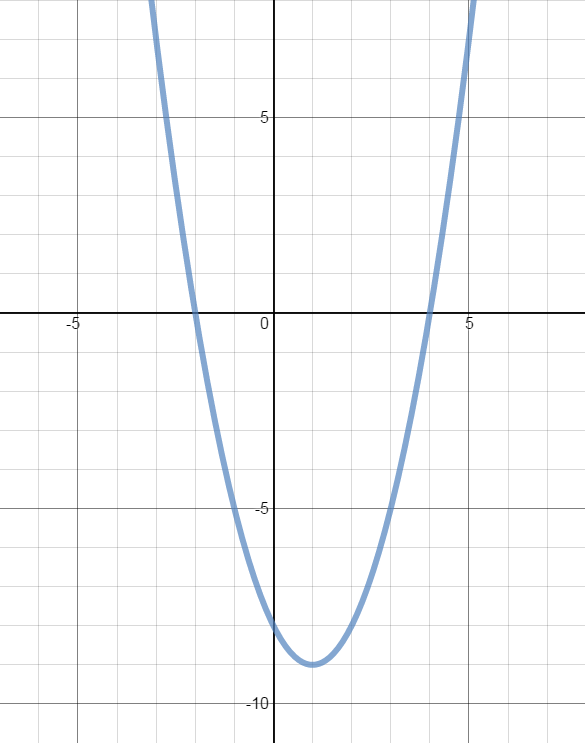
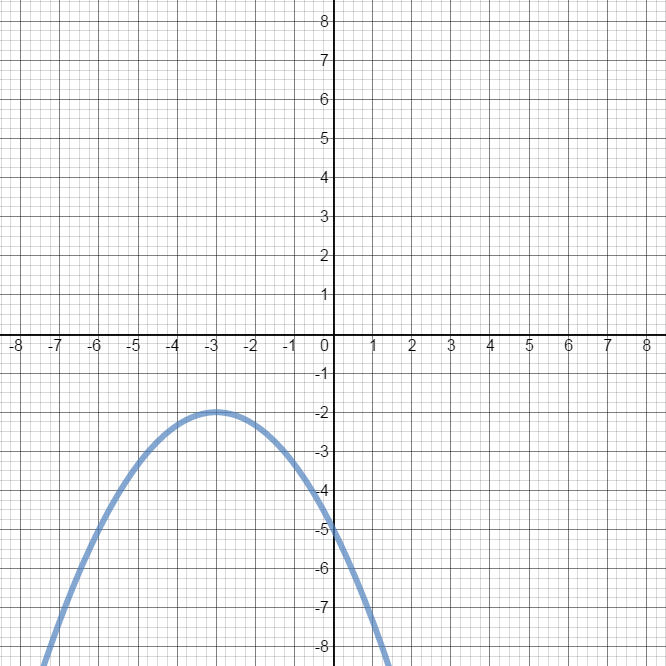
Three properties that are universal to all quadratic functions: 1) The graph of a quadratic function is always a parabola that either opens upward or downward (end behavior); 2) The domain of a quadratic function is all real numbers; and 3) The vertex is the lowest point when the parabola opens upwards; while the vertex is the highest point when the parabola opens downward.
Characteristics of quadratic functions
Get the most by viewing this topic in your current grade. Pick your course now.
Examples
- Determining the Characteristics of a Quadratic Function Using Various Methods
Determine the following characteristics of the quadratic function :
• Opening of the graph
• intercept
• intercept(s)
• Vertex
• Axis of symmetry
• Domain
• Range
• Minimum/Maximum value
- From the graph of the parabola, determine the:
• vertex
• axis of symmetry
• y-intercept
• x-intercepts
• domain
• range
• minimum/maximum value
- Identifying Characteristics of Quadratic function in General Form:
is a quadratic function in general form.
i) Determine:
• y-intercept
• x-intercepts
• vertex
ii) Sketch the graph. - Identifying Characteristics of Quadratic Functions in Vertex Form:
is a quadratic function in vertex form.
i) Determine:
• y-intercept
• x-intercepts
• vertex
ii) Sketch the graph.