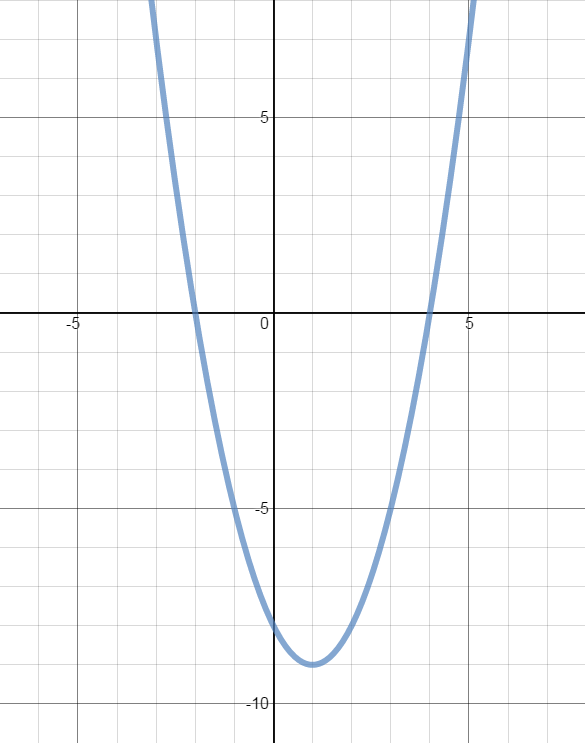
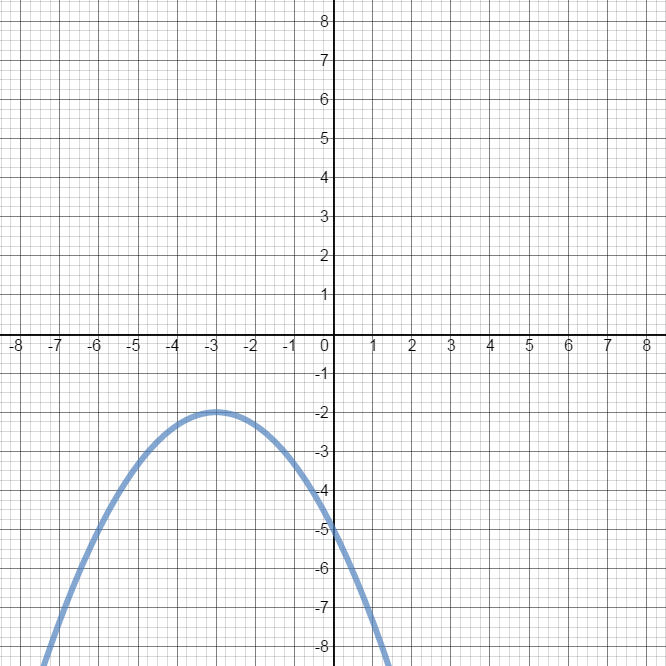
Three properties that are universal to all quadratic functions: 1) The graph of a quadratic function is always a parabola that either opens upward or downward (end behavior); 2) The domain of a quadratic function is all real numbers; and 3) The vertex is the lowest point when the parabola opens upwards; while the vertex is the highest point when the parabola opens downward.
Examples
0/10 watched
- Determining the Characteristics of a Quadratic Function Using Various Methods
Determine the following characteristics of the quadratic function :
• Opening of the graph
• intercept
• intercept(s)
• Vertex
• Axis of symmetry
• Domain
• Range
• Minimum/Maximum value
- From the graph of the parabola, determine the:
• vertex
• axis of symmetry
• y-intercept
• x-intercepts
• domain
• range
• minimum/maximum value
- Identifying Characteristics of Quadratic function in General Form:
is a quadratic function in general form.
i) Determine:
• y-intercept
• x-intercepts
• vertex
ii) Sketch the graph. - Identifying Characteristics of Quadratic Functions in Vertex Form:
is a quadratic function in vertex form.
i) Determine:
• y-intercept
• x-intercepts
• vertex
ii) Sketch the graph.