One to one functions - Relations and Functions
One to one functions
Basic concepts:
- Inverse functions
Related concepts:
- Difference quotient: applications of functions
Lessons
Notes:
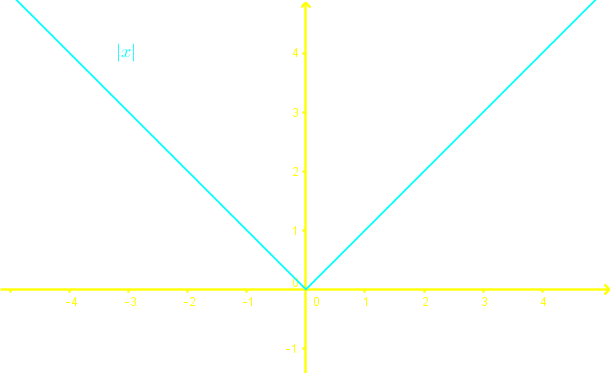
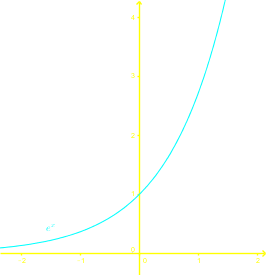
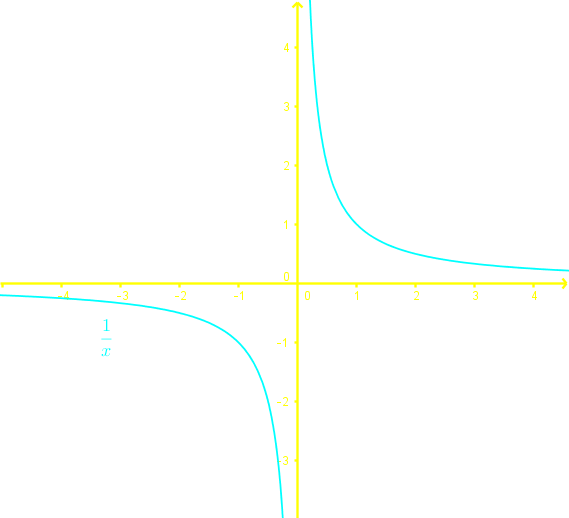
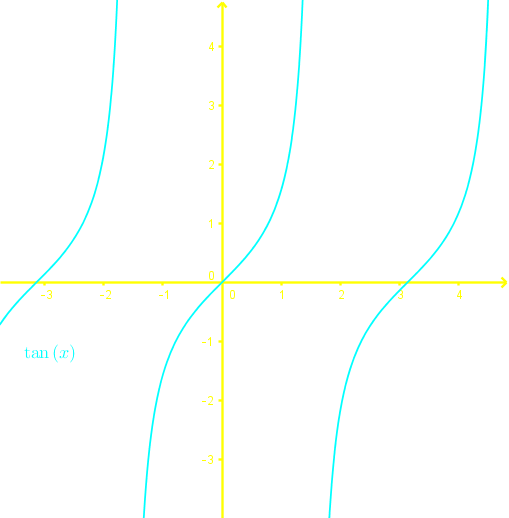
To determine if an expression is a function, we perform the vertical line test.
Surjective/Onto: For every value, there exists at least one value.
Injective/Into/one-to-one: For every value, there exists at most one value.
To determine if a function is one-to-one, we perform the horizontal line test.
