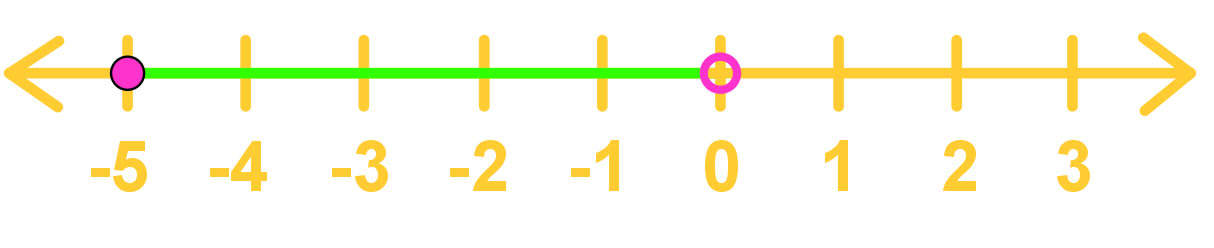
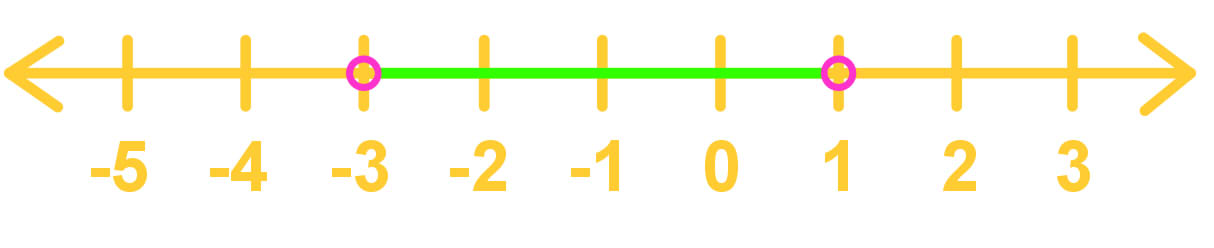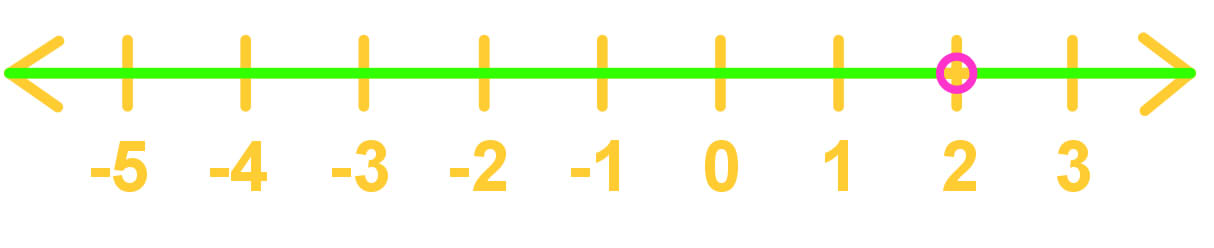A set is a collection of elements (usually numbers)
E.g. { > 0} should be read as "the set of all x's that are an element of the real numbers such that x is greater than 0."
Special symbols:
- = real numbers
- = integers
- = natural numbers
- = rational numbers
- = complex numbers
- = imaginary numbers