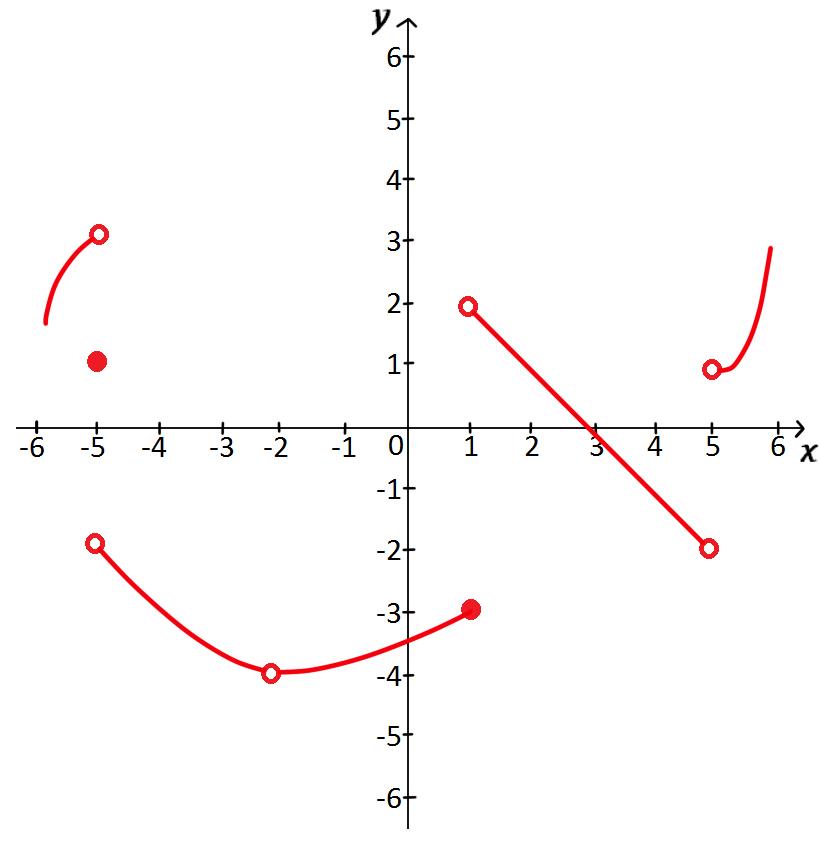
Limit is an important instrument that helps us understand ideas in the realm of Calculus. In this section, we will learn how to find the limit of a function graphically using one-sided limits and two-sided limits.
DEFINITION:
left-hand limit:
We say "the limit of f(x), as x approaches a from the negative direction, equals L".
It means that the value of f(x) becomes closer and closer to L as x approaches a from the left, but x is not equal to a.
DEFINITION:
right-hand limit:
We say "the limit of f(x), as x approaches a from the positive direction, equals L".
It means that the value of f(x) becomes closer and closer to L as x approaches a from the right, but x is not equal to a.
DEFINITION:
if and only if and
left-hand limit:
We say "the limit of f(x), as x approaches a from the negative direction, equals L".
It means that the value of f(x) becomes closer and closer to L as x approaches a from the left, but x is not equal to a.
DEFINITION:
right-hand limit:
We say "the limit of f(x), as x approaches a from the positive direction, equals L".
It means that the value of f(x) becomes closer and closer to L as x approaches a from the right, but x is not equal to a.
DEFINITION:
if and only if and