Subtracting Mixed Fractions: A Comprehensive Tutorial Unlock the secrets of subtracting mixed fractions with our step-by-step guide. Learn essential techniques, avoid common pitfalls, and boost your math confidence through practice and examples.
- Simplify fractions: Method A - By using greatest common factors
- Simplify fractions: Method B - By using common factors
- What are equivalent fractions?
- How to add fractions?
- How to subtract frations?
• subtracting with improper fractions
• subtracting with mixed numbers - Proper fractions VS. Improper fractions VS. Mixed fractions
- Subtract or add using the given diagram.
- Subtract or add.
- Maren goes to soccer practice for 254 hour each day. In the morning, she has 143 hour of practice. How many hours of practice does she have in the afternoon?
- Hannah ran for 141 hour and then biked for 132 hour. For how long did she exercise?
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction
Welcome to our lesson on subtracting mixed fractions, a crucial skill in mathematics. To begin, we'll explore an introduction video that provides a visual foundation for understanding this concept. This video is essential as it demonstrates the process step-by-step, making it easier to grasp the fundamentals. Throughout this lesson, we'll delve into the intricacies of subtracting mixed fractions, which involves working with numbers that combine whole numbers and fractions. We'll cover various scenarios, including cases where you need to convert mixed numbers to improper fractions before performing the subtraction. This conversion is sometimes necessary to simplify the process and avoid errors. By mastering these techniques, you'll be able to confidently approach problems involving mixed fractions in both academic and real-world contexts. Remember, practice is key to becoming proficient in subtracting mixed fractions, so be sure to work through the examples and exercises provided.
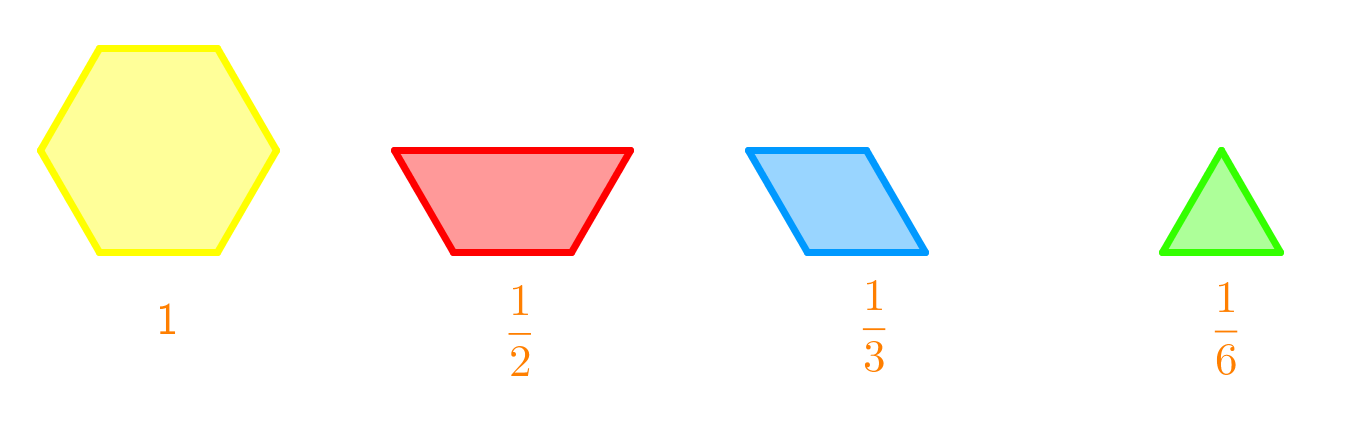
Subtract or add using the given diagram.


Step 1: Identify the Shapes and Their Values
First, examine the given diagram. Notice the different shapes and their corresponding values. The yellow shape represents the whole number 1. The blue shapes each represent one-third (1/3), and there are two of them. The green triangles each represent one-sixth (1/6), and there are three of them.
Step 2: Convert Shapes to Fractions
Next, convert the shapes into fractions. The yellow shape is 1. The two blue shapes are each 1/3, so together they make 1/3 + 1/3 = 2/3. The three green triangles are each 1/6, so together they make 1/6 + 1/6 + 1/6 = 3/6.
Step 3: Combine the Fractions
Now, combine the fractions. Start with the whole number 1. Add the two blue shapes (2/3) to it. This gives you 1 + 2/3. Then, add the three green triangles (3/6) to this sum. So, you have 1 + 2/3 + 3/6.
Step 4: Find a Common Denominator
To add these fractions, you need a common denominator. The denominators are 3 and 6. The least common multiple of 3 and 6 is 6. Convert 2/3 to a fraction with a denominator of 6. Multiply both the numerator and the denominator by 2: 2/3 = 4/6. Now, you have 1 + 4/6 + 3/6.
Step 5: Add the Fractions
Now, add the fractions with the common denominator. Combine 4/6 and 3/6: 4/6 + 3/6 = 7/6. So, you have 1 + 7/6.
Step 6: Simplify the Fraction
Notice that 7/6 is an improper fraction. Convert it to a mixed number. 7/6 is the same as 1 + 1/6. So, you have 1 + 1 + 1/6, which simplifies to 2 + 1/6.
Step 7: Final Answer
Combine the whole numbers and the fraction to get the final answer. The result is 2 and 1/6.
Here are some frequently asked questions about subtracting mixed fractions:
1. How do you subtract mixed fractions step by step?
To subtract mixed fractions, follow these steps: 1. Convert mixed fractions to improper fractions. 2. Find a common denominator if needed. 3. Subtract the numerators while keeping the common denominator. 4. Simplify the result and convert back to a mixed fraction if necessary.
2. How do you borrow when subtracting mixed fractions?
When borrowing is needed: 1. Take 1 from the whole number part. 2. Convert this 1 to a fraction with the same denominator as the fractional part. 3. Add this to the existing fraction. 4. Proceed with the subtraction using the new mixed fraction.
3. How do you subtract mixed fractions using improper fractions?
To subtract using improper fractions: 1. Convert both mixed fractions to improper fractions. 2. Find a common denominator if needed. 3. Subtract the numerators while keeping the common denominator. 4. Simplify the result and convert back to a mixed fraction if desired.
4. How do you subtract mixed fractions with like denominators?
For mixed fractions with like denominators: 1. Subtract the whole numbers. 2. Subtract the fractions. 3. If borrowing is needed, take 1 from the whole number and add it to the fraction before subtracting. 4. Simplify the result if possible.
5. What are common mistakes when subtracting mixed fractions?
Common mistakes include: - Forgetting to find a common denominator for unlike denominators. - Incorrectly borrowing when needed. - Subtracting denominators instead of just numerators. - Forgetting to simplify the final answer. - Incorrectly converting between mixed and improper fractions.
Understanding the foundation of mathematics is crucial when tackling more complex concepts like adding and subtracting mixed numbers. To excel in this area, it's essential to grasp several key prerequisite topics that form the building blocks of this skill.
One fundamental concept to master is the negative exponent rule. While it may seem unrelated at first, understanding how to work with whole numbers and proper fractions is vital when dealing with mixed numbers. This knowledge helps in breaking down mixed numbers into their whole number and fractional components, making addition and subtraction more manageable.
Another critical skill is multiplying improper fractions and mixed numbers. This topic is particularly relevant because it involves simplifying improper fractions, a process often required when adding or subtracting mixed numbers. Being proficient in this area allows for smoother conversions between improper fractions and mixed numbers during calculations.
Perhaps the most directly related prerequisite is subtracting fractions with like denominators. This skill forms the core of subtracting mixed numbers, as you'll often need to perform this operation on the fractional parts. Mastering this concept ensures accuracy and efficiency when working with more complex mixed number problems.
Understanding greatest common factors (GCF) is also crucial. When adding or subtracting mixed numbers, you may need to simplify fractions or find a common denominator. Knowledge of GCF helps in identifying the least common multiple of denominators, which is essential for these operations.
Speaking of common denominators, proficiency in finding the least common multiple (LCM) is indispensable. This skill is particularly useful when adding or subtracting mixed numbers with different denominators. Understanding prime factorization for LCM allows you to quickly determine the common denominator needed for these operations.
By mastering these prerequisite topics, you'll build a strong foundation for adding and subtracting mixed numbers. Each concept contributes to your overall understanding and ability to perform these operations accurately and efficiently. Remember, mathematics is a cumulative subject, and investing time in these fundamental skills will pay dividends as you progress to more advanced topics. So, take the time to review and practice these prerequisites your future self will thank you when tackling complex mixed number problems becomes second nature!




