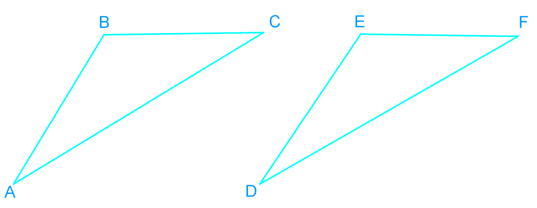
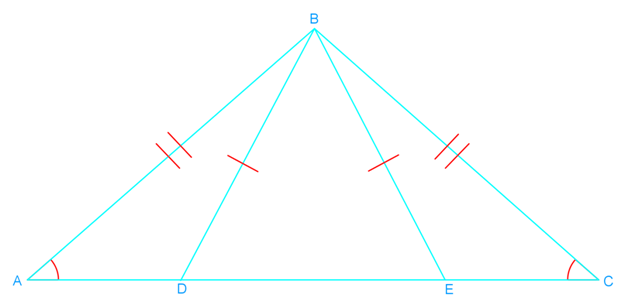
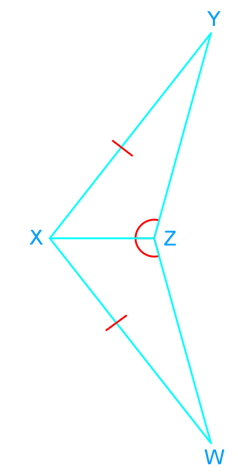
Introduction to Proving Triangles Congruent: ASA and AAS Proofs
Understanding how to prove triangles congruent is a fundamental skill in geometry. Two essential methods for proving triangles congruent are the Angle-Side-Angle (ASA) and Angle-Angle-Side (AAS) proofs. Our introduction video provides a comprehensive overview of these concepts, serving as a crucial foundation for mastering triangle congruency. The ASA proof requires two angles and the included side to be congruent, while the AAS proof needs two angles and a non-included side to be congruent. It's vital to distinguish between congruency and similarity in triangles; congruent triangles are identical in shape and size, whereas similar triangles share the same shape but may differ in size. By grasping these proofs, students can develop their logical reasoning skills and apply them to more complex geometric problems. The video demonstrates step-by-step processes for both ASA and AAS proofs, ensuring a solid understanding of these essential congruent triangles concepts.