Sign In
Sign Up
flag-uk

Pythagorean identities

  1. Examples0/5 watched
  2. Practice0/9 practiced
  1. 0/5
  2. 0/9
Now Playing:Pythagorean identities– Example 1
Examples
0/5 watched
  1. Use the unit circle to derive the Pythagorean Identity:
    cos2θ+^2 \theta + sin2θ=1^2 \theta = 1

    0/1

    Practice
    0/9
    Pythagorean Identities 1
    Quotient identities and reciprocal identities
    Jump to:NotesPrerequisitesRelated
    Notes
    Pythagorean identities are formulas, derived from Pythagorean Theorem, that allow us to find out where a point is on the unit circle. Learn the tricks and tips on how to use the unit circle to derive and prove the Pythagorean identities can be difficult.

    What are the Pythagorean identities?

    An identity in mathematics is an equation that is always true. The Pythagorean identities all involve the number 1 and its Pythagorean aspects can be clearly seen when proving the theorems on a unit circle.

    Pythagorean identities

    We are going to explore the Pythagorean identities in this question. You may refer to the below formula sheet when dealing with the 3 Pythagorean identities.

    Pythagorean identities
    the list of Pythagorean identities

    Let's explore the Pythagorean identities. The first of these three states that sine squared plus cosine squared equals one. The second one states that tangent squared plus one equals secant squared. For the last one, it states that one plus cotangent squared equals cosecant squared.

    In the following question, we're going to try to use a unit circle to prove the first Pythagorean identity: sine squared plus cosine squared equals one.

    Pythagorean identities examples

    Question:

    Use the unit circle to derive the Pythagorean Identity: cos⁡2θ+sin⁡2θ=1\cos^2 \theta + \sin^2 \theta = 1

    How do we begin? Do you remember the properties of a unit circle? We've covered the unit circle in the previous section. To quickly recap, a unit circle is just a circle with radius of one unit, i.e. the radius must equal one.

    use the unit circle to derive the Pythagorean identity
    derive Pythagorean identity using unit circle

    Refer to the above image. We'll identify a point on the circle at X,Y. Here, the X coordinate is X and the Y coordinate is Y.

    From this point, let's draw a perpendicular line to the X axis. We will be focusing on this triangle.

    In the above image, take a moment to recall what ? means. It's actually the reference angle, correct? It is one of the most important angles in trigonometry.

    In the reference angle, what does it mean if the X coordinate equals X? It means that the length of the X segment is X. In a similar sense, if the Y coordinate is Y, that means the length of the vertical segment of the triangle would be Y.

    Let's demonstrate this with actual numbers to illustrate that concept.

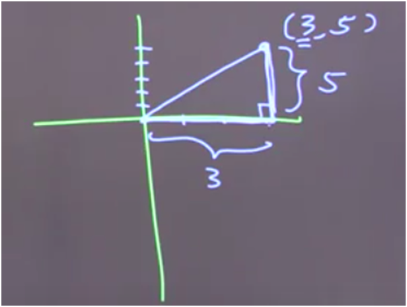
    example of x, y coordinates and length of segments fn a triangle
    illustration of relationship between coordinate and length of segments of a triangle

    In the above example, there's a point called 3,5. If we draw a triangle, the 3 depicts the X coordinate. This means that the length of this segment is 3. Now, if the Y coordinate is 5, what does that mean? The length of the vertical segment in the triangle must be five.

    Going back to the previous unit circle illustration, let's focus on the right-angled triangle and apply the Pythagoras theorem. What is the Pythagoras theorem? The Pythagoras tells us that X squared plus Y squared equals to the hypotenuse squared. The hypotenuse in this case is one, since we're using a unit circle. So here we have X squared plus Y squared equals one squared.

    One neat thing about the unit circle is that its X coordinate can also be represented in terms of the angle theta. The X coordinate can be represented as cosine theta, while its Y coordinate can be represented as sine theta. Keep in mind that this is only for a unit circle. So for any point on the unit circle: the X coordinate can be represented as cosine theta; the Y coordinate can be represented as sine theta.

    derive the other two pythagorean identities using first pythagorean identity
    derive the other Pythagorean identities from cos⁡2θ+sin⁡2θ=1\cos^2 \theta + \sin^2 \theta = 1

    Through using the unit circle, the answer becomes very obvious. One squared is just one. The X coordinate can also be represented as cosine theta. The Y coordinate can be represented as sine theta. And voila! We are done. From the unit circle, we've successfully proved that cosine squared plus sine squared equals one, tackling one out of 3 Pythagorean identities.

    Download the Trigonometry identities chart here