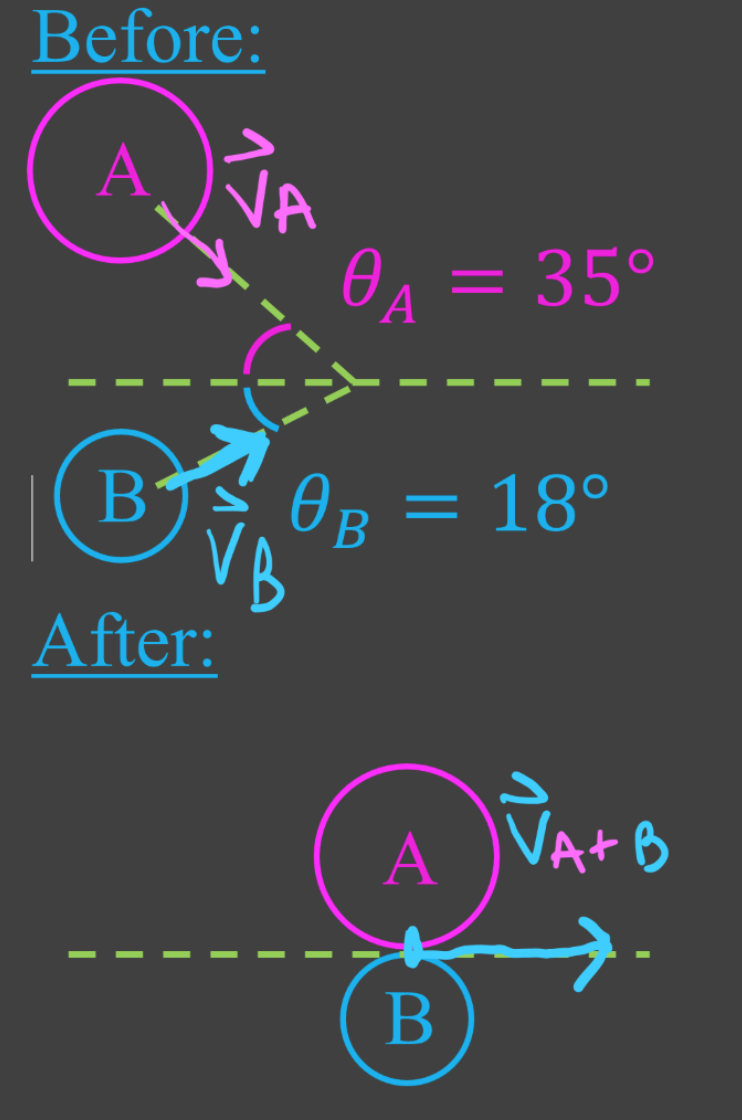1. Home
  2. >A-Level Maths
  3. >Momentum
Help

Conservation of momentum in two dimensions

All You Need in One Place

Everything you need for better marks in primary, GCSE, and A-level classes.

Learn with Confidence

We’ve mastered the UK’s national curriculum so you can study with confidence.

Instant and Unlimited Help

24/7 access to the best tips, walkthroughs, and practice questions.

0/1
?
Intros
Lessons

  1. Introduction to conservation of momentum in two dimensions

    • Review of conservation of momentum
    • Vector nature of momentum and conservation of momentum
0/8
?
Examples
Lessons
  1. ∑p⃗i=∑p⃗f:\bold{\sum\vec{p}_i = \sum\vec{p}_f}: Objects that bounce apart after collision in two dimensions
    1. 1.25 kg ball A is moving at 3.40 m/s [E] when it strikes stationary 1.00 kg ball B. After the collision, ball A moves off at an angle of [60.0° N of E], and ball B moves off at an angle of [30.0° S of E]. Find the velocities of A and B after collision.
      before and after of balls A and B collision
    2. 1.10 kg puck A travelling at 2.00 m/s [E] collides with 0.860 kg puck B moving 0.400 m/s [W]. After the collision, puck A moves off at 1.60 m/s [40.0° N of E]. Find the velocity of puck B.
      before and after of objects that bounce apart after collision example b
  2. ∑p⃗i=∑p⃗f:\bold{\sum\vec{p}_i = \sum\vec{p}_f}: Objects that stick together after collision in two dimensions
    1. 1100.0 kg car A travelling at 12.0 m/s [E] collides with 975 kg car B travelling 19.0 m/s [N]. The cars stick together. Find the velocity of the two vehicles after collision.
    2. 0.50 kg magnetic puck A travelling at 1.1 m/s collides with 0.35 kg puck B travelling with an unknown velocity, as shown in the diagram. The two pucks stick together and travel due [E]. Find the initial velocity of the second puck. before and after of pucks sticky collision
  3. ∑p⃗i=∑p⃗f:\bold{\sum\vec{p}_i = \sum\vec{p}_f}: Objects that explode apart in two dimensions
    1. A bomb initially at rest explodes, sending three fragments in different directions as shown in the diagram. Find the velocity of the 0.71 kg fragment.
      bomb explosion fragments

    2. A 21.0 kg child holding a 0.755 kg snowball rides a 3.00 kg sled on a frictionless ice surface at 2.50 m/s [E]. The child throws the snowball, giving it an impulse due [N] relative to the sled. The snowball travels at 6.00 m/s immediately after it is thrown.

    3. Balls A, B, and C roll together as shown in the diagram, with all three balls colliding at the same time. Find the mass of ball C if the 3 balls are stationary after colliding.
      balls A, B, and C collision
    4. A spacecraft with a total mass of 8620 kg is travelling through space at a speed of 156 m/s. Control wants to adjust its direction by 25.0°, and increase its speed to 175 m/s. Gas is ejected though a thruster on the side of the craft, travelling at 85.0° clockwise from the craft's original direction of motion. Find the mass of gas ejected.
      spacecraft thrusting
Topic Notes
?

In this lesson, we will learn:

  • Review of conservation of momentum
  • Vector nature of momentum and conservation of momentum
  • Problem solving with conservation of momentum in two dimensions

Notes:

  • Momentum is a conserved quantity and a vector.
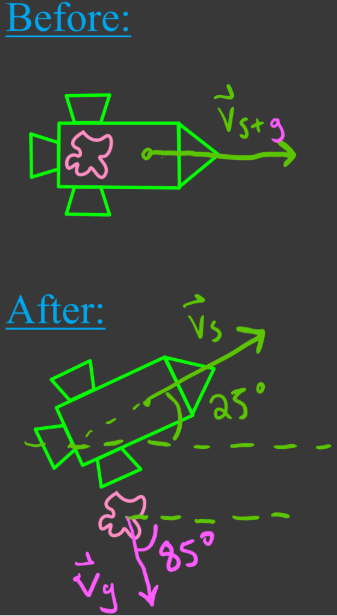
    • In a collision between a set of objects, total momentum of the objects before collision = total momentum after collision.
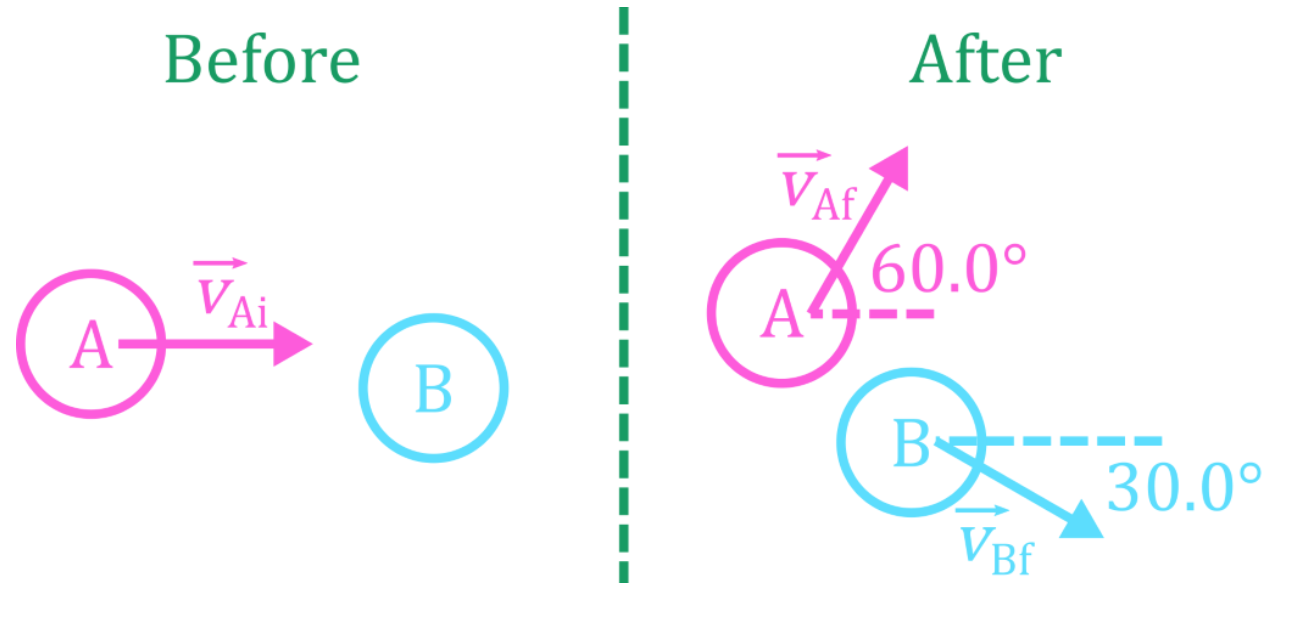
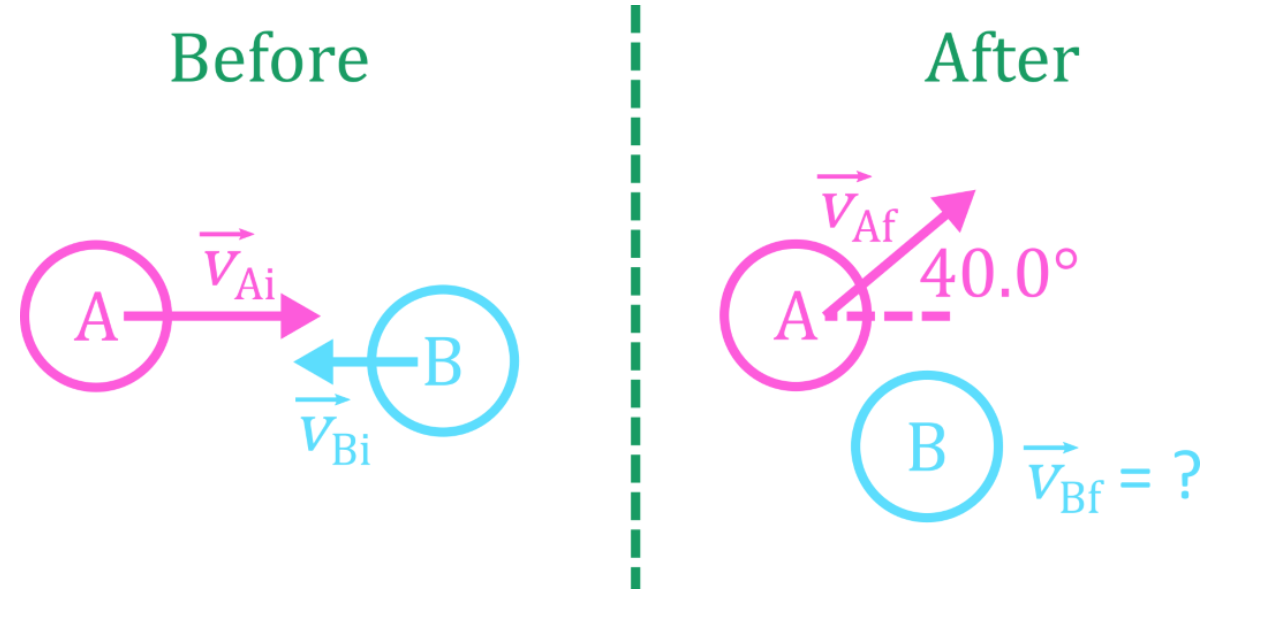
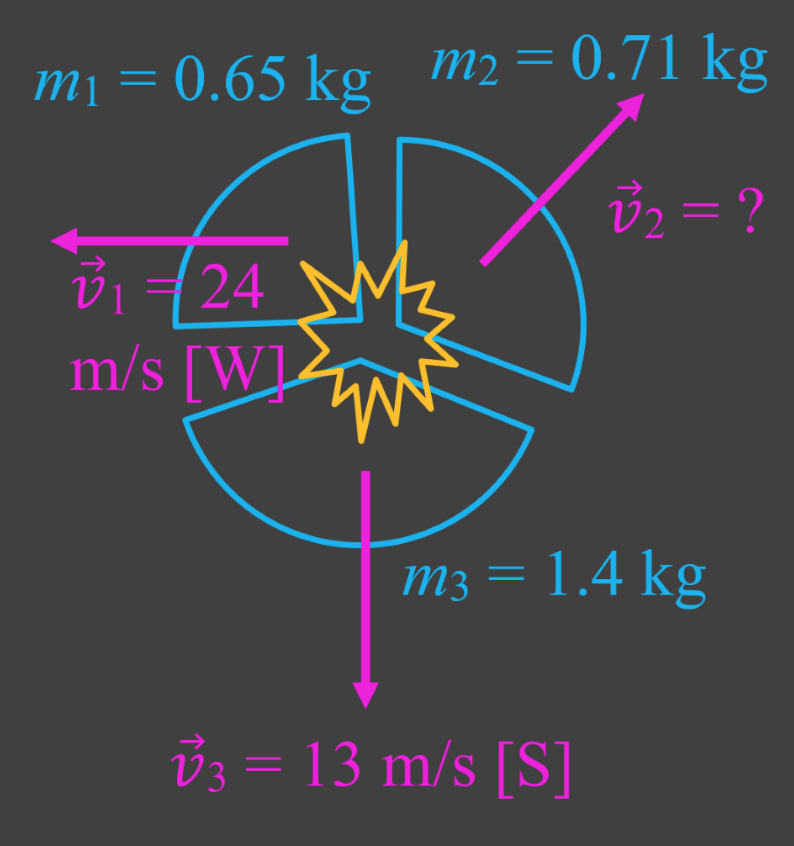
    • When using conservation of momentum on objects that move in two dimensions, use vector addition (tip-to-tail method).

Momentum

p⃗=mv⃗:\vec{p} = m \vec{v}: momentum, in kilogram meters per second (kg∙m/s)

m:m: mass, in kilograms (kg)

v⃗:\vec{v}: velocity, in meters per second (m/s)


Impulse

J⃗=F⃗Δt=Δp⃗=mΔv⃗\vec{J} = \vec{F} \Delta t = \Delta \vec{p} = m\Delta \vec{v}

J⃗:\vec{J}: impulse, in newton seconds (N∙s)

F⃗:\vec{F}: force, in newtons (N)

t⃗:\vec{t}: time, in seconds (s)


Conservation of Momentum

∑p⃗i=∑p⃗f\sum\vec{p}_i = \sum\vec{p}_f

p⃗i:\vec{p}_i: initial momentum, in kilogram meters per second (kg·m/s)

p⃗f:\vec{p}_f: final momentum, in kilogram meters per second (kg·m/s)


Law of Sines

asinA=bsinB=cSinC\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{SinC}
a,b,c: length of sides a,b,c
A,B,C: angles opposite sides a, b, c

Law of Cosines

c2=a2+b2−2ab cosCc^2 = a^2 + b^2 - 2ab \,cosC