Formula for circumference
What exactly is the circumference of a circle? It's actually defined as the length of the edge surrounding a circle, that is, the perimeter of a circle. We need to use to help us find the circumference. The formula for finding the circumference includes the diameter, and looks like this:
C = d
To make this easier, we can also find the circumference if we know the radius of a circle. We know that the diameter is equalled to 2r (2 times the radius), so in other words, the formula for a circle's circumference is:
C = 2r
Either of these circumference formulas can be used to help you solve problems.
How to find the circumference of a circle
We'll do a three examples to help you learn how to find the circumference of a circle using the formulas we just learned.
Question:
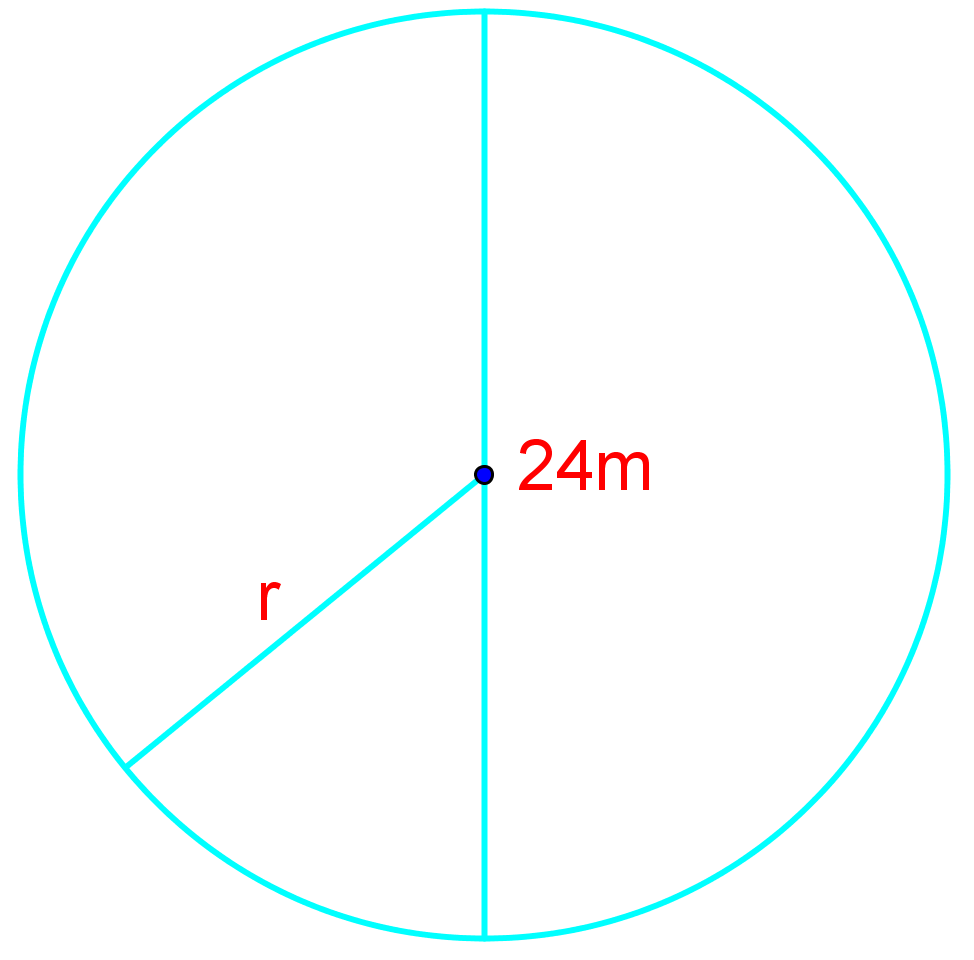
Find the circumference of the following circle:
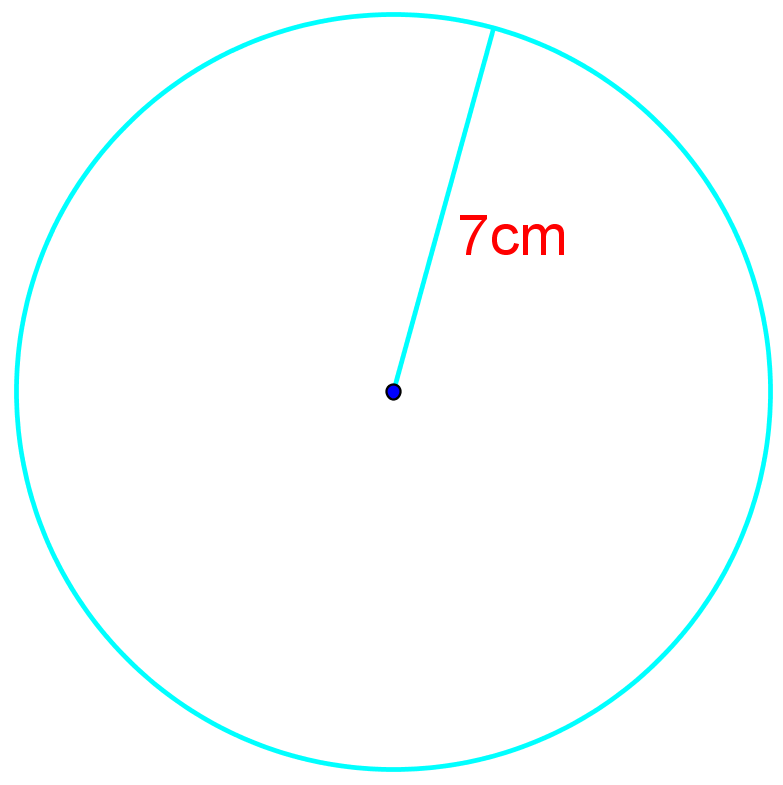
Solution:
C = 2r
C = 2(7)
C = 43.98cm
In this example, we are given a circle, with only one of its characteristics given to us. The 7cm is the measurement of the line from the center of the circle to its edge, which is, in other words, the radius of the circle. Luckily, we have a circumference formula to help us out when we know the radius: C = 2r. Simply by substituting in r with 7, we're able to find that the circumference is 43.98cm.
Question:
Find the circumference of the following circle:

Solution:
C = 2r
C = 2(8½)
C = 53.41m
Once again in this example, we're given the radius of the circle. Although it's not a clean number like our previous example, but we can still simply plug the number directly into the formula like what we did above. Be aware of the units that this circle's radius is given in and remember to give your final answer in the same unit. In this question, we find that the circumference is equalled to 53.41m.
Question:
Find the circumference of the following circle:
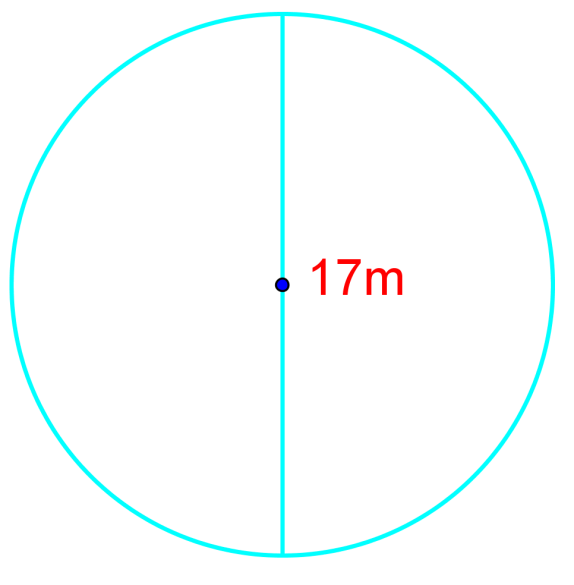
Solution:
C = d
C = (17)
C = 53.41m
In this example, we aren't given the radius. We're given the distance across a circle through its center, which is also called the diameter of a circle. Again, referring back to the two equations we can use to calculate a circle's circumference, we find that one of them simply uses C = d. When we substitute "d" with 17, we find that we'll get the answer of 53.41m.
An interesting point to note is that you can still use the other formula for finding the circumference that uses the radius. All we have to do is first change the diameter into a radius. We know that the diameter is 2 times the radius, so therefore, we can divide 17 by 2 to find the radius of 8.5 You can see that this number is actually the same one as the radius given in the previous circle, and therefore, we get the same answer when we use the C = 2r formula.
Generally, it's easier to use whichever formula corresponds with the characteristics of the circle you are given. However, if you're unable to remember both of the formulas, you can always manipulate the info you're given so that it fits into the formula you do remember.
Feel free to play around with this online circle calculator to see how the circumference changes as the diameter and radius changes.