Sign In
Sign Up
flag-uk

Change in Variables: Transform and Simplify Complex Calculus
Unlock the power of variable transformation in calculus. Learn to simplify intricate integrals, master coordinate systems, and solve real-world problems with confidence. Elevate your mathematical skills today!

  1. Intros0/3 watched
  2. Examples0/6 watched
  1. 0/3
  2. 0/6
Now Playing:Change in variables – Example 0a
Intros
0/3 watched
  1. Change in Variables Overview:
  2. Change in Variables Overview:
    Transformations
    • Transformation = change one variable to another
    • Similar to u-substitution in integral calculus
    • xyxy-coordinate →\to uvuv-coordinate
    • An Example of Change in Variable of Regions
  3. Change in Variables Overview:
    Jacobian of a Transformation
    • Definition of Jacobian
    • Determinant of a 2 x 2 matrix
    • Deals with derivatives
Examples
0/6 watched
  1. Finding the Transformations
    Suppose we have  R\, R, where  R \, R \, is the region bounded by  y=x+2,y=−x\, y = x + 2, y = -x , and  y=x2\, y = \frac{x}{2} . Use the transformation  x=13u−13v  \, x = \frac{1}{3}u - \frac{1}{3}v \, and  y=13u+13v  \, y = \frac{1}{3}u + \frac{1}{3}v \, to determine the new region.
    Change in variables
    Jump to:NotesConceptFAQsPrerequisites
    Notes
    Notes:

    Transformations

    Recall that in Integral Calculus, we can change the variable xx to uu of an integral using u-substitution. In other words, we can change from

    ∫f(x)dx→∫f(u)du \int f(x)dx \to \int f(u)du

    We would like to do something similar like this with double integrals.

    Transformations is about changing from one variable to another. We will first start by transforming regions.


    Jacobian of a Transformation

    The Jacobian of a transformation x=g(u,v)x=g(u,v) & y=h(u,v)y=h(u,v) is the following:

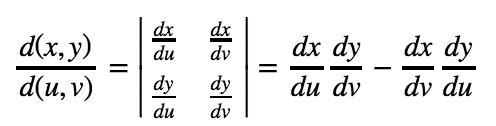
    jacobian of a transformation

    It is the determinant of a 2 x 2 matrix.

    Change of Variables for a Double Integral

    Suppose we want to integrate the function f(x,y)f(x,y) in the region RR under the transformation x=g(u,v)x=g(u,v) & y=h(u,v)y=h(u,v). Then the integral will now become:

    ∫∫Rf(x,y)dA=∫∫Sf(g(u,v),h(u,v))∣d(x,y)d(u,v)∣dudv\int \int_R f(x,y)dA = \int \int_S f(g(u,v), h(u,v)) \left| \frac{d(x,y)}{d(u,v)}\right| du dv

    Concept

    Introduction to Change in Variables

    Change in variables, a fundamental concept in calculus, is a powerful technique for simplifying complex integrals and solving multivariable problems. This transformation method builds upon the U-substitution learned in Calculus 2, extending its application to higher dimensions in Calculus 3. The introductory video provides a crucial foundation for understanding this topic, demonstrating how to rewrite integrals in terms of new variables. By mastering change in variables, students can tackle more advanced problems in multivariable calculus, such as converting between coordinate systems. This technique is essential for simplifying complicated integrals and solving real-world problems in physics and engineering. The connection to U-substitution from Calculus 2 helps students bridge their previous knowledge with new concepts, making the learning process more intuitive. As students progress through Calculus 3, they'll find that change in variables becomes an indispensable tool in their mathematical toolkit, enabling them to approach complex problems with confidence and efficiency.

    FAQs

    1. What is the change in variables technique in calculus?

      The change in variables technique, also known as substitution, is a method used in calculus to simplify complex integrals by transforming them into more manageable forms. It involves replacing the original variables with new ones, often changing the coordinate system or the shape of the integration region. This technique is particularly useful for solving multivariable problems and simplifying complicated integrals.

    2. How does the Jacobian relate to change in variables?

      The Jacobian is a crucial component in the change of variables process. It's a matrix of partial derivatives that represents how a transformation affects areas or volumes in different coordinate systems. When changing variables in an integral, the absolute value of the Jacobian determinant is multiplied by the integrand to account for the stretching or compression of space caused by the transformation.

    3. What are some common coordinate transformations used in calculus?

      Common coordinate transformations include:

      • Cartesian to polar coordinates (and vice versa)
      • Cartesian to spherical coordinates
      • Cartesian to cylindrical coordinates
      • Various geometric transformations like translation, rotation, and scaling

      These transformations are chosen based on the problem's geometry and can significantly simplify complex integrals.

    4. How does changing variables help in solving real-world problems?

      Changing variables is invaluable in solving real-world problems across various fields. In physics, it can simplify equations of motion in rotational systems. In engineering, it aids in analyzing fluid dynamics and complex electrical circuits. In statistics, it's used to derive new probability distributions. This technique allows professionals to model and solve complex phenomena more efficiently, leading to advancements in their respective fields.

    5. What are the key steps in applying the change of variables technique to a double integral?

      The key steps are:

      1. Choose appropriate new variables
      2. Express old variables in terms of new ones
      3. Find the new region of integration
      4. Transform the integrand function
      5. Calculate the Jacobian
      6. Set up the new integral with the Jacobian
      7. Evaluate the transformed integral

      This process allows for the transformation of complex integrals into more solvable forms, often simplifying the calculation significantly.

    Prerequisites

    Understanding the concept of "Change in variables" is crucial in mathematics, particularly in calculus and geometry. To fully grasp this topic, it's essential to have a solid foundation in certain prerequisite areas. Two key prerequisites that play a significant role in comprehending change in variables are polar coordinates and rotational symmetry and transformations.

    Let's start by exploring the importance of polar coordinates in relation to change in variables. Polar coordinates provide an alternative way to represent points in a two-dimensional plane, using distance from the origin and an angle, rather than x and y coordinates. This system is particularly useful when dealing with circular or spiral patterns, which are common in many real-world applications. When studying change in variables, understanding polar coordinates is crucial because it allows us to transform between different coordinate systems. This polar coordinates transformation is a perfect example of how variables can change while still describing the same point or function.

    The concept of rotational symmetry and transformations is another vital prerequisite for grasping change in variables. Rotational symmetry occurs when an object looks the same after being rotated by a certain angle. This concept is closely tied to the idea of transformations, which involve moving or changing the shape of geometric figures. When we talk about change in variables, we're often dealing with transformations of functions or equations. Understanding rotational symmetry helps us visualize how these changes affect the overall structure and behavior of mathematical objects.

    The interplay between these prerequisites and change in variables becomes evident in various mathematical scenarios. For instance, when converting a function from Cartesian to polar coordinates, we're essentially performing a change of variables. This process requires a solid understanding of both coordinate systems and how to transform between them. Similarly, when applying rotational transformations to functions or equations, we're changing the variables in a way that preserves certain symmetrical properties.

    Moreover, these prerequisite topics provide the necessary tools for analyzing and solving problems involving change in variables. Polar coordinates offer a more intuitive approach to dealing with circular motion and radial functions, while rotational symmetry and transformations help in simplifying complex problems by exploiting their inherent symmetrical properties.

    In conclusion, mastering the concepts of polar coordinates and rotational symmetry and transformations is essential for a comprehensive understanding of change in variables. These prerequisites not only provide the foundational knowledge required but also offer different perspectives and problem-solving techniques that are invaluable in higher-level mathematics. By thoroughly grasping these concepts, students will be better equipped to tackle more advanced topics and applications involving change in variables across various fields of mathematics and science.