Sign In
Sign Up
flag-uk

Mastering 3D Coordinate Systems: Navigate the Third Dimension
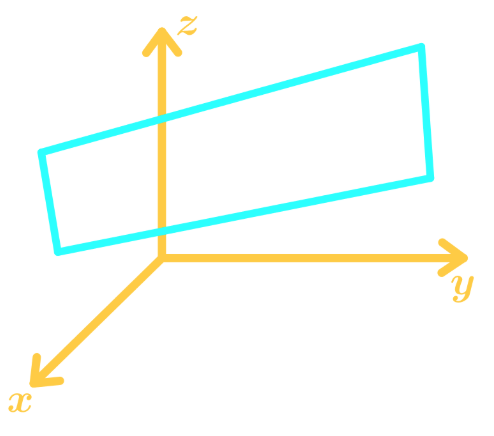
Unlock the power of 3D coordinate systems! Learn to visualize points, planes, and shapes in three dimensions. Discover real-world applications in physics, engineering, and computer graphics.

  1. Intros0/3 watched
  2. Examples0/7 watched
  1. 0/3
  2. 0/7
Now Playing:3 d coordinate system – Example 0a
Intros
0/3 watched
  1. 3-D Coordinate System Overview:
  2. 3-D Coordinate System Overview:
    R,R2,and  R3 \mathbb{R}, \mathbb{R}^2, \mathrm{and} \;\mathbb{R}^3
    • Axis in 1D, 2D, and 3D
    • Points in 3D
    • xyxy-plane, xzxz-plane, and yzyz-plane
  3. 3-D Coordinate System Overview:
    Projection & Distance of points
    • Projection of a point on a plane
    • Distance between two points in 3D
    • Knowing and Applying the formula
Examples
0/7 watched
  1. Finding Projection of Points
    Find the projection of the point (−3,1,5)(-3, 1 ,5) onto the yzyz-plane.
    3-D coordinate system
    Jump to:NotesConceptFAQsPrerequisites
    Notes
    Notes:

    3-D Coordinate System
    In the 3-D Coordinate System, also denoted as R3\mathbb{R}^3, we have 3 axis (x,y,z) (x,y,z) . We draw the axis' in the graph like this:
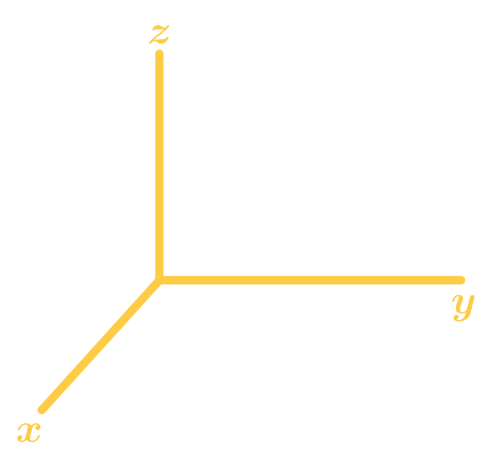
    3d coor system
    Points are written in the form P=(x,y,z)P=(x,y,z)


    Planes
    The xyxy-plane corresponds to all the points at which z=0z=0.
    The xzxz-plane corresponds to all the points at which y=0y=0.
    The yzyz-plane corresponds to all the points at which x=0x=0.

    These planes are sometimes called "coordinate planes".


    Projection of a Point
    When a point P=(x1,y1,z1)P=(x_1,y_1,z_1) gets projected onto a plane, then the point will be on the plane.
    For example, the projection of point P=(x1,y1,z1) P=(x_1,y_1,z_1) onto the xyxy-plane will become (x1,y1,0)(x_1,y_1,0).


    Distance of Two Points To find the distance between two points in R3\mathbb{R}^3, we use the formula:

    D=(x2−x1)2+(y2−y1)2+(z2−z1)2D = \sqrt{(x_2-x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}

    Where the two points are P=(x1,y1,z1)P=(x_1,y_1,z_1) and Q=(x2,y2,z2)Q=(x_2,y_2,z_2).


    Other General Equations in 3D
    Here are the general types of equations you might see in the 3-D Coordinate system:

    1. Cylinder: (x−a)2+(y−b)2=r2(x-a)^2 + (y-b)^2 = r^2
      cylinder
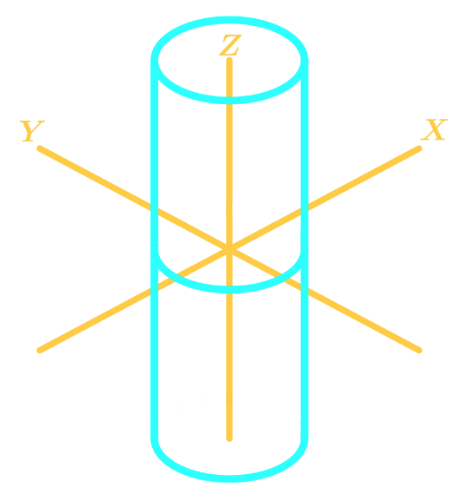
      Points are written in the form P=(x,y,z)P=(x,y,z)
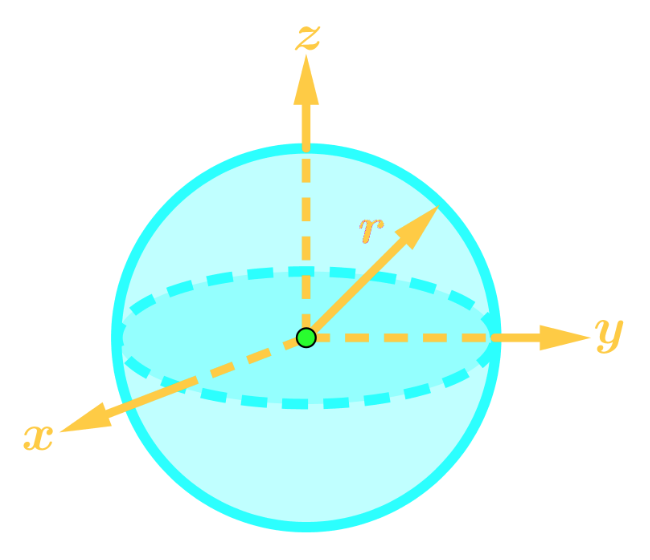
    2. Sphere: (x−a)2+(y−b)2+(z−c)2=r2 (x-a)^2+(y-b)^2+(z-c)^2=r^2
      sphere
      Points are written in the form P=(x,y,z)P=(x,y,z)
    3. Plane: ax+by+cz=dax+by+cz=d
      plane
    Concept

    Introduction to 3D Coordinate Systems

    Welcome to the fascinating world of Calculus 3! As we embark on this journey, we'll be exploring the 3D coordinate system, a crucial concept that forms the foundation of our studies. Unlike the 2D plane you're familiar with from earlier math courses, the 3D coordinate system adds depth to our mathematical understanding. This system allows us to represent and analyze objects in three-dimensional space, opening up a whole new realm of possibilities. To help you transition smoothly from 2D to 3D thinking, we've prepared an introduction video that visually demonstrates these concepts. This video is designed to make the leap into 3D space feel natural and intuitive. By mastering the 3D coordinate system, you'll be well-equipped to tackle more advanced topics in Calculus 3, such as vector calculus, surface integrals, and multivariable functions. So, let's dive in and explore this exciting new dimension of mathematics together!

    FAQs

    Here are some frequently asked questions about 3D coordinate systems:

    1. What is a 3D coordinate system?

      A 3D coordinate system is a mathematical framework used to describe the position of points, lines, and shapes in three-dimensional space. It typically consists of three perpendicular axes: x, y, and z. Each point in 3D space is represented by an ordered triple (x, y, z), indicating its position relative to these axes.

    2. How does a 3D coordinate system differ from a 2D system?

      While a 2D coordinate system uses two axes (x and y) to represent points on a plane, a 3D system adds a third axis (z) to represent depth. This allows for the representation of objects and spaces with volume, enabling more complex geometric analysis and visualization.

    3. What are some real-world applications of 3D coordinate systems?

      3D coordinate systems are used in various fields, including computer graphics for video games and movies, 3D modeling and printing, robotics, navigation systems (GPS), architectural design, and scientific simulations. They're essential in physics for describing motion and forces, and in engineering for designing complex structures and machines.

    4. How do you calculate distance between two points in 3D space?

      The distance between two points (x, y, z) and (x, y, z) in 3D space is calculated using the formula: d = ((x - x)² + (y - y)² + (z - z)²). This is an extension of the Pythagorean theorem to three dimensions.

    5. What are projections in 3D coordinate systems?

      Projections in 3D coordinate systems involve mapping 3D points onto a 2D plane. This is crucial in creating 2D representations of 3D objects, such as in technical drawings or computer displays. Common projections include orthographic (showing objects as viewed from directly above, in front, or from the side) and perspective projections (simulating how objects appear to the human eye, with distant objects appearing smaller).

    Prerequisites

    Mastering the 3-D coordinate system is crucial for various fields, including mathematics, physics, and computer graphics. However, to fully grasp this concept, it's essential to have a solid foundation in several prerequisite topics. Understanding these fundamental concepts will significantly enhance your ability to work with three-dimensional space and solve complex problems.

    One of the most critical prerequisites is the Euclidean distance formula. This formula is the cornerstone for measuring distances between points in space. In a 3-D coordinate system, you'll frequently need to calculate distances between objects or points, and the distance formula provides the mathematical tool to do so accurately. By mastering this concept in two dimensions, you'll be well-prepared to extend it to three-dimensional space.

    Another crucial skill is graphing 2D equations. Understanding how to determine the number of solutions to linear equations and visualize them on a 2-D plane is a stepping stone to working in 3-D. This knowledge helps you comprehend how equations represent surfaces in three-dimensional space and how different equations intersect to form lines or points. The ability to mentally visualize these concepts is invaluable when dealing with complex 3-D problems.

    Lastly, familiarity with vector operations in 3D space is essential. Vectors are fundamental to describing motion, forces, and positions in three dimensions. Understanding vector components allows you to break down complex 3-D movements into manageable parts along each axis. This skill is particularly useful in physics and engineering applications of the 3-D coordinate system.

    By building a strong foundation in these prerequisite topics, you'll be well-equipped to tackle the challenges of the 3-D coordinate system. The distance formula will help you measure spatial relationships, graphing skills will aid in visualizing complex equations, and vector operations will enable you to describe and analyze movement in three-dimensional space. Together, these concepts form the building blocks for advanced study and application of 3-D coordinates in various scientific and technical fields.

    Remember, mathematics and physics are cumulative subjects. Each new concept builds upon previous knowledge. Taking the time to thoroughly understand these prerequisites will not only make learning about the 3-D coordinate system easier but will also provide you with a robust toolkit for solving a wide range of spatial problems. As you progress, you'll find that these fundamental concepts continually resurface, reinforcing their importance in your mathematical journey.