Bearings and direction word problems

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

Get the most by viewing this topic in your current grade. Pick your course now.

?
Intros
Lessons
  1. Introduction to Bearings and Direction Word Problems
?
Examples
Lessons
  1. Evaluate A Bearings Word Problem Using Trigonometric Ratios

    Charlie leaves home for a bike ride, heading 040°T for 5km.

    1. How far north or south is Charlie from its starting point?
    2. How far east or west is Charlie from its starting point?
  2. Solve A Bearings Word Problem Using the Law of Cosine

    A camping group made a return journey from their base camp. From the camp, they first travelled 120°T for 3km. Then they travelled 210°T for 9km. Determine the direction and distance they need to travel if they want to return to the base camp now.

    1. Analyze A Bearings Word Problem Using Trigonometric Ratios and the Law of Cosine

      Melody and April go to the same school. Melody's home is 3.5km with a bearing of S16°W from school whilst April's home is 2.4km with a bearing of N42°E from school. How far away are their homes from each other?

      1. Triangulate the Location of an Earthquake

        Radar X detected an earthquake N55°E of it. 16km due east of Radar X, Radar Y detected the same earthquake N14°W of it.

        1. Determine the earthquake from Radar X and Y.
        2. Which Radar is closer to the earthquake?
      2. Estimate the Height of an Object

        A plane is sighted by Tom and Mary at bearings 028°T and 012°T respectively. If they are 2km away from each other, how high is the plane?

        1. Applying Law of Sine and Law of Cosine

          Consider the following diagram.

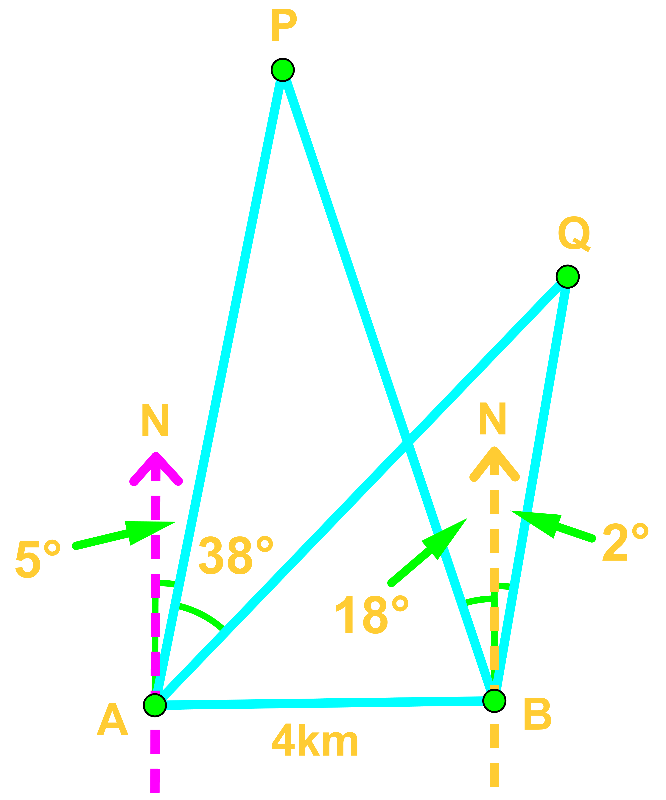
          Applying Law of Sine and Law of Cosine

          Find the distance between P and Q.

          Topic Notes
          ?

          Theorems that are useful:

          Pythagorean Theorem: a2+b2=c2a^{2} + b^{2} = c^{2}

          Trig ratio: sin⁡θ=OH\sin \theta = \frac{O}{H}

          cos⁡θ=AH\cos \theta = \frac{A}{H}

          tan⁡θ=OA\tan \theta = \frac{O}{A}

          Law of sine: asin⁡A=bsin⁡B=csin⁡C\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}

          Law of cosine: c2=a2+b2−2abcos⁡Cc^{2} = a^{2} + b^{2} - 2ab \cos C