Path Counting: Unlocking the Power of Combinatorial Problem Solving Dive into the world of path counting and master essential problem-solving techniques. From basic grids to complex scenarios, learn how to tackle challenges with confidence and precision.
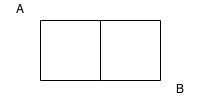
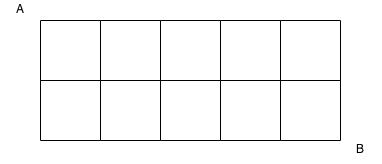
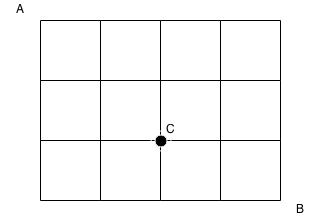
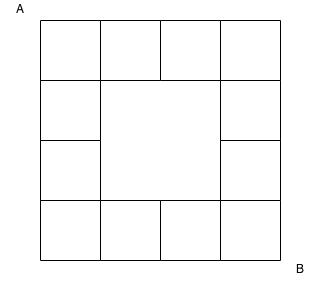
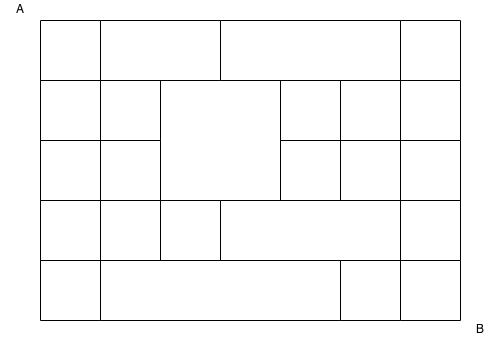
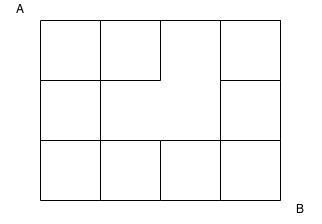
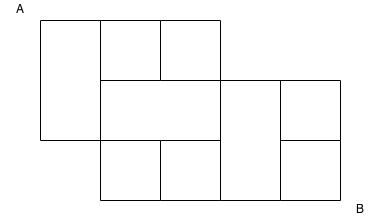
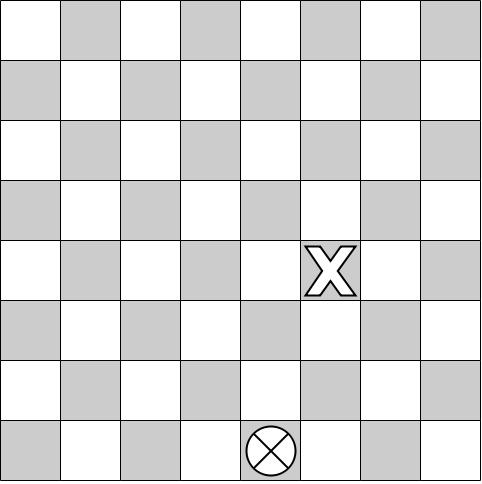
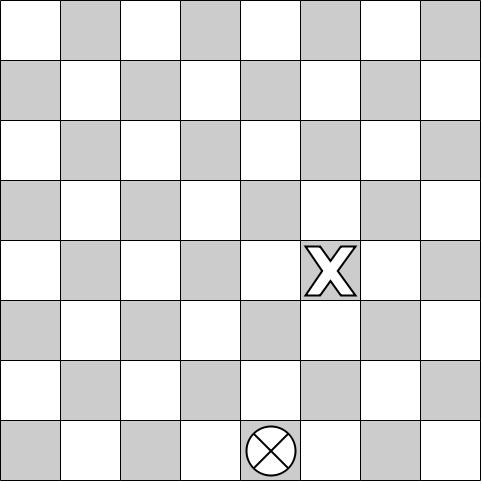
- Moving only the right or down, how many different paths exist to get from point A to point B?
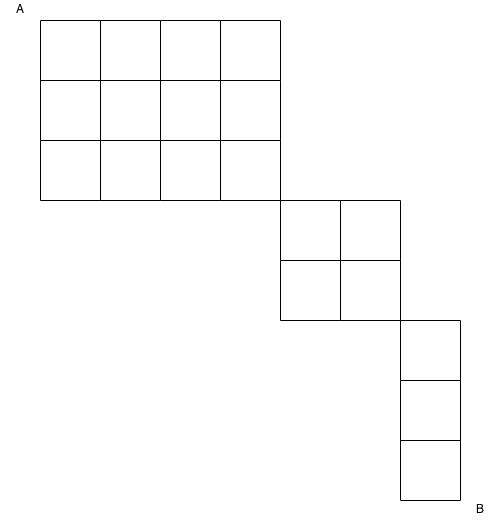
- Irregular Puzzle
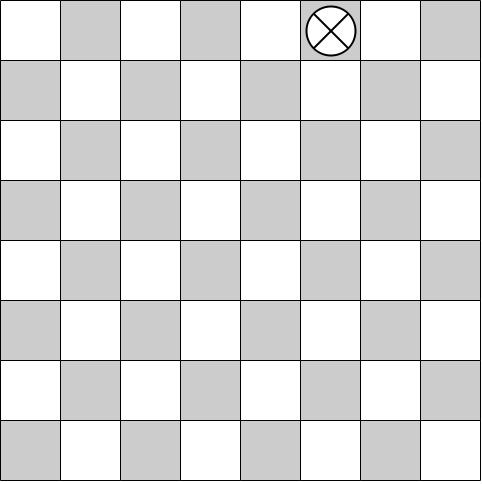
- Below is an 8 × 8 checkerboard. The game pieces are only allowed to move diagonally and forward on the dark squares. How many possible ways are there for the checker to reach the opposite side of the game board, if:
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction to Path Counting Problems
Welcome to the fascinating world of path counting problems in mathematics! These intriguing puzzles are not just fun to solve, but they also play a crucial role in various fields like computer science, network analysis, and probability theory. Path counting problems challenge us to determine the number of possible routes from one point to another, often with specific constraints or rules. Our introduction video provides a visual and engaging explanation of this concept, making it easier for you to grasp the fundamentals. As your math tutor, I'm excited to guide you through this journey of discovery. By understanding path counting, you'll develop critical thinking skills and gain insights into combinatorics, a branch of mathematics that deals with counting and arrangements. Whether you're a beginner or looking to refresh your knowledge, this video will serve as an excellent starting point for your exploration of path counting problems. Let's dive in and unravel the mysteries of these mathematical challenges together!
-
What is the difference between the visualization and counting methods for path counting problems?
The visualization method involves drawing out all possible paths, which is intuitive but time-consuming for larger grids. The counting method uses systematic addition along diagonals, making it more efficient for complex problems. Visualization is best for small grids and beginners, while counting is preferred for larger grids and more advanced problems.
-
How does the factorial method simplify path counting in large grids?
The factorial method uses the formula: Number of paths = n! / (r! × d!), where n is the total steps, r is right steps, and d is down steps. This approach is highly efficient for large grids as it doesn't require drawing paths or step-by-step counting. It's especially useful when the grid size increases, making manual counting impractical.
-
Can path counting methods be applied to real-world scenarios?
Yes, path counting has numerous real-world applications. It's used in computer science for algorithm optimization, in biology for studying genetic sequences, and in urban planning for traffic flow analysis. These methods also apply to network analysis, probability theory, and even in social sciences for analyzing decision-making processes.
-
How do you handle obstacles or restricted movements in path counting problems?
For problems with obstacles or restricted movements, the counting method is often most effective. Assign a value of 0 to cells representing obstacles and proceed with diagonal addition. This approach allows for handling complex path restrictions without significantly increasing calculation complexity. For very irregular puzzles, breaking the grid into sections and counting paths for each section separately may be necessary.
-
What skills does practicing path counting problems develop?
Practicing path counting problems develops critical thinking, problem-solving skills, and mathematical reasoning. It enhances understanding of combinatorics and probability theory. These exercises also improve spatial reasoning, pattern recognition, and the ability to approach complex problems systematically. Additionally, mastering these techniques provides a foundation for more advanced topics in mathematics and computer science.
Understanding path counting problems requires a solid foundation in several key mathematical concepts. Two crucial prerequisite topics that significantly contribute to mastering path counting are probability involving permutations and combinations and solving systems of linear equations by elimination.
The concept of permutations and combinations is fundamental to path counting problems. When dealing with these problems, we often need to calculate the number of possible ways to arrange objects or select items from a set. This is where permutations and combinations come into play. Understanding how to calculate these arrangements and selections is crucial for determining the total number of possible paths in various scenarios.
For instance, in a grid-based path counting problem, knowing how to apply combinatorial principles helps in calculating the number of unique paths from one point to another. The ability to recognize and apply these concepts efficiently can significantly simplify complex path counting problems.
On the other hand, solving systems of linear equations by elimination, particularly using the diagonal addition method, might seem less directly related but is equally important. This skill becomes invaluable when dealing with more advanced path counting problems that involve multiple constraints or conditions.
In some path counting scenarios, you may encounter situations where you need to solve simultaneous equations to determine the number of paths satisfying certain criteria. The ability to efficiently solve these equations using elimination techniques can be a game-changer in tackling complex problems.
Moreover, the logical thinking and problem-solving skills developed while learning to solve systems of equations transfer well to path counting problems. Both require a systematic approach, careful analysis of given information, and the ability to break down complex problems into manageable steps.
By mastering these prerequisite topics, students build a strong foundation for understanding and solving path counting problems. The skills acquired in working with permutations and combinations provide the necessary tools for enumerating possibilities, while proficiency in solving linear equations enhances analytical and problem-solving abilities.
In conclusion, a solid grasp of these prerequisite topics not only facilitates a smoother learning experience when tackling path counting problems but also equips students with versatile mathematical skills applicable to a wide range of advanced topics in mathematics and related fields.