Scalar Quantity: a quantity having only magnitude but not direction
Two – Dimensional Vectors:
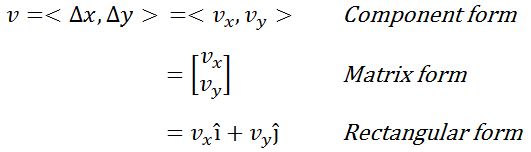
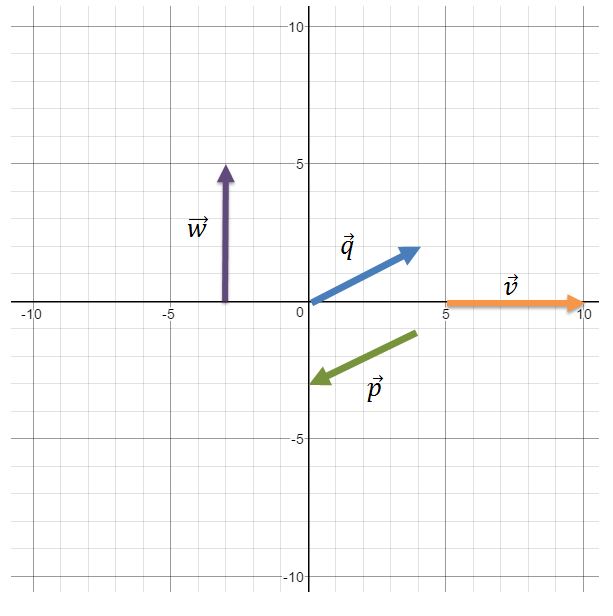
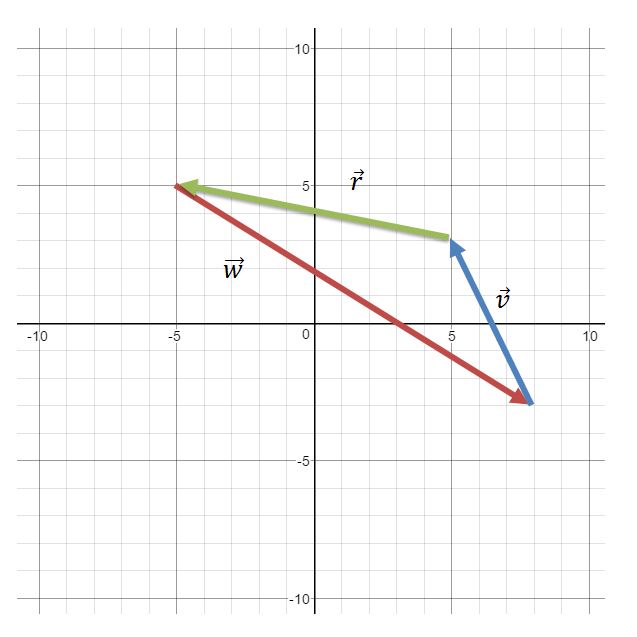



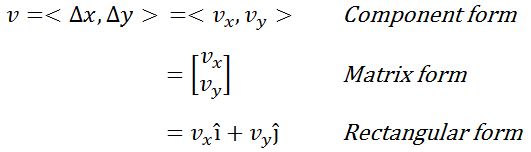
Vectors are fundamental mathematical concepts that play a crucial role in our daily lives, often without us realizing it. The introduction video provides an essential foundation for understanding these powerful tools. Vectors are quantities that possess both magnitude and direction, making them invaluable in various fields. In everyday scenarios, vectors are at work in airplane navigation, guiding pilots through complex flight paths. Video game developers use vectors to create realistic character movements, enhancing gameplay experiences. From physics to engineering, vectors help describe and analyze motion, forces, and spatial relationships. They enable us to represent and manipulate multidimensional data efficiently. As we delve deeper into the world of vectors, we'll discover their applications in GPS technology, weather forecasting, and even in the optimization of delivery routes. Understanding vectors opens up a new perspective on the world around us, revealing the underlying mathematical structure of many natural and technological phenomena.
A vector is a quantity that has both magnitude and direction, while a scalar only has magnitude. For example, velocity is a vector because it includes speed (magnitude) and direction, whereas temperature is a scalar because it only has a numerical value without direction.
Vectors are typically represented graphically as arrows. The length of the arrow indicates the magnitude of the vector, while the direction the arrow points shows the vector's direction. This visual representation makes it easier to understand and work with vectors in various applications.
Vectors have numerous real-world applications, including:
To add two vectors, you add their corresponding components. For example, if you have vector A (3, 2) and vector B (1, 4), the sum would be (3+1, 2+4) = (4, 6). Graphically, this can be represented by placing the tail of one vector at the head of the other and drawing a new vector from the tail of the first to the head of the second.
Understanding vectors is crucial in STEM fields because they provide a powerful tool for describing and analyzing phenomena that involve both magnitude and direction. Vectors are essential in physics for representing forces and motion, in engineering for structural analysis and design, and in computer science for graphics and simulations. Mastering vector concepts enhances problem-solving skills and opens up opportunities in various scientific and technological careers.
Understanding the fundamentals of vectors is crucial for success in various fields of mathematics and physics. Before diving into an introduction to vectors, it's essential to grasp several key prerequisite topics that form the foundation for vector concepts.
One of the most important prerequisites is understanding operations on vectors in magnitude and direction form. This knowledge allows students to manipulate vectors effectively, which is a core skill in vector mathematics. Familiarity with magnitude and direction helps in visualizing and calculating vector properties in various contexts.
Another critical prerequisite is the ability to perform vector addition and subtraction. These operations are fundamental to vector algebra and are often applied in physics problems involving forces or velocities. Understanding how to solve linear equations using addition and subtraction provides a solid basis for these vector operations.
Knowledge of vector components is also essential. This concept helps in breaking down complex vectors into simpler, manageable parts, making it easier to perform calculations and analyze vector behavior in different dimensions. Mastering vector components is crucial for advanced vector operations and applications in physics and engineering.
Lastly, comprehending the magnitude of a vector is fundamental to vector analysis. The magnitude represents the "size" or "length" of a vector, which is a key characteristic in many vector-related problems. Understanding how to calculate and interpret vector magnitudes is vital for solving a wide range of vector problems in mathematics and physics.
These prerequisite topics collectively provide a strong foundation for studying vectors. They enable students to grasp the concept of vectors as quantities with both magnitude and direction, understand how vectors interact and combine, and apply vector principles to solve real-world problems. By mastering these prerequisites, students will be well-prepared to tackle more advanced vector concepts and applications in their studies and future careers in fields such as physics, engineering, and computer graphics.
As students progress in their understanding of vectors, they'll find that these prerequisite topics are not just isolated concepts but interconnected ideas that continually resurface and build upon each other. This interconnectedness highlights the importance of thoroughly understanding each prerequisite before moving on to more complex vector topics. With a solid grasp of these fundamentals, students will be well-equipped to explore the fascinating world of vectors and their wide-ranging applications in science and technology.
