Sign In
Sign Up
flag-sg

Mastering Dot Product in Vector Mathematics
Dive into the world of dot product, a fundamental concept in vector algebra. Learn its properties, applications in physics, and how it relates to vector projections and magnitudes.

  1. Intros0/3 watched
  2. Examples0/6 watched
  1. 0/3
  2. 0/6
Now Playing:Dot product – Example 0a
Intros
0/3 watched
  1. Dot Product Overview:
  2. Dot Product Overview:
    Dot Product and its Special Property
    • Multiplying the corresponding entries, and adding
    • Dot product = 0 →\to vectors are perpendicular
  3. Dot Product Overview:
    Application to Dot Product
    • What is scalar projection? Vector projection
    • Formula for scalar projection: ∣v∣=a⋅b∣b∣|v| = \frac{a \cdot b}{|b|}
    • Formula for vector projection v=a⋅bb⋅bbv = \frac{a \cdot b}{b \cdot b}b
Examples
0/6 watched
  1. Using the Dot Product
    Find the dot product of u=<−1,−2,7> u = <-1, -2 , 7> and v=<−2,1,−2>v = <-2,1,-2> .
    3-D coordinate system
    Jump to:NotesConceptFAQsPrerequisites
    Notes
    Notes:

    Dot Product
    Let u=<a,b,c>u=<a,b,c> and v=<d,e,f>v=<d,e,f>. Then the dot product of these two vectors will be:

    u⋅v=ad+be+dfu \cdot v = ad + be + df

    Dot Product Property
    If the dot product of two vectors uu and vv gives 0, then the vectors are perpendicular. In other words,

    u⋅v=0→u \cdot v=0 \to perpendicular vectors

    Scalar and Vector Projection
    Suppose we have two vectors aa and bb. Suppose they create an angle θ\theta such that we get the following picture:
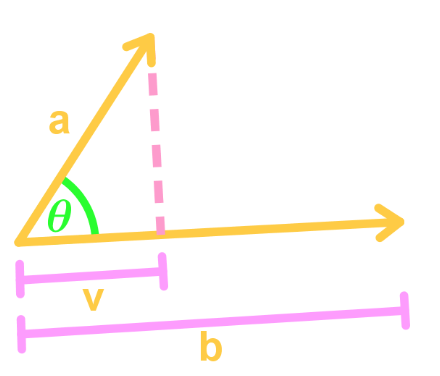
    projection

    ∣v∣=a⋅b∣b∣ |v| = \frac{a \cdot b } {|b|}

    To find the vector projection aa onto bb (which is v), we use the formula:

    v=a⋅bb⋅bb v = \frac{a \cdot b}{b \cdot b}b

    Additional Dot Product Properties
    Let u,v,wu, v, w be vectors and cc be a scalar. Then the properties of dot products are:
    1. u⋅u=∣u∣2u \cdot u = |u|^2
    2. u⋅v=v⋅uu \cdot v = v \cdot u
    3. u⋅(v+w)=u⋅v+u⋅wu \cdot (v+w) = u \cdot v + u \cdot w
    4. (cu)⋅v=u⋅(cv)=c(u⋅v) (cu) \cdot v = u \cdot (cv) = c(u \cdot v)
    Concept

    Introduction to Dot Product

    Welcome to our exploration of the dot product, a fundamental concept in vector mathematics! The dot product, also known as the scalar product, is a powerful tool that allows us to calculate the relationship between two vectors. It's essential in various fields, from physics to computer graphics. Before we dive deeper, I highly recommend watching our introduction video. This video provides a visual and intuitive understanding of the dot product, making it easier to grasp the concept. As your math tutor, I'm excited to guide you through this topic. The dot product helps us determine the angle between vectors, calculate vector projections, and even measure how similar two vectors are. It's a versatile concept that you'll find incredibly useful as you progress in your mathematical journey. So, let's start with the basics and build our understanding step by step. Are you ready to unlock the power of the dot product?

    FAQs

    Here are some frequently asked questions about dot product:

    1. What is the dot product of two vectors?

      The dot product of two vectors is a scalar value obtained by multiplying the corresponding components of the vectors and then summing the results. For vectors A = (a1, a2, a3) and B = (b1, b2, b3), the dot product is calculated as A · B = a1b1 + a2b2 + a3b3.

    2. How is the dot product related to vector magnitude?

      The dot product of a vector with itself is equal to the square of its magnitude. For a vector A, A · A = |A|². This property is useful for calculating vector magnitudes without using the square root function directly.

    3. What does a zero dot product indicate?

      A zero dot product between two non-zero vectors indicates that the vectors are perpendicular (orthogonal) to each other. This property is often used to check if vectors are at right angles in various applications, such as computer graphics and physics simulations.

    4. How is the dot product used in physics?

      In physics, the dot product is used in many applications, including calculating work done by a force (W = F · d), determining power in electrical circuits (P = V · I), and analyzing projections of vectors. It's also crucial in understanding concepts like torque and angular momentum.

    5. Can you explain the geometric interpretation of the dot product?

      Geometrically, the dot product of two vectors A and B can be interpreted as A · B = |A| |B| cos(θ), where θ is the angle between the vectors. This interpretation is useful for finding angles between vectors and understanding the concept of vector projections in various applications.

    Prerequisites

    Mastering the concept of dot product in mathematics and physics requires a solid foundation in several key areas. One of the most fundamental prerequisites is understanding vector components. This concept is crucial because dot product involves the multiplication and summation of vector components. By grasping how vectors are broken down into their constituent parts, students can more easily comprehend the mechanics of dot product calculations.

    Another essential prerequisite is the ability to apply the distributive property in linear equations. This algebraic skill is directly applicable to dot product operations, as the distributive property of dot product is a key principle in vector algebra. Understanding how to distribute terms in equations prepares students for the similar process in dot product calculations.

    Familiarity with the magnitude of a vector is also crucial when studying dot product. The dot product is intimately related to vector magnitudes, as it can be expressed in terms of the magnitudes of the vectors involved and the angle between them. This relationship is fundamental in many applications of dot product, particularly in physics and engineering.

    Lastly, a strong foundation in trigonometry, especially in SohCahToa and related concepts, is invaluable when working with dot products. These trigonometric principles are essential for understanding and deriving the angle formula for dot product, which relates the dot product to the angle between two vectors. This connection between trigonometry and vector operations is a cornerstone of many advanced mathematical and physical concepts.

    By mastering these prerequisite topics, students build a robust framework for understanding dot product. Vector components provide the basic language of vector operations, while the distributive property offers a familiar algebraic tool that extends naturally to vector mathematics. Understanding vector magnitudes gives context to the scalar nature of dot product results, and trigonometric knowledge bridges the gap between geometric intuition and algebraic manipulation in vector spaces.

    Moreover, these prerequisites are not isolated concepts but interconnected ideas that form a cohesive foundation for advanced mathematics and physics. For instance, the ability to work with vector components enhances understanding of vector magnitudes, which in turn relates to trigonometric concepts when considering angles between vectors. Similarly, the distributive property in algebra finds new applications in vector operations, illustrating the beautiful continuity of mathematical ideas across different domains.

    In conclusion, a thorough grasp of these prerequisite topics not only facilitates learning about dot product but also enriches overall mathematical understanding. It equips students with a versatile toolkit applicable to a wide range of problems in physics, engineering, and advanced mathematics, making the study of dot product a gateway to more complex and fascinating areas of quantitative sciences.