Dividing decimals with integers

Introduction to Dividing Decimals by Integers

Welcome to our lesson on dividing decimals by integers! This fundamental math skill is crucial for many real-world applications. To kick things off, we've prepared an introduction video that will give you a solid foundation for understanding this concept. The video breaks down the process step-by-step, making it easier to grasp. Dividing decimals by integers might seem tricky at first, but with practice, you'll find it's quite manageable. Remember, when dividing a decimal by an integer, the decimal point in the quotient stays directly above the decimal point in the dividend. This key rule will help you keep your calculations organized. As we progress, we'll explore various strategies and shortcuts to make these calculations even simpler. Don't worry if it doesn't click immediately we'll work through plenty of examples together to reinforce your understanding. Let's dive in and master this essential math skill!

Understanding Integers and Decimals

When we think about numbers, it's helpful to visualize them on a number line. This simple tool can help us understand the relationship between different types of numbers, particularly integers and decimals, as well as positive and negative numbers.

Integers are whole numbers that can be positive, negative, or zero. On a number line, integers are represented by evenly spaced points. For example, ...-3, -2, -1, 0, 1, 2, 3... are all integers. They're the numbers we use for counting and basic arithmetic.

Decimals, on the other hand, are numbers that have a fractional part. On the number line, decimals fill in the spaces between integers. For instance, 1.5 would be halfway between 1 and 2 on the number line. Decimals allow us to represent more precise values and are essential in many real-world applications, from measuring ingredients in cooking to calculating distances in science.

Now, let's talk about positive and negative numbers. Imagine the number line stretching infinitely in both directions from zero. Numbers to the right of zero are positive, while those to the left are negative. Zero itself is neither positive nor negative; it's the point where the two sides meet.

Positive numbers represent quantities greater than zero. On the number line, they extend to the right of zero and increase in value as they move further away. For example, 1, 2.5, and 10 are all positive numbers.

Negative numbers, conversely, represent quantities less than zero. They extend to the left of zero on the number line and become more negative (or smaller) as they move further away. For instance, -1, -2.5, and -10 are negative numbers.

The relationship between positive and negative numbers is fascinating. Each positive number has a negative counterpart, called its opposite, located the same distance from zero but on the other side of the number line. For example, 3 and -3 are opposites, as are 1.5 and -1.5.

Understanding this relationship is crucial in many mathematical operations. When we add a positive and negative number, we're essentially finding the difference between their absolute values. For instance, 5 + (-3) is the same as 5 - 3, which equals 2.

The number line also helps us visualize the concept of absolute value. The absolute value of a number is its distance from zero on the number line, regardless of whether it's positive or negative. For example, both 4 and -4 have an absolute value of 4, as they're both four units away from zero.

In real-world applications, positive and negative numbers are used to represent various quantities. Positive numbers might represent gains, increases, or temperatures above freezing, while negative numbers could indicate losses, decreases, or temperatures below freezing.

As we delve deeper into mathematics, understanding integers, decimals, and their positive and negative counterparts becomes increasingly important. These concepts form the foundation for more advanced mathematical ideas and are essential in fields ranging from finance to physics.

Remember, the number line is a powerful tool for visualizing these relationships. Whether you're working with whole numbers or fractions, positive or negative values, the number line can help you see how these numbers relate to each other and to zero. By mastering these fundamental concepts, you'll be well-equipped to tackle more complex mathematical challenges in the future.

Rules for Dividing Decimals by Integers

Let's dive into the exciting world of dividing decimals by integers! Imagine you're planning a party, and you want to make sure everyone has a great time. In this party analogy, we'll use happy faces to represent positive numbers and sad faces for negative numbers.

First, let's review the basic division rules:

1. When dividing a decimal by an integer, the decimal point in the answer stays in the same position as in the decimal number you're dividing.
2. Divide as you would with whole numbers, but remember to bring the decimal point straight up into your answer.
3. If needed, add zeros after the last decimal place to continue dividing until you get a remainder of zero or a repeating decimal.

Now, let's talk about determining if the result will be positive or negative. This is where our party guests come in!

Imagine you're inviting people to your party. The division rules for positive and negative numbers work just like the multiplication rules:

• ÷ = (Positive ÷ Positive = Positive)
• ÷ = (Negative ÷ Negative = Positive)
• ÷ = (Positive ÷ Negative = Negative)
• ÷ = (Negative ÷ Positive = Negative)

Think of it this way: When you're dividing two numbers with the same sign (both positive or both negative), it's like inviting friends who all get along. The result is a happy party (positive answer)! But when you divide numbers with different signs, it's like inviting people who don't get along, resulting in a not-so-happy party (negative answer).

Let's look at some examples:

1. 12.6 ÷ 3 = 4.2 (Positive ÷ Positive = Positive)
2. -8.4 ÷ 2 = -4.2 (Negative ÷ Positive = Negative)
3. 15.9 ÷ (-3) = -5.3 (Positive ÷ Negative = Negative)
4. -24.6 ÷ (-6) = 4.1 (Negative ÷ Negative = Positive)

Remember, when dividing decimals by integers, follow these steps:

1. Identify the signs of both numbers to determine if the result will be positive or negative.
2. Set up the division problem, keeping the decimal point in the same position in the dividend (the number being divided).
3. Divide as you would with whole numbers, bringing the decimal point straight up into your answer.
4. Continue dividing, adding zeros after the last decimal place if needed, until you get a remainder of zero or a repeating decimal.

Practice makes perfect! Try solving these practice decimal division problems:

• 18.6 ÷ 3 = ?
• -7.2 ÷ 4 = ?
• 5.4 ÷ (-2) = ?
• -10.8 ÷ (-9) = ?

Remember, just like planning a party, dividing decimals by integers can be fun and rewarding when you follow the rules and keep track of your happy and sad faces (positive and negative numbers). With practice, you'll become a division party planner extraordinaire!

Using Mental Math for Simple Decimal Division

Mental math is a valuable skill that can make everyday calculations much easier, especially when it comes to dividing decimals by integers. In this section, we'll explore a simple two-step process that will help you perform these divisions quickly and accurately in your head. Let's dive into the world of decimal division using mental math techniques!

The first step in our mental math method for dividing decimals by integers is determining the sign of the answer. This is a crucial step that sets the foundation for the rest of the calculation. When dividing two numbers with the same sign (both positive or both negative), the result will be positive. Conversely, when dividing numbers with different signs (one positive and one negative), the result will be negative. Keep this rule in mind as we move forward with our calculations.

Once we've determined the sign, we move on to the second step: dividing each place value. This is where the real mental math magic happens! We'll start with the leftmost digit and work our way to the right, dividing each digit by our integer. If there's a remainder, we'll carry it over to the next place value. This step-by-step approach allows us to break down the problem into manageable chunks, making it easier to solve in our heads.

Let's illustrate this process with a detailed example: 6.482 ÷ (-2). First, we determine the sign. Since we're dividing a positive number by a negative number, our result will be negative. Now, let's divide each place value:

1. Start with 6 ÷ 2 = 3 (no remainder)
2. Move to the tenths: 4 ÷ 2 = 2 (no remainder)
3. Next, the hundredths: 8 ÷ 2 = 4 (no remainder)
4. Finally, the thousandths: 2 ÷ 2 = 1 (no remainder)

Putting it all together, we get -3.241 as our final answer. See how breaking it down by place value makes the calculation more manageable?

This mental math technique for dividing decimals by integers is incredibly useful in everyday situations. Whether you're calculating discounts while shopping, splitting a bill at a restaurant, or working on more complex math problems, this method can save you time and reduce your reliance on calculators.

Remember, practice makes perfect when it comes to mental math. Start with simple problems and gradually work your way up to more complex ones. With time and practice, you'll find yourself performing these calculations with ease and confidence. Don't be discouraged if it feels challenging at first mental math is a skill that improves with regular use.

As you become more comfortable with this technique, you'll notice that it not only speeds up your calculations but also deepens your understanding of place value and the relationships between numbers. This enhanced number sense will serve you well in all areas of mathematics and everyday problem-solving.

So, the next time you encounter a decimal division problem, give this mental math method a try. You might be surprised at how quickly you can arrive at the answer without reaching for a calculator. Happy calculating!

Regrouping in Decimal Division

Regrouping in decimal division is a crucial concept that helps students accurately perform calculations involving decimals. This process is similar to regrouping in whole number division but requires extra attention to place value and decimal points. Let's explore this concept using the example 0.535 ÷ (-5) and compare it to regrouping in multiplication.

When dividing decimals, we often need to regroup or rearrange the numbers to make the division process easier. In our example, 0.535 ÷ (-5), we first need to consider the placement of the decimal point and ensure we have enough whole numbers to begin dividing.

Here are the steps to regroup and solve 0.535 ÷ (-5):

1. Identify the divisor and dividend: The divisor is -5, and the dividend is 0.535.
2. Make the divisor a whole number: In this case, -5 is already a whole number, so no change is needed.
3. Move the decimal point in both numbers: Since the divisor is already a whole number, we don't need to move its decimal point. For the dividend, we'll move the decimal point three places to the right, making it 535. Remember to move the decimal point in the quotient as well.
4. Rewrite the problem: Our new problem becomes 535 ÷ (-5).
5. Perform the division: Divide 535 by -5, keeping in mind the negative sign.
6. Place the decimal point in the quotient: Move the decimal point three places to the left in the answer, matching the movement in step 3.

The final answer will be -0.107, as 535 ÷ (-5) = -107, and we move the decimal point three places to the left.

Comparing this process to regrouping in multiplication, we can see some similarities and differences:

• Similarities:
  • Both processes involve rearranging numbers to make calculations easier.
  • Place value is crucial in both regrouping methods.
  • The concept of "borrowing" or "carrying" is present in both operations.
• Differences:
  • In multiplication, regrouping typically involves carrying digits to the left, while in division, we often move decimal points to the right.
  • Division regrouping focuses on making the divisor a whole number, whereas multiplication regrouping deals with place value within the factors.
  • The placement of the decimal point in the final answer differs between the two operations.

Understanding regrouping in decimal division is essential for students to perform accurate calculations and solve real-world problems involving decimals. By breaking down the process into clear steps and comparing it to familiar concepts like regrouping in multiplication, students can better grasp this important mathematical skill.

Remember, practice is key to mastering regrouping in decimal division. Encourage students to work through various examples, gradually increasing in complexity, to build confidence and proficiency in this fundamental mathematical operation.

Using Block Models for Decimal Division

Block models are fantastic visual tools that can help you understand and solve dividing decimals with block models. These models provide a concrete representation of abstract mathematical concepts, making it easier to grasp the process of understanding decimal division. In this guide, we'll explore two types of block models: the 100 block for hundredths and the 1000 cube for thousandths. Let's dive in and learn how to use these visual aids to tackle decimal division with confidence!

First, let's talk about the 100 block model. This model is perfect for working with decimals up to hundredths. Imagine a square divided into 100 equal parts, with 10 rows and 10 columns. Each small square represents 0.01 or one-hundredth. This visual representation helps you see how decimals relate to whole numbers and fractions.

To use the 100 block model, follow these steps:

1. Shade in the area that represents your decimal number.
2. Divide the shaded area into equal parts based on your divisor.
3. Count how many parts you have to find your quotient.

Let's try an example: 2.4 ÷ 2

1. Shade in 2.4 on your 100 block. This means shading 2 whole blocks and 4 small squares in the third row.
2. Divide this shaded area into 2 equal parts (because we're dividing by 2).
3. Count how many whole blocks and small squares are in one part. You'll find that each part has 1 whole block and 2 small squares.
4. Therefore, 2.4 ÷ 2 = 1.2

Now, let's move on to the 1000 cube model. This model is useful when working with decimals up to thousandths. Picture a large cube divided into 1000 smaller cubes, with 10 layers of 100 cubes each. Each small cube represents 0.001 or one-thousandth.

To use the 1000 cube model, follow these steps:

1. Highlight the number of cubes that represent your decimal number.
2. Divide these highlighted cubes into equal groups based on your divisor.
3. Count the number of cubes in one group to find your quotient.

Let's try another example: 0.448 ÷ 4

1. Highlight 448 small cubes in your 1000 cube model.
2. Divide these 448 cubes into 4 equal groups.
3. Count the number of cubes in one group. You'll find that each group has 112 cubes.
4. Therefore, 0.448 ÷ 4 = 0.112

Using dividing decimals with block models offers several benefits:

1. Visual representation: It helps you "see" the division process, making it easier to understand.
2. Concrete to abstract: Block models bridge the gap between concrete objects and abstract mathematical concepts.
3. Error prevention: By physically dividing the blocks, you're less likely to make calculation errors.
4. Conceptual understanding: It reinforces the concept of division as equal sharing or grouping.

Remember, practice makes perfect! The more you use these block models, the more comfortable you'll become with understanding decimal division. Don't be afraid to draw out these models on paper or use online interactive versions to help you solve problems.

As you gain confidence, you'll find that you can solve decimal division problems more quickly and accurately. Block models are an excellent stepping stone to understanding the algorithm for decimal division, which you'll learn as you progress in your math journey.

So, the next time you're faced with a tricky decimal division problem, try using a block model. Whether it's the 100 block for hundredths or the 1000 cube for thousandths, these visual aids can make a significant difference in your comprehension and accuracy.

Long Division Method for Decimals and Integers

Long division is a fundamental mathematical technique that allows us to divide larger numbers, including decimals, by integers. This method is particularly useful when dealing with complex divisions that can't be easily solved mentally. Today, we'll explore how to use the long division method to divide decimals by integers, using the example 8.9 ÷ (-4) to guide us through the process step-by-step.

Before we dive into our example, let's review some key points about dividing decimals by integers:

1. The decimal point in the quotient (answer) should be directly above the decimal point in the dividend (the number being divided).
2. When dividing by a negative number, the quotient will have the opposite sign of the dividend.
3. We can treat the division as if both numbers were positive and then adjust the sign of the final answer.

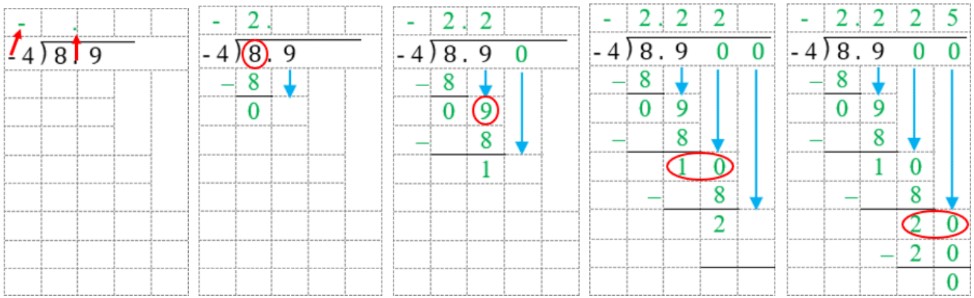
Now, let's walk through the process of solving 8.9 ÷ (-4) using long division:

1. Set up the division problem:
   • Write -4 outside the division bracket and 8.9 inside.
   • Place a decimal point above the division bracket, directly over the decimal point in 8.9.
2. Divide the first digit (8) by 4:
   • 8 ÷ 4 = 2
   • Write 2 above the division bracket.
3. Multiply and subtract:
   • Multiply 2 by 4: 2 × 4 = 8
   • Write 8 under the 8 in 8.9
   • Subtract: 8 - 8 = 0
4. Bring down the next digit:
   • Bring down the 9 from 8.9
   • We now have 9 as our new dividend
5. Divide 9 by 4:
   • 9 ÷ 4 = 2 remainder 1
   • Write 2 after the decimal point in the quotient
6. Multiply and subtract again:
   • Multiply 2 by 4: 2 × 4 = 8
   • Subtract: 9 - 8 = 1
7. The remainder is 1, which is less than the divisor (4), so we've completed the division.
8. Our quotient is 2.2, but remember we're dividing by a negative number.
9. The final answer is -2.2, as the quotient has the opposite sign of the dividend when dividing by a negative number.

To summarize, when using the long division method for decimals divided by integers:

• Align the decimal points in the dividend and quotient.
• Perform the division as if working with whole numbers.
• Bring down decimal digits as needed.
• Continue dividing until you reach a remainder smaller than the divisor or until the desired level of precision is achieved.
• If dividing by a negative number, change the sign of the final quotient.

Remember, practice long division makes perfect when it comes to long division. Don't be discouraged if it takes a few attempts to master the process. With time and patience, you'll find that dividing decimals by integers becomes second nature.

Conclusion and Practice Recommendations

In summary, we've explored three essential methods for dividing decimals by integers: the standard algorithm, the decimal point movement technique, and the fraction conversion approach. Understanding these division methods is crucial for mastering decimal operations. Each method offers unique advantages, catering to different problem types and personal preferences. To solidify your skills, it's vital to practice with a variety of examples, gradually increasing in complexity. Remember to revisit the introductory video for visual reinforcement of these concepts. As you continue your mathematical journey, challenge yourself with more advanced problems and seek out additional resources to deepen your understanding. Consider creating a study group or using online forums to discuss challenging questions. By consistently applying these methods and engaging with the material, you'll develop a strong foundation in dividing decimals by integers, paving the way for success in more advanced mathematical topics. Keep practicing, stay curious, and don't hesitate to explore further learning opportunities in this fascinating area of mathematics.